My solutions to the International Physics Olympiad: The Physics of Black Holes, IPhO Iran 2007

ZPhysics

13 Jan 202125:03

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, the host delves into the physics of black holes, focusing on the 'no hair theorem' and the event horizon's properties. Using dimensional analysis, the video demonstrates how the area of the event horizon relates to a black hole's mass, the speed of light, and the gravitational constant. It further explores the connection between black hole entropy and the second law of thermodynamics, leading to the derivation of an equation for the entropy of a black hole using fundamental constants. The video promises to continue the exploration of this topic in subsequent installments, including the discussion of Hawking radiation.

Takeaways

🧪 The video continues solving problems from the 2007 International Physics Olympiad, specifically focusing on the physics of black holes.
📏 Part one covered dimensional analysis, and part two dives into the properties of black holes, particularly the event horizon, using the no-hair theorem.
🔍 The event horizon's area is calculated using dimensional analysis, involving constants like the gravitational constant (G), the speed of light (c), and the black hole's mass (m).
⚖️ The equation derived for the event horizon's area is A = G² * m² / c⁴.
🌌 The discussion connects the area of a black hole's event horizon to its mass, drawing parallels to the second law of thermodynamics, where entropy increases.
🔥 The video explains how entropy is proposed to be proportional to the area of a black hole's event horizon, using the thermodynamic definition of entropy (S).
🧩 Dimensional analysis is used again to derive the dimensions of the constant η in the black hole entropy equation, using fundamental constants such as Planck's constant (h), the speed of light (c), the gravitational constant (G), and Boltzmann's constant (k).
📝 The derived formula for η involves G raised to the power of -1, Planck's constant h, the speed of light c raised to the power of 3, and Boltzmann's constant k.
📊 A system of equations is solved to determine the coefficients in the dimensional analysis, leading to a final expression for η.
🎓 The video concludes with a promise to cover the last parts of the problem, specifically focusing on Hawking radiation in the next video.

Q & A

What is the topic of the second part of the problem discussed in the video?
-The second part of the problem discussed in the video is about the physics of black holes, specifically focusing on finding properties of black holes according to the no hair theorem.
What is the no hair theorem in the context of black holes?
-The no hair theorem states that all the characteristics of a black hole are dependent only on its mass, meaning all other properties are irrelevant.
What does the term 'event horizon' refer to in the context of black holes?
-The event horizon is the boundary of a black hole, which is the point of no return where nothing, not even light, can escape the black hole's gravitational pull.
How is the area of the event horizon of a black hole related to its mass?
-The area of the event horizon is dependent on the mass of the black hole, the speed of light, and the universal constant of gravitation, as derived through dimensional analysis.
What is the significance of the equation A = k * (G * M^2) / (c^4) in the context of black holes?
-This equation represents the area of the event horizon of a black hole, where A is the area, G is the gravitational constant, M is the mass of the black hole, and c is the speed of light. It shows that the area is proportional to the square of the black hole's mass.
What does the video suggest about the relationship between the area of a black hole's event horizon and the second law of thermodynamics?
-The video suggests that the area of a black hole's event horizon can only increase, which is analogous to the second law of thermodynamics stating that entropy can only increase in all physical processes.
What is the significance of the Beckenstein conjecture mentioned in the video?
-The Beckenstein conjecture proposes that the entropy of a black hole is proportional to the area of its event horizon, making it a key concept in understanding the thermodynamics of black holes.
What is the thermodynamic definition of entropy used in the video?
-The thermodynamic definition of entropy used in the video is DS = Q / T, where DS is the change in entropy, Q is the heat transferred, and T is the temperature.
How does the video use dimensional analysis to derive the expression for the black hole entropy factor eta?
-The video uses dimensional analysis to equate the dimensions of entropy to the dimensions of the fundamental constants G, h, c, and k, and then solves for the coefficients to derive the expression for eta.
What is the final expression for eta derived in the video?
-The final expression for eta derived in the video is eta = (k * c^3) / (G * h), where k is the Boltzmann constant, c is the speed of light, G is the gravitational constant, and h is Planck's constant.
What does the video suggest about the next topic to be discussed in the series?
-The video suggests that the next topic to be discussed in the series will be about the famous Hawking radiation, which is another important aspect of black hole physics.

Outlines

00:00

🌌 Introduction to Black Hole Physics and No Hair Theorem

The video script begins with an introduction to the topic of black holes, specifically focusing on the 'no hair theorem' which states that the properties of a black hole are determined solely by its mass. The speaker discusses the event horizon and how to calculate its area using dimensional analysis. The script mentions the fundamental constants of physics—gravitational constant (G), speed of light (c), and mass of the black hole (m)—and their roles in determining the area of the event horizon. The speaker also references previous work on dimensional analysis from an earlier video, encouraging viewers to review it for a deeper understanding.

05:01

🔍 Dimensional Analysis of the Event Horizon Area

This paragraph delves into the application of dimensional analysis to derive the formula for the area of a black hole's event horizon. The speaker sets up a system of equations based on the dimensions of length, mass, and time to find the exponents (alpha, beta, and gamma) for the constants G, c, and m. Through a series of substitutions and simplifications, the speaker solves for these exponents, revealing that the area of the event horizon is proportional to the square of the black hole's mass, divided by the speed of light raised to the fourth power.

10:03

🌡 Entropy and the Second Law of Thermodynamics

The script moves on to discuss the concept of entropy in relation to black holes, drawing an analogy with the second law of thermodynamics which states that entropy can only increase. The speaker introduces the idea that the area of a black hole's event horizon can be associated with its entropy, a hypothesis proposed by Bekenstein. The speaker then uses the thermodynamic definition of entropy (ds = dq/T) to establish the dimensions of entropy and sets up another round of dimensional analysis to express the dimension constant eta in terms of fundamental constants h, c, G, and k.

15:03

🔧 Solving for the Entropy Constant of a Black Hole

In this section, the speaker continues the dimensional analysis to solve for the constant eta, which is used to calculate the entropy of a black hole. The speaker formulates a system of equations based on the dimensions of the fundamental constants and their powers. Through a process of elimination and substitution, the speaker finds the values for the coefficients, which are then used to express eta in terms of G, h, c, and k. The resulting formula for eta is presented, showing the relationship between the constants and the entropy of a black hole.

20:05

🌟 Conclusion and Preview of Upcoming Content

The final paragraph wraps up the current discussion on black hole entropy and dimensional analysis, celebrating the successful derivation of the formula for eta. The speaker thanks the viewers for their engagement with the complex mathematical content and encourages them to subscribe and like the video if they found it useful. The script ends with a teaser for the next video, which will cover the remaining parts of the problem, including the famous Hawking radiation.

Mindmap

Keywords

💡Dimensional Analysis

Dimensional analysis is a mathematical technique used to deduce or verify physical relationships by comparing the dimensions of the quantities involved. In the video, dimensional analysis is applied to derive the formula for the area of a black hole's event horizon and the entropy constant η. This method helps in identifying the powers of physical constants (like gravitational constant, speed of light) that influence the properties of a black hole.

💡Event Horizon

The event horizon is the boundary surrounding a black hole beyond which nothing, not even light, can escape. In the video, the area of the event horizon is discussed as a function of the black hole's mass, gravitational constant, and the speed of light. This concept is central to understanding black hole physics, as it defines the 'point of no return' for objects approaching the black hole.

💡No Hair Theorem

The No Hair Theorem in physics asserts that all black holes can be completely described by just three externally observable parameters: mass, electric charge, and angular momentum. The video uses this theorem to explain that the characteristics of a black hole, like its event horizon, depend solely on its mass, which is crucial for simplifying the complex nature of black holes into manageable calculations.

💡Gravitational Constant (G)

The gravitational constant (G) is a fundamental constant in physics that quantifies the strength of gravity in the universal law of gravitation. In the video, G is used in the dimensional analysis to derive the area of a black hole's event horizon and the entropy factor η. It plays a critical role in determining the scale of gravitational effects in black holes.

💡Entropy

Entropy is a measure of disorder or randomness in a system, often associated with the second law of thermodynamics, which states that entropy always increases. The video relates the concept of entropy to black holes, where the area of the event horizon is proportional to the black hole's entropy, reflecting the irreversible nature of black hole growth.

💡Planck's Constant (h)

Planck's constant (h) is a fundamental constant in quantum mechanics that relates the energy of a photon to its frequency. In the video, h is part of the dimensional analysis to determine the constant η in the entropy formula for black holes. It signifies the quantum mechanical aspects of black hole thermodynamics.

💡Speed of Light (c)

The speed of light (c) is a universal constant representing the speed at which light travels in a vacuum. In the video, c is a crucial factor in the dimensional analysis used to calculate both the area of the event horizon and the entropy of a black hole. The speed of light is fundamental in the equations governing relativity and black hole physics.

💡Boltzmann's Constant (k)

Boltzmann's constant (k) is a physical constant that relates the average kinetic energy of particles in a gas with the temperature of the gas. In the video, k appears in the dimensional analysis to find the entropy constant η, linking thermodynamic properties with the statistical mechanics of black holes. This constant is vital in connecting macroscopic and microscopic physical laws.

💡Hawking Radiation

Hawking Radiation is theoretical radiation predicted to be emitted by black holes due to quantum effects near the event horizon. The video mentions it as a topic to be covered in a subsequent part of the problem, indicating its importance in understanding black hole thermodynamics and the eventual evaporation of black holes.

💡System of Equations

A system of equations is a set of equations with multiple variables that are solved simultaneously to find a common solution. In the video, a system of equations is derived from the dimensional analysis to find the exponents of physical constants like G, h, c, and k, which contribute to determining the area of a black hole's event horizon and its entropy.

Highlights

Introduction to the continuation of solutions for the 2007 International Physics Olympiad problem on black holes.

Exploration of the 'no hair theorem' which states that the characteristics of a black hole depend solely on its mass.

Dimensional analysis to determine the properties of black holes, specifically the area of the event horizon.

Derivation of the equation for the area of the event horizon using fundamental constants: gravitational constant (G), speed of light (c), and mass (m).

Solving a system of equations to find the exponents alpha, beta, and gamma for the area of the event horizon.

Result showing that the area of the event horizon is proportional to the square of the black hole's mass and inversely proportional to the speed of light squared.

Connection between the increase of a black hole's event horizon area and the second law of thermodynamics, implying that entropy can only increase.

Beckenstein's proposal to assign entropy to a black hole proportional to the area of its event horizon.

Dimensional analysis to determine the dimensions of entropy using the thermodynamic definition of entropy (ds = dq/T).

Expression of the dimension constant eta as a function of fundamental constants h, c, g, and k.

Derivation of the entropy of a black hole using dimensional analysis and fundamental constants.

Solution of a system of equations to find the coefficients for eta in the black hole entropy equation.

Final equation for eta, the factor in the black hole entropy equation, derived using dimensional analysis.

Conclusion of the video with an invitation to the next part of the problem concerning Hawking radiation.

Overall achievement of using dimensional analysis to derive important formulas related to black holes, showcasing the method's power.

Transcripts

Browse More Related Video

Deriving Hawking's most famous equation: What is the temperature of a black hole?

Lecture 4 | Topics in String Theory

Lecture 2 | Topics in String Theory

Lecture 6 | Topics in String Theory

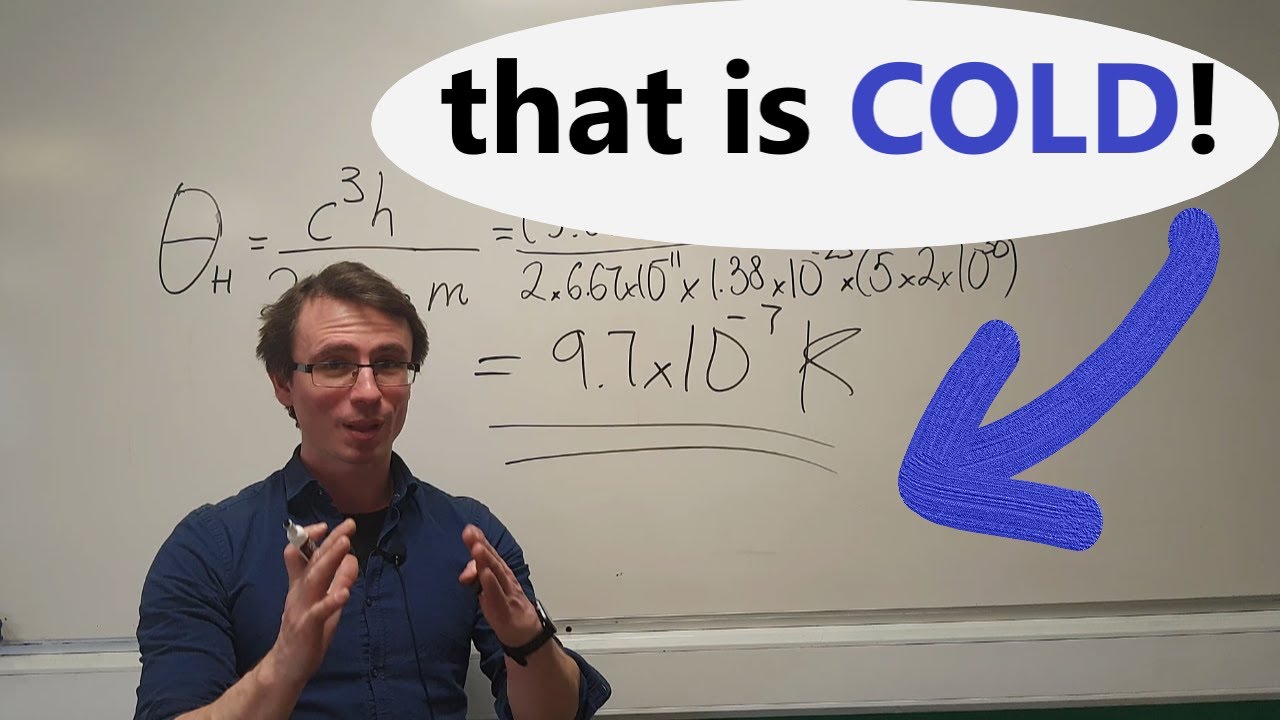
What is the Hawking temperature of a black hole? IPhO Problem

How to Make Black Holes (Both Regular and Supermassive)

Related Tags

Black Holes Dimensional Analysis Physics Olympiad Event Horizon No Hair Theorem Entropy Beckenstein Thermodynamics Hawking Radiation Fundamental Constants