LAST Problem from the International Physics Olympiad
TLDRThis script tackles the intriguing problem of a black hole's mass change rate in the context of the universe, considering both Hawking radiation and cosmic microwave background radiation. It explains the application of fundamental physics constants and Stefan-Boltzmann's law to derive the rate of mass change. The script further explores the concept of thermal equilibrium for black holes, revealing a fascinating symmetry where the black hole's temperature matches the cosmic microwave background temperature at equilibrium. The explanation is rich with mathematical derivations, showcasing the beauty of physics in understanding the cosmos.
Takeaways
- 📚 The script discusses a problem from the International Physics Olympiad related to black holes and their interaction with cosmic microwave background radiation.
- 🌡️ The Hawking temperature of a black hole is derived using fundamental constants and the area of the event horizon, which is related to the black hole's mass.
- ⚫ The black hole is considered as part of the universe, receiving cosmic microwave background radiation, which contributes to its mass.
- 🌌 The cosmic microwave background radiation has a temperature of approximately 2.7 Kelvin and affects the black hole's mass.
- 🔢 The rate of change of the black hole's mass is calculated by considering the difference between the power emitted due to Hawking radiation and the power absorbed from cosmic microwave background radiation.
- ℎ The use of Einstein's mass-energy equivalence principle (E=mc²) simplifies the calculation of the rate of change of mass.
- 🔄 Stefan-Boltzmann's law is applied to find the power emitted by the black hole due to Hawking radiation and the power absorbed from the cosmic microwave background.
- 🧮 The algebraic manipulation of the equations leads to an expression for the rate of change of the black hole's mass in terms of fundamental constants and the black hole's mass.
- ⭐ The black hole reaches thermal equilibrium when the rate of change of its mass is zero, which is derived by setting the derivative equal to zero and solving for the mass.
- 🌡️ At thermal equilibrium, the temperature of the black hole is found to be equal to the temperature of the cosmic microwave background radiation.
- 🤔 The script ends with a hint to explore the derivation of the temperature of a black hole, suggesting a deeper understanding of Hawking radiation.
Q & A
What is the topic of the discussion in the provided script?
-The topic of the discussion is the calculation of the rate of change of a black hole's mass considering both Hawking radiation and the absorption of cosmic microwave background radiation.
What is the Hawking temperature of a black hole?
-The Hawking temperature of a black hole is a theoretical temperature at which black holes emit radiation due to quantum effects near the event horizon. It is given by an expression involving fundamental constants such as the Planck constant, the speed of light, and the gravitational constant.
What is the significance of Stefan Boltzmann's constant in this context?
-Stefan Boltzmann's constant is used to describe the power emitted by a black hole due to Hawking radiation, which is proportional to the fourth power of the temperature and the surface area of the black hole.
What is the role of the cosmic microwave background radiation in the black hole's mass change?
-The cosmic microwave background radiation contributes to the mass of the black hole by being absorbed, which counteracts the mass loss due to Hawking radiation.
How does the black hole's mass change over time?
-The black hole's mass changes over time due to the difference between the power emitted as Hawking radiation and the power absorbed from the cosmic microwave background radiation.
What is the relationship between the rate of change of energy and the rate of change of mass in the context of a black hole?
-The rate of change of energy (dE/dt) is related to the rate of change of mass (dM/dt) through the equation dE/dt = c^2 * dM/dt, where c is the speed of light.
What is the significance of setting the rate of change of mass to zero?
-Setting the rate of change of mass to zero signifies the point at which the black hole is in thermal equilibrium, neither gaining nor losing mass overall.
What is the expression for the mass of a black hole at thermal equilibrium?
-The mass of a black hole at thermal equilibrium (M*) is given by an expression involving the speed of light, the Planck constant, the gravitational constant, Boltzmann's constant, and the temperature of the cosmic microwave background radiation.
What is the temperature of a black hole at thermal equilibrium?
-At thermal equilibrium, the temperature of the black hole is equal to the temperature of the cosmic microwave background radiation.
How does the derivation of the temperature of a black hole relate to the concept of Hawking radiation?
-The derivation of the temperature of a black hole is directly related to Hawking radiation, as it describes the temperature at which black holes emit this radiation due to quantum effects.
Outlines
🌌 Black Hole Mass Change Analysis
This paragraph delves into the complex dynamics of a black hole's mass change, considering it as part of the universe and its interaction with cosmic microwave background radiation. The script introduces the concept of Hawking temperature and Stefan Boltzmann's constant to calculate the rate of change of the black hole's mass. It outlines the algebraic process to determine the net energy change by considering both the emitted radiation due to Hawking and the absorbed cosmic microwave background radiation. The ultimate goal is to find the rate of change of the black hole's mass, which involves intricate calculations with fundamental constants and the area of the black hole's event horizon.
🔭 Thermal Equilibrium of Black Holes
The second paragraph continues the exploration of black hole physics by examining the scenario where a black hole reaches thermal equilibrium with the cosmic microwave background radiation. It discusses the condition where the rate of mass change of the black hole becomes zero, leading to a state of balance between the radiation emitted due to Hawking temperature and the radiation absorbed from the background. The script provides a mathematical derivation to find the mass of the black hole at this equilibrium and reveals an intriguing result: the black hole's temperature matches the temperature of the background radiation. This section also touches upon the derivation of the temperature of a black hole, hinting at the profound implications of Hawking radiation.
Mindmap
Keywords
💡Hawking Temperature
💡Stefan-Boltzmann Constant
💡Event Horizon
💡Cosmic Microwave Background Radiation
💡Einstein's Mass-Energy Equivalence
💡Thermal Equilibrium
💡Black Hole Mass
💡Hawking Radiation
💡Planck Constant
💡Boltzmann Constant
💡Gravitational Constant
Highlights
Solving the black hole question from the International Physics Olympiad using the Hawking temperature formula.
Hawking temperature of a black hole is derived using fundamental constants and the area of the Event Horizon.
Considering the black hole as part of the universe, receiving cosmic microwave background radiation.
The black hole's mass change rate is influenced by both Hawking radiation emission and cosmic microwave background radiation absorption.
Using the equation E=mc^2 to relate the rate of change of energy to the rate of change of mass.
Applying Stefan-Boltzmann's law to calculate the power output due to Hawking radiation.
Deriving an algebraic expression for the rate of change of mass (dM/dt) in terms of fundamental constants.
The expression for dM/dt includes terms for both the emitted power due to Hawking radiation and the absorbed power from cosmic microwave background.
Simplifying the expression to isolate the rate of change of mass, showing a balance between emitted and absorbed power.
Setting the derivative equal to zero to find the black hole's mass at thermal equilibrium.
Rearranging the equation to solve for the mass of the black hole at thermal equilibrium (M*).
Finding an expression for M* that includes the cosmic microwave background temperature.
Demonstrating that at thermal equilibrium, the black hole's temperature equals the cosmic microwave background temperature.
The derivation of the temperature of a black hole at thermal equilibrium from the mass expression.
The surprising result that the black hole's temperature matches the cosmic microwave background temperature at equilibrium.
The importance of understanding the derivation of Hawking radiation for the temperature of a black hole.
The significance of the theoretical contribution to the understanding of black hole thermodynamics.
Transcripts
Browse More Related Video

HAWKING Radiation Physics Olympiad Problem

Cosmology Lecture 7

My solutions to the International Physics Olympiad: The Physics of Black Holes, IPhO Iran 2007
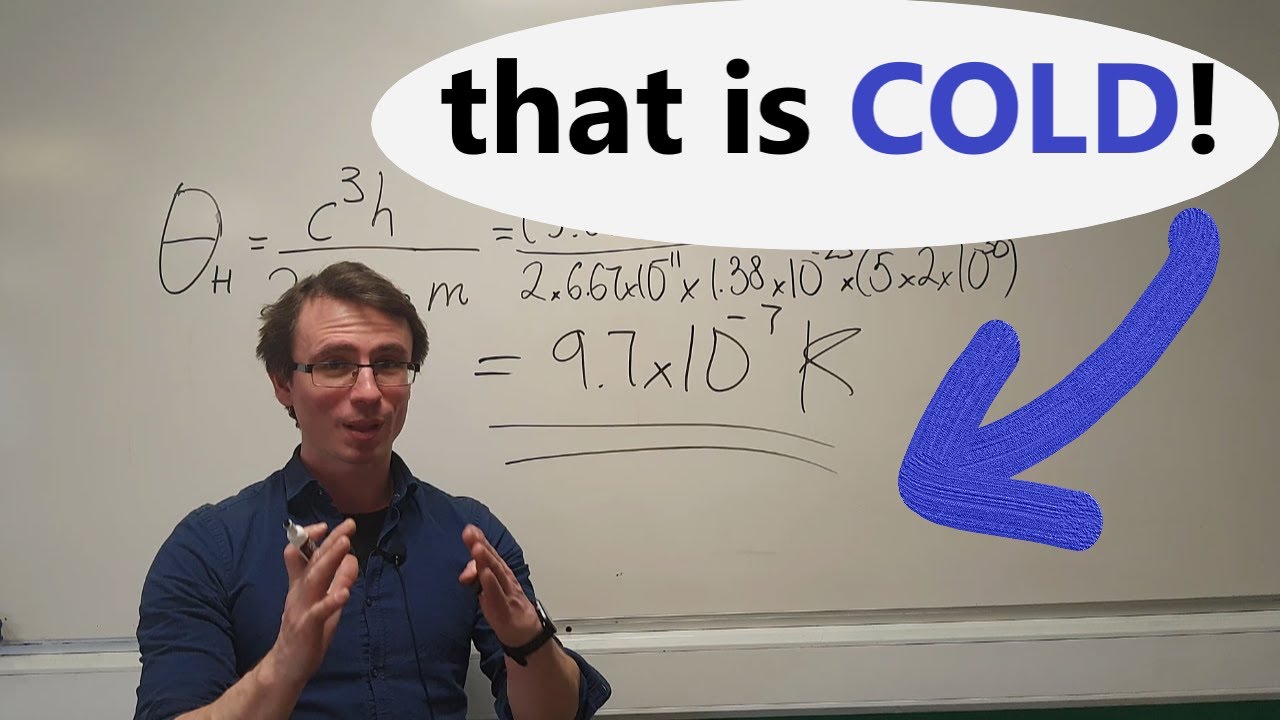
What is the Hawking temperature of a black hole? IPhO Problem

Deriving Hawking's most famous equation: What is the temperature of a black hole?

Black Holes - An Introduction
5.0 / 5 (0 votes)
Thanks for rating: