AP Physics 1 - Simple Harmonic Motion

Dan Fullerton
22 Oct 201307:42
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces simple harmonic motion (SHM), a fundamental concept in physics where an object oscillates under the influence of a restoring force. It explains the conditions for SHM, the relationship between displacement, frequency, and period, and how to identify extrema and zeros in displacement, velocity, and acceleration. The script uses examples like a mass on a spring and a pendulum to illustrate SHM and draws parallels with uniform circular motion. It also solves a sample problem to demonstrate how to calculate an object's position and velocity in SHM.

Takeaways
  • πŸ“š Simple Harmonic Motion (SHM) is a periodic oscillating motion where a displaced object is subject to a restoring force directly proportional to the displacement.
  • πŸ“ˆ The displacement in SHM can be expressed as a cosine or sine function of time, in the form of a cos(Omega t) or a sin(Omega t), where a is the amplitude, Omega is the angular frequency, and t is time.
  • πŸ”„ The relationship between frequency (f), angular frequency (Omega), and period (T) is given by Omega = 2pi f and T = 2pi/Omega.
  • πŸ“Š The maximum velocity (v_max) of an object in SHM is Omega a, and the maximum acceleration (a_max) is Omega^2 a.
  • 🌐 Examples of SHM include a mass on a spring, a pendulum, a tree limb after disturbance, and even atomic vibrations in solids.
  • πŸ”— SHM is closely related to uniform circular motion, with the horizontal motion of an object in uniform circular motion mirroring the SHM of an object attached to a spring.
  • πŸ“Œ The phase angle (phi) in the SHM equation x = a cos(Omega t + phi) or x = a sin(Omega t + phi) indicates the starting point of the motion.
  • πŸ”’ To solve for an object's position in SHM, use the general form x = a cos(Omega t) and substitute the given values of amplitude, angular frequency, and time.
  • ⏱️ The time when the object is at a specific position can be found by solving cos(Omega t) = x/a for t, using the inverse cosine function.
  • πŸ“ˆ The script provides a sample problem where an object is released from a maximum displacement of 0.2 meters and makes 60 oscillations in one minute, with solutions for angular frequency, position at a specific time, and time at a specific position.
  • 🌟 SHM is a fundamental concept in physics, applicable in various fields, and understanding its principles and formulas is essential for further studies in the subject.
Q & A

  • What is simple harmonic motion?

    -Simple harmonic motion is a type of periodic oscillating motion where the restoring force on an object is directly proportional to its displacement from an equilibrium position.

  • What are the conditions necessary for simple harmonic motion?

    -Simple harmonic motion occurs when an object is subject to a restoring force that is linearly related to its displacement from an equilibrium position.

  • How is simple harmonic motion represented mathematically?

    -Simple harmonic motion can be represented by an equation of the form x = a*cos(Ο‰*t + Ο†) or x = a*sin(Ο‰*t + Ο†), where x is the displacement, a is the amplitude, Ο‰ is the angular frequency, t is time, and Ο† is the phase angle.

  • What is the relationship between frequency, angular frequency, and period?

    -The angular frequency (Ο‰) is related to the frequency (f) and period (T) by the equation Ο‰ = 2Ο€f = 2Ο€/T.

  • What are the maximum displacement, velocity, and acceleration of an object in simple harmonic motion?

    -The maximum displacement is equal to the amplitude (a). The maximum velocity is given by v = Ο‰*a, and the maximum acceleration is a = Ο‰^2*a.

  • How is simple harmonic motion related to uniform circular motion?

    -Simple harmonic motion and uniform circular motion are related in that the x and y positions in uniform circular motion can be described by cosine and sine functions, respectively, similar to the displacement function in simple harmonic motion.

  • What are some real-world examples of simple harmonic motion?

    -Examples of simple harmonic motion include a pendulum swinging, a tree limb vibrating after being disturbed, a child on a swing, and even the vibration of atoms in solids.

  • How can the phase angle be determined in the equation of simple harmonic motion?

    -The phase angle (Ο†) in the equation of simple harmonic motion is determined by the initial conditions of the motion, specifically the starting position and the time at which the motion begins.

  • What happens to the object's position at time T equals 10 seconds in the given sample problem?

    -At time T equals 10 seconds, the object is at its equilibrium position, x equals 0.2 meters, since the cosine of 2Ο€ times 10 seconds (which is a full cycle) is 1.

  • How can you find the time when the object is at position x equals 0.1 meter in the given sample problem?

    -To find the time when the object is at x equals 0.1 meter, you set up the equation cos(Ο‰*T) = x/a, solve for T using the inverse cosine function, and substitute the values of x, a, and Ο‰. In this case, T equals the inverse cosine of 0.1/0.2 divided by 2Ο€, which gives a time of approximately 0.167 seconds.

  • How many oscillations does the object in the sample problem make in one minute?

    -The object in the sample problem makes 60 complete oscillations in one minute, which corresponds to a frequency of 1 Hertz.

Outlines
00:00
πŸ“š Introduction to Simple Harmonic Motion

This paragraph introduces the concept of simple harmonic motion (SHM), explaining its conditions and how it manifests in nature. It outlines the objectives of the lesson, which include understanding the restoring force behind SHM, expressing displacement using cosine or sine functions, and identifying key characteristics of motion such as maxima, minima, and zeros for displacement, velocity, and acceleration. Examples of SHM in everyday life, like a pendulum or a vibrating tree branch, are provided to illustrate the concept. The relationship between SHM and uniform circular motion is also discussed, highlighting how the two are closely linked through angular displacement and frequency.

05:02
πŸ”’ Mathematical Analysis of Simple Harmonic Motion

This paragraph delves into the mathematical aspects of simple harmonic motion. It begins by calculating the angular frequency and using it to express the object's position as a function of time. The general equation for SHM is presented, and the phase angle's role in determining the starting point of the motion is explained. The maximum speed and acceleration of an object in SHM are derived from the slopes of the position-time and velocity-time curves, respectively. A sample problem is solved to demonstrate how to apply these concepts, including determining the object's position at a specific time and finding the time when the object is at a particular position.

Mindmap
Keywords
πŸ’‘Simple Harmonic Motion
Simple Harmonic Motion (SHM) is a type of periodic motion where an object moves back and forth under the influence of a restoring force that is directly proportional to the displacement from its equilibrium position. In the video, SHM is described as a common phenomenon in nature, such as a pendulum swinging or a tree branch vibrating. It is also related to uniform circular motion, where the horizontal motion of an object in a circle is mirrored on a frictionless surface.
πŸ’‘Displacement
Displacement refers to the change in position of an object from its original point. In the context of SHM, displacement is used to describe how far an object is from its equilibrium position, typically represented by a cosine or sine function of time. The video explains that the displacement can be expressed in the form of a cosine Omega T or a sine Omega T, which helps in describing the motion of the object undergoing SHM.
πŸ’‘Restoring Force
A restoring force is a force that acts to return an object to its equilibrium position. In SHM, the restoring force is directly proportional to the displacement, which is a defining characteristic of this type of motion. For example, in a spring-mass system, the restoring force is provided by the spring's tension, which pulls the mass back to its equilibrium position when it is stretched or compressed.
πŸ’‘Frequency
Frequency is the number of complete oscillations or cycles that occur in a unit of time. In the video, it is mentioned that the frequency of an object undergoing SHM is 1 Hertz, which means it completes one cycle per second. The relationship between frequency, period, and angular frequency is also discussed, highlighting the importance of understanding these concepts for analyzing SHM.
πŸ’‘Angular Frequency
Angular frequency, denoted by Omega, is the rate at which an object rotates or completes an angular displacement around a circle per unit of time, measured in radians per second. In SHM, angular frequency is related to the frequency of oscillation and is used to describe the time-dependent behavior of the object's displacement. The video explains that Omega is 2 pi times the frequency, which is a fundamental relationship in the analysis of SHM.
πŸ’‘Period
The period is the time it takes for an object to complete one full cycle of its motion and return to its starting position. In the context of SHM, the period is related to the object's frequency and angular frequency. The video provides an example where the object completes 60 oscillations in one minute, which corresponds to a frequency of 1 Hertz, and thus a period of one minute or 60 seconds.
πŸ’‘Maxima, Minima, and Zeros
In the context of SHM, maxima and minima refer to the maximum and minimum values of displacement, velocity, and acceleration that an object experiences during its motion. Zeros indicate the points where the object passes through the equilibrium position. The video explains how to identify these points by analyzing the position, velocity, and acceleration curves of an object undergoing SHM.
πŸ’‘Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely back and forth. In the video, a pendulum is used as an example of an object undergoing SHM. The motion of the pendulum is influenced by the gravitational force acting on the weight, which acts as a restoring force, pulling the pendulum back towards its equilibrium position.
πŸ’‘Spring-Mass System
A spring-mass system is a mechanical system consisting of a spring and a mass attached to it. When the mass is displaced from its equilibrium position and released, it oscillates back and forth in SHM. The spring's restoring force is what causes the oscillation. The video uses a spring-mass system to illustrate the principles of SHM and how the displacement of the mass can be described using cosine or sine functions.
πŸ’‘Vibration
Vibration refers to the oscillatory motion of an object around an equilibrium position. In the video, the vibration of a tree limb after it has been disturbed is given as an example of SHM. The vibration is a result of the restoring force that acts to bring the object back to its equilibrium state.
πŸ’‘Sample Problem
The video presents a sample problem involving an object undergoing SHM, which is released from a maximum displacement and completes a certain number of oscillations within a given time. The problem is used to demonstrate how to calculate the object's angular frequency, determine its position at a specific time, and find the time when the object is at a particular position. This practical application helps viewers understand how to apply the concepts of SHM to real-world scenarios.
Highlights

The lesson focuses on simple harmonic motion (SHM), a fundamental concept in physics.

SHM occurs when a displaced object is subject to a restoring force that is directly proportional to the displacement.

Examples of SHM include a pendulum swinging, a tree branch vibrating, and a child on a swing.

The relationship between SHM and uniform circular motion is discussed, highlighting their similarities.

The mathematical expression for displacement in SHM is given as a cosine or sine function of time.

The frequency, period, and angular frequency of SHM are interconnected and can be calculated using specific formulas.

The maximum displacement (amplitude) of an object in SHM can be represented by the variable 'a'.

The maximum speed and acceleration of an object in SHM are determined by the angular frequency (Omega) and amplitude (a).

A sample problem is provided to demonstrate how to calculate the angular frequency, position, and time for an object in SHM.

The object's angular frequency is calculated to be 2 pi radians per second using its frequency of 1 Hertz.

The object's position at a specific time (10 seconds) is determined to be 0.2 meters using the displacement formula.

The time at which the object reaches a position of 0.1 meter is calculated to be approximately 0.167 seconds.

The lesson emphasizes the practical applications and ubiquity of SHM in nature and everyday phenomena.

The cosine and sine functions are used to describe the motion of an object in SHM, with the phase angle (Phi) indicating the starting point of the graph.

The maximum velocity and acceleration of an object in SHM can be found by taking the slopes of the position-time and velocity-time curves, respectively.

The lesson concludes with a call to action for further exploration of SHM and an encouragement to seek additional resources for understanding.

The importance of understanding SHM is highlighted as it is a response to disturbances and is prevalent in our world.

The lesson provides a comprehensive overview of SHM, including its conditions, mathematical expressions, and key characteristics.

Transcripts

Browse More Related Video

Simple harmonic motion and angular frequency [IB Physics SL/HL]

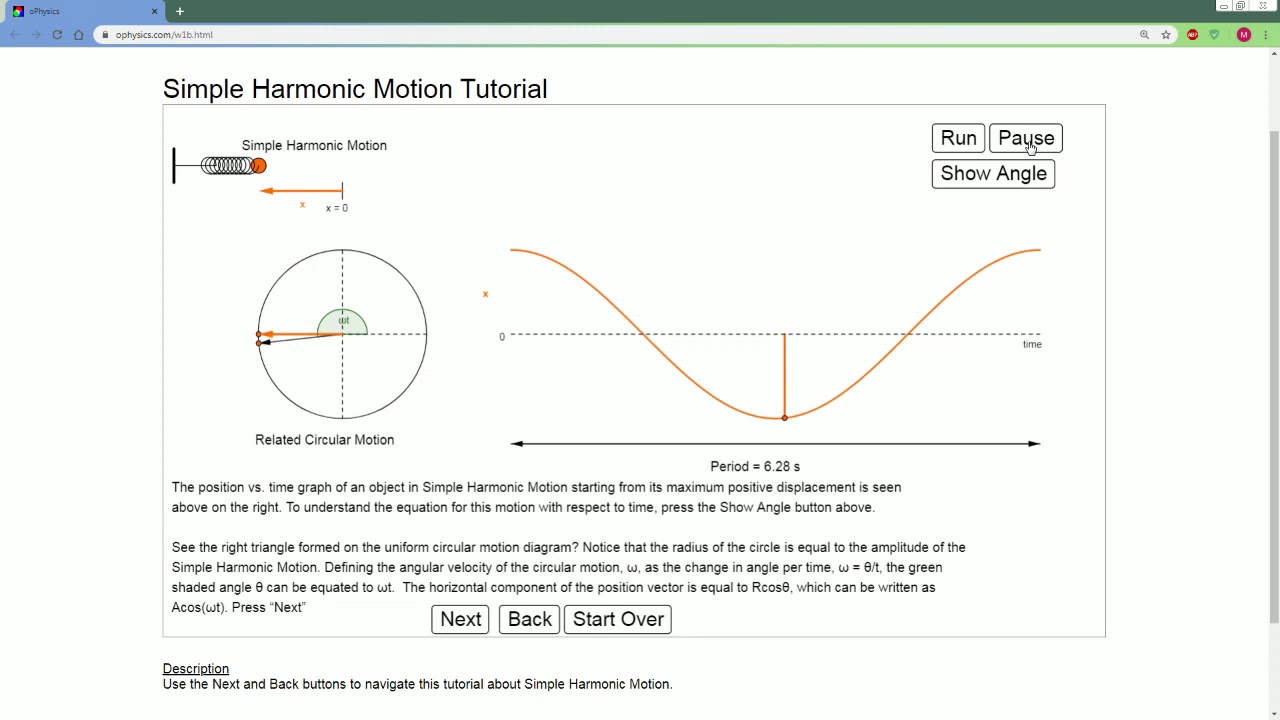
AP Physics Lecture on Simple Harmonic Motion. Watch this before 6.C

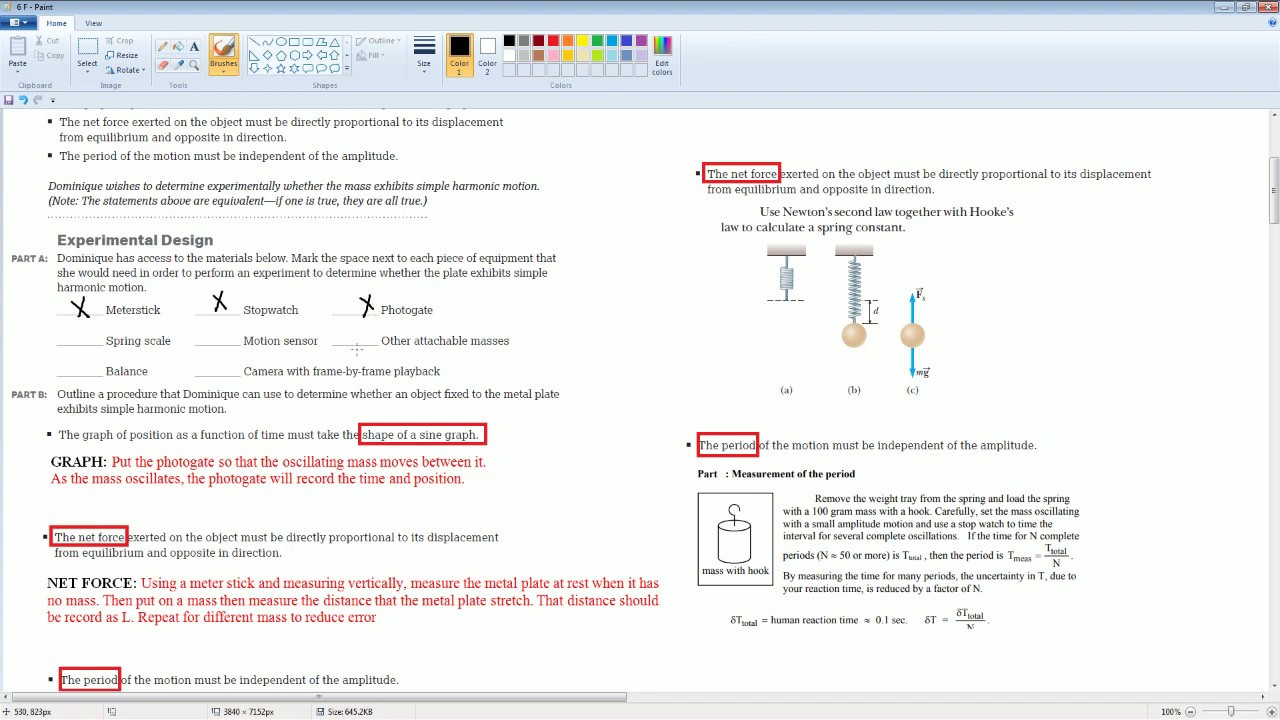
AP Physics Workbook 6.F Determining If Motion is SHM

'AP Physics 2023 Exam Solutions|Q1. PART C ( i ) | Complete Step-by-Step Answers and Explanations"

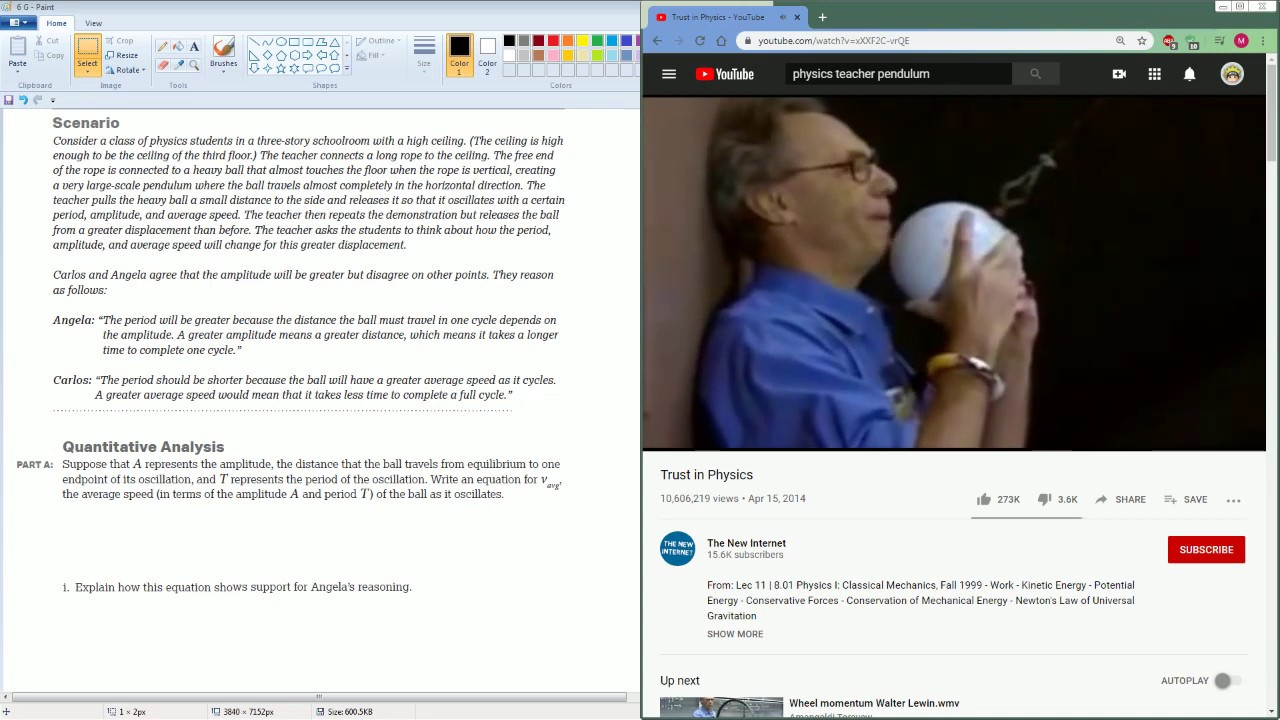
AP Physics Workbook 6.G Period and Amplitude for SHM

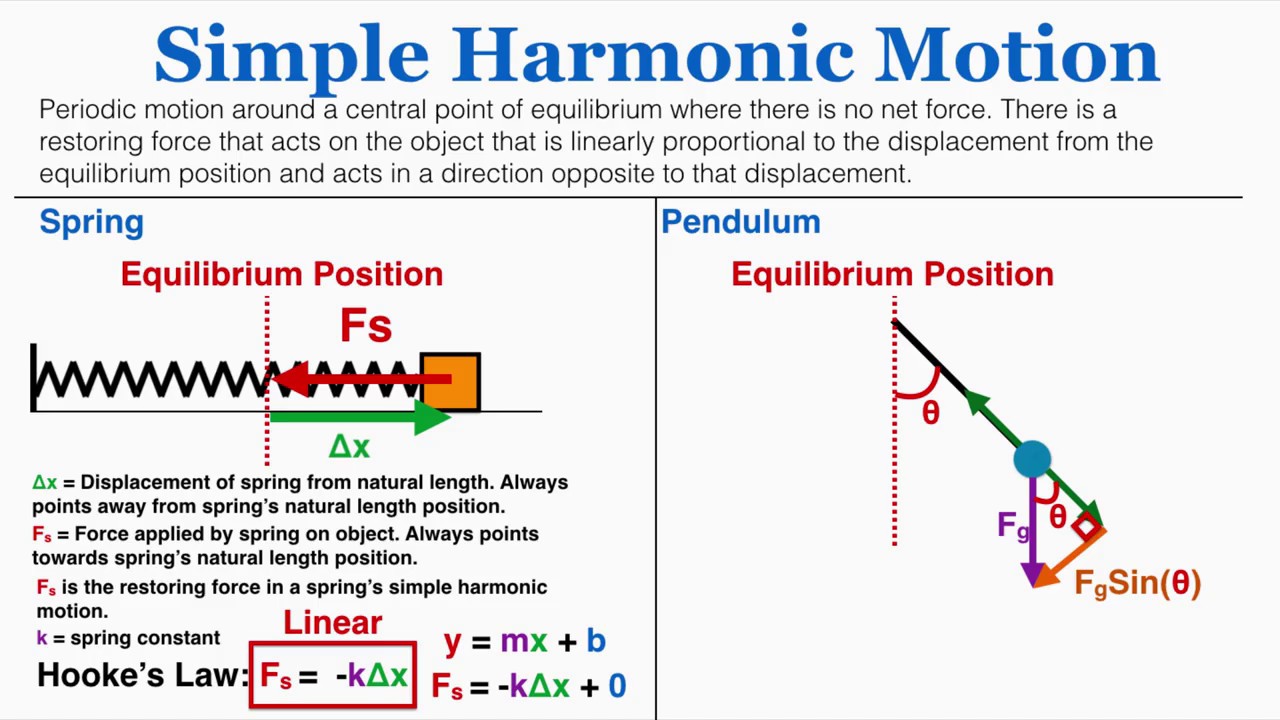
Simple Harmonic Motion - IB Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsHarmonic MotionRestoring ForcesOscillationCircular MotionMathematical ModelsMechanical WavesEducational ContentLecture SeriesDynamic Systems