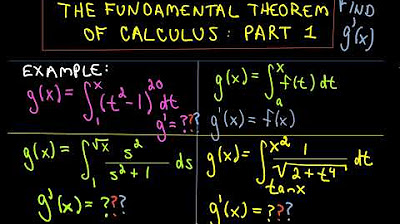The Essence of Multivariable Calculus | #SoME3
TLDRThis script explores the interconnectedness of multivariable calculus through a personal narrative, starting with the fundamental theorem of single-variable calculus and building up to the generalized Stokes' theorem. It simplifies complex concepts like gradients, curls, and divergences, illustrating how these are all forms of derivatives. The script emphasizes the unifying principle that the integral of a derivative over any shape equates to the original function evaluated along the shape's boundary, culminating in the insight that all of calculus can be seen as variations of the same fundamental idea.
Takeaways
- 📚 The script discusses the interconnectedness of various theorems in multivariable calculus, aiming to provide a unified perspective on the subject.
- 🧠 It emphasizes the difficulty many students face in seeing the relationships between individual theorems and concepts in multivariable calculus.
- 🔍 The presenter shares a personal anecdote about struggling to understand the connections between theorems, despite understanding them individually.
- 📈 The script introduces five key theorems: the Fundamental Theorem of Single Variable Calculus, the Fundamental Theorem of Line Integrals, Green's Theorem, Stokes's Theorem, and the Divergence Theorem.
- 📉 The presenter explains that understanding multivariable calculus is about gaining the right perspective, similar to how astronauts view Earth from space.
- 📝 The script provides an intuitive explanation of the Fundamental Theorem of Single Variable Calculus, breaking down the formula into its geometric components.
- 📐 It explains the concept of line integrals over a curve in the context of vector fields, and how they relate to the gradient of a multivariable function.
- 🌐 The script explores the idea that the gradient, curl, and divergence are all different forms of derivatives, which is key to understanding the theorems.
- 🔗 The presenter illustrates how theorems like Green's and Stokes's Theorem can be seen as special cases of more general theorems, leading to the Generalized Stokes's Theorem.
- 🌟 The Generalized Stokes's Theorem is presented as the culmination of the patterns observed in multivariable calculus, showing that the integral of a derivative over a shape is equal to the original function along the boundary.
- 🚀 The script concludes with the idea that higher-level mathematics reveals the underlying unity of mathematical concepts, and the importance of gaining perspective through discussion with peers.
Q & A
What is the main theme of the video script?
-The main theme of the video script is to demonstrate how various theorems in multivariable calculus are interconnected and can be understood from a unified perspective.
What is the fundamental theorem of single variable calculus?
-The fundamental theorem of single variable calculus states that the integral of a function's derivative over an interval is equal to the function's value at the endpoints of the interval.
What is the significance of the Leibniz notation in understanding derivatives?
-Leibniz notation represents the derivative as a quotient, which helps in understanding the geometric intuition behind the derivative as the slope of the tangent line to the function at a given point.
What is the fundamental theorem of line integrals?
-The fundamental theorem of line integrals states that the integral of a gradient vector field over a curve is equal to the original multivariable function evaluated at the endpoints of the curve.
What does the video script suggest about the relationship between the theorems of multivariable calculus?
-The video script suggests that all theorems of multivariable calculus can be seen as different manifestations of a single underlying principle: the integral of a derivative over a shape is equal to the original function evaluated along the boundary of that shape.
What is the purpose of the 'formulas dictionary' mentioned in the script?
-The 'formulas dictionary' is a collection of theorems and their plain English interpretations, which helps to simplify and generalize the complex mathematical concepts presented in the script.
What is the generalized Stokes' theorem mentioned at the end of the script?
-The generalized Stokes' theorem is a unifying principle that states the integral of a differential form over a boundary is equal to the integral of its exterior derivative over the whole shape, generalizing all of calculus in any number of dimensions.
How does the script describe the process of understanding multivariable calculus?
-The script describes the process as one of gaining perspective, where understanding the interconnectedness of various theorems provides a deeper and more holistic view of multivariable calculus.
What is the role of the gradient in multivariable calculus?
-The gradient is a vector field that represents the direction of the greatest rate of increase of a function, compiling all the partial derivatives of the function with respect to each input variable.
What does the script suggest as a key takeaway from the discussion on multivariable calculus?
-The key takeaway suggested by the script is the realization that all theorems in multivariable calculus can be generalized to the principle that the integral of a derivative over a shape equals the original function along the boundary of that shape.
Outlines
📚 Multivariable Calculus: A Holistic Perspective
The paragraph introduces the speaker's personal experience with multivariable calculus and the struggle to see the interconnectedness of its concepts. It sets the stage for a comprehensive breakdown of five key theorems in calculus: the fundamental theorem of single-variable calculus, the fundamental theorem of line integrals, Green's theorem, Stokes's theorem, and the Divergence Theorem. The speaker's goal is to illustrate how these theorems are related and to provide a perspective that sees multivariable calculus as a unified whole rather than a collection of disparate parts.
📐 Fundamental Theorem of Single Variable Calculus Explained
This paragraph delves into the fundamental theorem of single-variable calculus, offering an intuitive explanation of integration and differentiation. It breaks down the theorem using Leibniz notation, explaining the concept of derivatives as slopes and integrals as infinite sums of infinitesimally small changes in the function's value. The paragraph emphasizes the importance of understanding these basic concepts to appreciate the interconnectedness of calculus as a whole.
🔍 Exploring Line Integrals and Vector Fields
The focus shifts to line integrals, particularly those of vector fields, which are likened to functions outputting vectors at each point in space. The paragraph explains how line integrals are calculated by taking the dot product of the derivative of a curve and the vector field at various points along the curve. It also introduces the concept of the gradient, a vector field derived from the partial derivatives of a multivariable function, pointing in the direction of greatest change of the function's value.
🌐 Green's Theorem and the Connection to Vector Fields
Green's theorem is introduced as a bridge between line integrals of vector fields and double integrals over an area. The paragraph explains how the theorem relates the line integral around a closed curve to a double integral over the area enclosed by that curve. It discusses the concept of 'curl,' a measure of how much a vector field curves or rotates, and how this is represented in the theorem's formula. The paragraph aims to show the broader implications of line integrals in the context of multivariable calculus.
🌀 Stokes's Theorem and the Generalization of Derivatives
Stokes's theorem is presented as an extension of Green's theorem to three-dimensional spaces, involving surface integrals and the curl of a vector field. The paragraph explains how the theorem equates the surface integral of the curl to the line integral around the boundary of the surface. It touches on the concept of the curl as a vector field that indicates the amount of 'curliness' or rotation in the original vector field.
📏 Divergence Theorem and the Summation of Vector Field Properties
The Divergence Theorem is introduced, focusing on integrals over volumes and the concept of divergence, which measures how a vector field expands or contracts. The paragraph describes how the theorem relates the surface integral of the vector field to the triple integral of the divergence over the enclosed volume. It emphasizes the theorem's role in understanding the flux of a vector field through a closed surface and its significance in the broader framework of calculus.
🔑 The Generalized Stokes's Theorem: Unifying Multivariable Calculus
The paragraph culminates in the presentation of the Generalized Stokes's Theorem, which encapsulates the pattern observed across all the theorems of multivariable calculus. It states that the integral of a differential form's exterior derivative over a shape is equal to the integral of the differential form over the boundary of that shape. The speaker reflects on the unifying nature of this theorem and its implications for understanding calculus in any number of dimensions.
🚀 The Power of Perspective in Mathematical Understanding
In the concluding paragraph, the speaker shares a personal anecdote about gaining a new perspective on multivariable calculus from a friend, illustrating the power of viewing complex concepts from different angles. The paragraph emphasizes the idea that all of calculus can be seen as interconnected and that this realization can be transformative for understanding advanced mathematical concepts.
Mindmap
Keywords
💡Multivariable Calculus
💡Theorems
💡Fundamental Theorem of Single-Variable Calculus
💡Line Integrals
💡Gradient
💡Green's Theorem
💡Stokes's Theorem
💡Divergence Theorem
💡Generalized Stokes' Theorem
💡Perspective
Highlights
The transcript discusses the interconnectedness of multivariable calculus concepts, aiming to provide a unified perspective on the subject.
The speaker shares personal experiences and insights from a roommate named Ari, who emphasized the holistic nature of multivariable calculus.
The fundamental theorem of single variable calculus is introduced, serving as a foundational concept for building up to more complex theorems.
Leibniz notation is explained as a way to understand the geometric intuition behind calculus formulas.
The concept of derivatives as slopes and integrals as infinite sums is simplified for intuitive understanding, with the acknowledgment that this simplification has limitations in higher dimensions.
Line integrals are introduced as integrals over a line, specifically in the context of vector fields, which are likened to functions that output vectors.
The gradient of a multivariable function is described as a vector field that points in the direction of greatest change of the function's value.
The fundamental theorem of line integrals is presented, relating the line integral of a gradient to the difference in function values at curve endpoints.
Green's theorem is introduced, connecting a line integral around a closed curve to a double integral over the enclosed area.
The curl of a vector field is explained as a measure of how much the field curves or rotates around a point.
Stokes's theorem is presented as an extension of Green's theorem to three-dimensional spaces, involving surface integrals and the curl.
The Divergence theorem is introduced, relating a volume integral of a vector field to a surface integral over the boundary of that volume.
The concept of divergence as a scalar function measuring how much a vector field points towards or away from itself is explained.
The Generalized Stokes' Theorem is introduced as a unifying principle for all the theorems discussed, generalizing them into a single formula.
The transcript emphasizes the importance of perspective in understanding complex mathematical concepts, drawing a parallel to the unique viewpoint of astronauts observing Earth.
The speaker concludes by reflecting on the interconnectedness of mathematical theorems and the value of discussing and sharing perspectives with others.
A humorous recommendation is made to find a physics and computer science friend in college for enlightening mathematical discussions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: