Tensors for Beginners 8: Linear Map Transformation Rules
TLDRThis video script explores the transformation rules of linear maps between different bases in a mathematical context. It explains how to determine the components of a vector transformed by a linear map, using matrix multiplication in the 'e' basis. The script delves into deriving a new matrix for a transformed basis, emphasizing the contravariant nature of vector components and the covariant transformation of basis vectors. It simplifies tensor notation using Einstein's summation convention, which omits explicit summation signs for clarity. The video concludes with an introduction to (1,0), (0,1), and (1,1)-tensors, setting the stage for the discussion of the metric tensor in a subsequent video.
Takeaways
- 📚 The video discusses transformation rules for linear maps when transitioning between different bases.
- 🔍 It begins with an example of a linear map represented by a matrix in the 'e' basis, which transforms basis vectors e_1 and e_2 in specific ways.
- 📝 The script explains how to find the components of the vector L(V) by multiplying the column vector representing V by the matrix L, resulting in components [1/2, 2].
- 🔄 The concept of contravariance is introduced, explaining the need for a backward transform when dealing with vector components changing bases.
- 🆕 The necessity to find a new matrix for the transformed basis is highlighted, involving determining L~ coefficients for the output vectors using the new basis vectors.
- 🔢 A step-by-step process is outlined to find the L~ coefficients, involving rewriting new basis vectors in terms of the old, using linearity, and applying definitions and transformations.
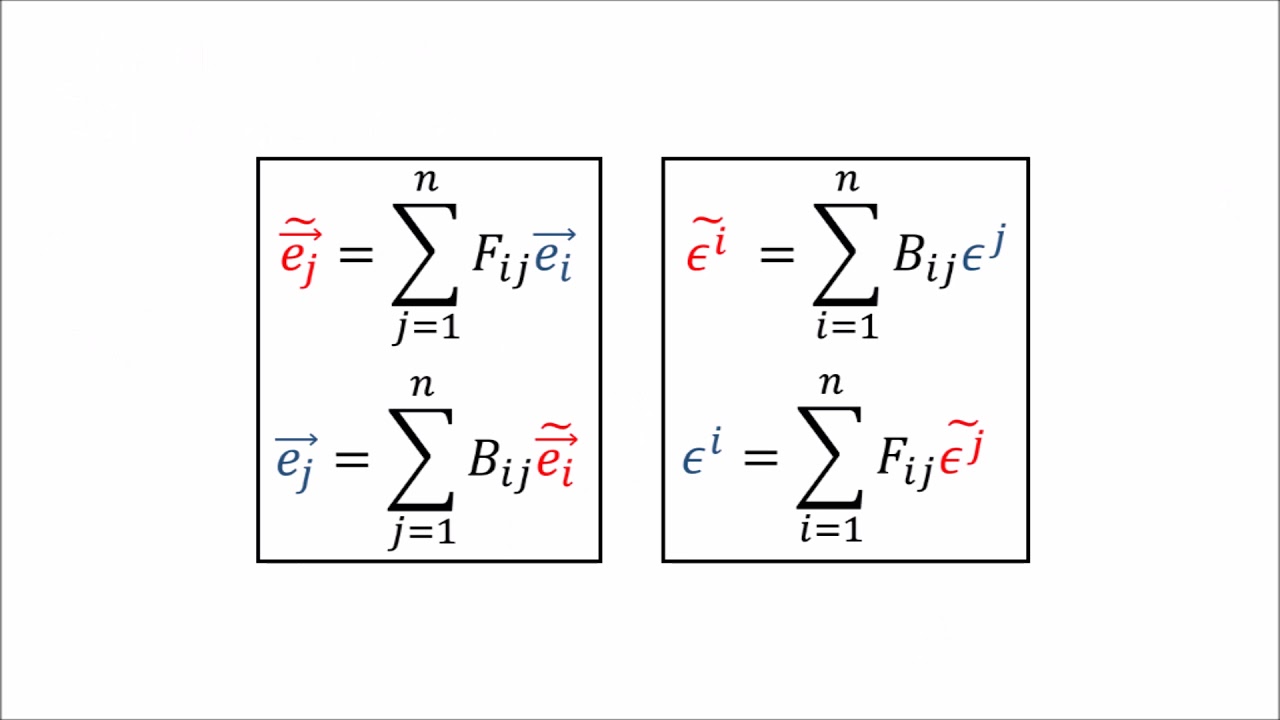
- 🧩 The video simplifies the process by illustrating how to transform matrix coordinates from one basis to another using both forward and backward transformations.
- 📉 It demonstrates the practical application of the new matrix L~ in transforming the basis vector components and verifies the results using the new basis.
- 🎓 The script introduces Einstein's notation as a shorthand for tensor components, simplifying the notation by omitting summation signs when indices are repeated.
- 📚 The video concludes with the classification of different types of tensors: (1,0)-tensors for basis covectors and vector components, (0,1)-tensors for basis vectors and covector components, and (1,1)-tensors for linear maps.
- 🔚 The final takeaway is the预告of the next video, which will cover the metric tensor as the final example of a tensor.
Q & A
What are the transformation rules for linear maps when changing from one basis to another?
-The transformation rules for linear maps involve using both the forward and backward transformations. To find the new matrix representation in a different basis, you multiply the original matrix by the backward transformation matrix on the left and by the forward transformation matrix on the right.
Why does the linear map turn e_1 into 0.5 e_1 and e_2 into 2 e_2?
-The linear map's transformation of the basis vectors e_1 and e_2 is defined by the matrix that represents the linear map in the given 'e' basis. The transformation is a result of the matrix's effect on the basis vectors, scaling them according to the matrix's elements.
What is the significance of the vector V with components [1,1] in the script?
-Vector V with components [1,1] is used as an example to demonstrate how the linear map L transforms a vector when the transformation is represented in the 'e' basis. The transformation results in the new vector components [1/2, 2].
How do you determine the components of the output vector L(V) in the 'e' basis?
-To determine the components of L(V), you multiply the column vector representing V by the matrix representing the linear map L. This multiplication yields the new components of the transformed vector in the 'e' basis.
What is the contravariant transformation of vector components?
-The contravariant transformation of vector components involves applying the backward transformation to the components in the old basis to obtain the components in the new basis. This is because vector components are contravariant, meaning they transform in the opposite way to the basis vectors.
What does the L~ matrix represent in the context of the script?
-The L~ matrix represents the new matrix that describes how to construct output vectors using the new basis vectors (e~). It is derived by applying the transformation rules for linear maps to the original matrix L.
How can you simplify the process of transforming matrix components using Einstein's notation?
-Einstein's notation simplifies the process by omitting summation signs when an index variable appears on both the top and bottom of a term. This implies that a summation over that index is understood to be present, making the notation more concise and easier to work with.
What is the role of the Kronecker delta in transforming matrix components?
-The Kronecker delta acts as a summation index canceller. When multiplying a matrix by the identity matrix, the Kronecker delta allows for the cancellation of summation indices, effectively leaving the original matrix components unchanged.
How does the script define (1,0)-tensors, (0,1)-tensors, and (1,1)-tensors?
-In the script, (1,0)-tensors are basis covectors and vector components that transform using the contravariant law. (0,1)-tensors are basis vectors and covector components that transform using the covariant law. (1,1)-tensors are linear maps that transform using both the forward and backward matrices, making them both contravariant and covariant.
What is the final example of a tensor that the script mentions for the next video?
-The script mentions that the final example of a tensor to be discussed in the next video is the metric tensor.
Outlines
📚 Linear Map Transformation Rules
This paragraph introduces the concept of how linear maps transform when switching between different bases. It uses a matrix representation of a linear map 'L' expressed in the 'e' basis, which turns e_1 into 0.5 e_1 and e_2 into 2 e_2. The process of finding the components of the vector L(V) with components [1,1] is demonstrated by matrix multiplication, resulting in [1/2, 2]. The paragraph also discusses the backward transformation and the need to find new matrix coefficients for the transformed basis vectors, emphasizing the contravariant nature of vector components.
🔍 Deriving New Basis Matrix for Linear Maps
The focus of this paragraph is on deriving the new matrix representation for a linear map in a different basis. It explains the process of using the forward and backward transformations to find the new matrix 'L~' that operates in the new basis. The paragraph illustrates the steps to transform the basis vectors and solve for the 'L~' coefficients. It also simplifies the derivation by dropping summation signs and using Einstein's notation, which assumes summation over repeated indices. The result is a more concise and clear derivation, leading to the final transformation of the matrix components using both forward and backward transformations.
🎯 Simplifying Tensor Transformations with Einstein's Notation
This paragraph discusses the simplification of tensor transformations using Einstein's notation, which omits explicit summation signs for repeated indices. It explains how this notation makes derivations more concise and clear. The paragraph also introduces the concept of Kronecker deltas as summation index cancellers and demonstrates their use in simplifying matrix multiplication with the identity matrix. The paragraph concludes with a quick derivation of the backward transformation for matrix components using the new notation and the properties of Kronecker deltas, showcasing the efficiency of Einstein's notation in tensor calculus.
🧭 Tensor Classification and Transformation Laws
The final paragraph summarizes the key concepts of tensor transformations and introduces the classification of tensors based on their transformation laws. It explains that basis covector components and vector components, which are contravariant, are referred to as (1,0)-tensors. Basis vectors and covector components, which are covariant, are called (0,1)-tensors. Linear maps, which transform using both forward and backward transformations, are classified as (1,1)-tensors. The paragraph also previews the next topic, the metric tensor, which will be the final example of a tensor discussed in the subsequent video.
Mindmap
Keywords
💡Linear Map
💡Basis
💡Matrix
💡Vector Components
💡Backward Transform
💡Contravariant
💡(1,0)-Tensor
💡Forward Transform
💡Einstein's Notation
💡Metric Tensor
Highlights
Exploration of transformation rules for linear maps when transitioning between bases.
Introduction of a linear map represented by a matrix in the 'e' basis.
Explanation of how the linear map transforms basis vectors e_1 and e_2.
Multiplication of a vector's column vector by the matrix to find the transformed vector's components.
Discussion on the contravariant nature of vector components and the use of the backward transform.
The need to find a new matrix for the e~ basis vectors to determine output vector components.
Derivation of the new matrix coefficients L~ using the forward and backward transformations.
Use of linearity of L to simplify the expression for the transformed basis vectors.
Rearrangement of sums and rewriting of basis vectors to solve for L~ coefficients.
Transformation of matrix coordinates from old to new basis by multiplying with backward and forward transforms.
Practical demonstration of transforming a matrix L~ in the new basis using multiplication.
Verification of the new L~ matrix by transforming new basis vector components.
Introduction of Einstein's notation for simplifying tensor component expressions.
Derivation of the backward transformation for matrix components using Einstein's notation.
Explanation of Kronecker delta as a summation index canceller in tensor expressions.
Categorization of tensors based on their transformation properties: (1,0), (0,1), and (1,1)-tensors.
Upcoming introduction of the metric tensor as the final example of a tensor in the next video.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: