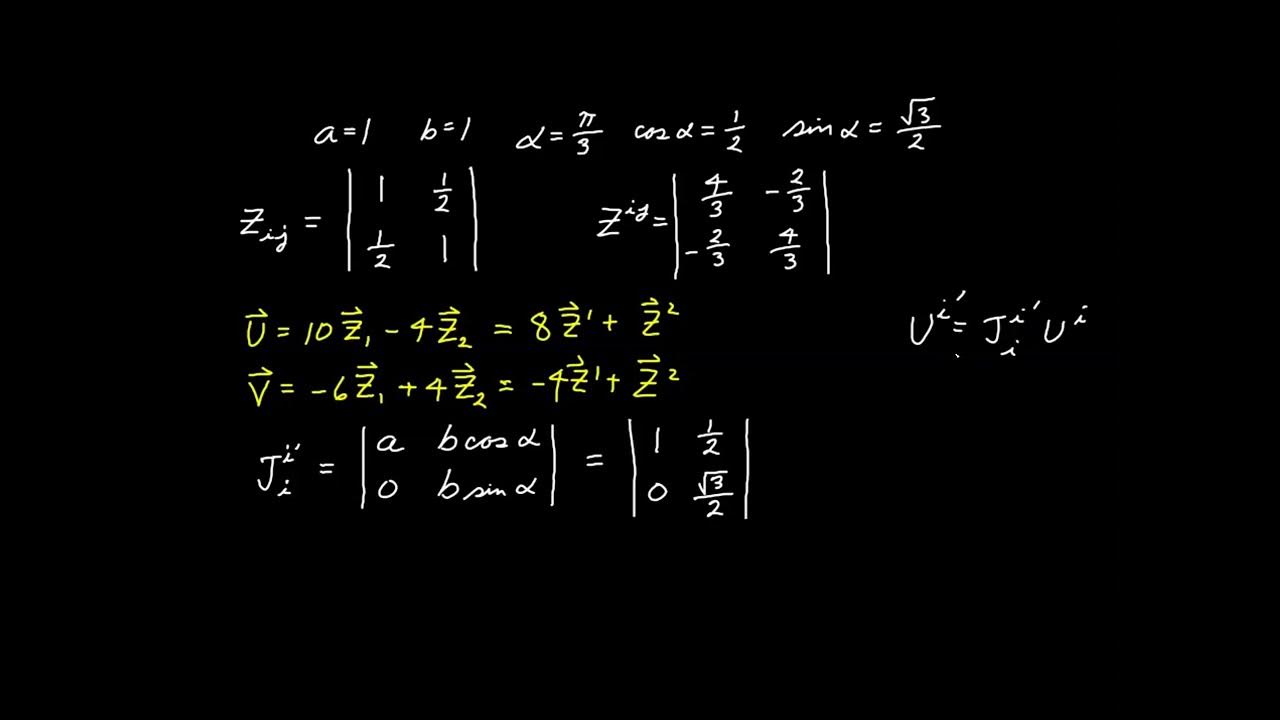Tensor Calculus For Physics Majors 002 | Vector Transformations and Vectors as Matrices

Andrew Dotson

26 May 201839:38

EducationalLearning

32 Likes 10 Comments

TLDRThis video concludes a series on tensor calculus with a focus on vector transformations and their matrix representations. It explains how to convert between Cartesian coordinates using rotation around the z-axis, deriving the transformation equations for x', y', and z'. The script delves into the invariance of the space-time interval under orthogonal transformations and explores the concept of expressing vectors through their transformation rules, akin to tensor definitions. It also introduces Dirac notation for vectors, demonstrating how to perform operations like dot and outer products, and concludes with transforming between different bases using this notation.

Takeaways

📚 The video concludes the preliminary vector topics for a series on tensor calculus, focusing on vector transformations and representing vectors as matrices.
🔄 The script explains the process of converting Cartesian coordinates \( (x, y) \) into rotated coordinates \( (x', y') \) by rotating the axes about the z-axis, using the equations \( x' = x \cos(\theta) + y \sin(\theta) \) and \( y' = -x \sin(\theta) + y \cos(\theta) \).
📏 It demonstrates the derivation of the rotation transformation equations and emphasizes the importance of understanding the derivation process for a deeper comprehension of the subject.
🧭 The video connects the derived rotation transformation to the concept of tensors, which are quantities that transform according to specific rules, maintaining the invariance of physical properties.
📉 The script shows that the space-time interval is invariant under the described orthogonal transformations, which is a crucial concept in physics.
🔢 The video derives expressions for velocity and acceleration in the rotated reference frame by taking derivatives of the position transformation equations.
📈 The transformation of vectors into matrices is introduced, with vectors being represented in Dirac notation as column matrices and their transformations expressed in terms of matrix equations.
🤖 The concept of Dirac notation is explained, including how to represent vectors as ket vectors and calculate dot products and outer products using matrix operations.
📊 The script covers how to express unit vectors in terms of column vectors and calculate the inner product between them, highlighting the orthonormality of basis vectors.
🔗 The completeness relation for unit vectors is discussed, showing how any vector can be expressed as a linear combination of basis vectors using the identity matrix.
🔄 The process of transforming between different bases using Dirac notation is explained, including how to find the components of a vector in a new basis by taking inner products with the new basis vectors.

Q & A

What is the main topic of the video?
-The main topic of the video is vector transformations and representing vectors as matrices in the context of tensor calculus.
Why is it necessary to convert x and y into x' and y'?
-It is necessary to convert x and y into x' and y' to express equivalent answers from different coordinate systems, specifically after rotating the axes about the z-axis.
What is the transformation formula for X' and Y' when rotating about the z-axis?
-The transformation formula is X' = X * cos(theta) + Y * sin(theta) and Y' = -X * sin(theta) + Y * cos(theta), with Z' remaining equal to Z.
What is the significance of deriving the transformation equations in the video?
-Deriving the transformation equations is significant to understand how vectors transform under rotations and to establish a foundation for further topics in tensor calculus.
How does the video demonstrate the invariance of the space-time interval under transformation?
-The video shows that the space-time interval, represented as Δs'^2 = Δs^2, remains invariant under the transformation by taking derivatives of the transformation equations and showing that the sum of the squares of the transformed components equals the sum of the squares of the original components.
What is the relationship between the transformation of vectors and tensors?
-The transformation of vectors is analogous to how tensors are defined, as both obey certain transformation rules under coordinate changes, which is a key concept in understanding the properties of tensors.
What is Dirac notation and how is it used in the video?
-Dirac notation is a formalism used in quantum mechanics to represent quantum states as vectors. In the video, it is used to represent vectors as column matrices and to perform operations such as dot products and outer products.
How are unit vectors represented in Dirac notation?
-Unit vectors are represented as column vectors in Dirac notation, with each unit vector corresponding to a basis in the coordinate system, such as i_hat, j_hat, and k_hat for Cartesian coordinates.
What is the purpose of the completeness relation in the context of the video?
-The completeness relation, which states that the identity matrix is the sum of the outer products of an orthonormal basis set, is used to express any vector as a linear combination of its basis vectors, scaled by their components.
How does the video explain the transformation to a new basis using Dirac notation?
-The video explains that transforming to a new basis involves taking the inner product of the new basis vector with the original vector, which gives the component of the original vector in the new basis.
What is the next topic the video series will cover after the preliminary vector review?
-The next topic the video series will cover is two-index tensors.

Outlines

00:00

📚 Introduction to Vector Transformations and Matrices

This paragraph introduces the topic of vector transformations and the representation of vectors as matrices in the context of tensor calculus. The speaker aims to show the equivalence of physics problems solved in Cartesian coordinates and rotated coordinates, focusing on the rotation about the z-axis. Key formulas for converting x and y into x' and y' are presented, highlighting the importance of understanding the underlying physics despite different mathematical expressions.

05:05

🔍 Deriving Transformation Equations and Invariance

The speaker delves into the derivation of transformation equations from polar to Cartesian coordinates, emphasizing the trigonometric identities involved. The paragraph explores the invariance of the space-time interval under orthogonal transformations, which is a significant concept in physics. The process involves taking derivatives of the transformation equations and demonstrating that the interval remains unchanged, indicating the relativity of transformations.

10:07

📐 Vectors and Tensors Transformation Rules

This section discusses the transformation rules for vectors and tensors, starting with the transformation of displacement vectors into velocity and acceleration. The speaker explains how to find the derivatives of the transformation equations and introduces the concept of expressing vectors in a manner similar to tensors. The paragraph concludes with the mathematical formulation of these transformations, laying the groundwork for understanding tensor behavior under coordinate changes.

15:14

🧬 Dirac Notation and Vector Representation

The introduction of Dirac notation for vectors is the focus of this paragraph. The speaker explains how vectors can be represented as column matrices and how this notation simplifies calculations. The paragraph covers the representation of dot products and the transformation of vectors using this notation, including the handling of complex components and the concept of outer products.

20:14

📚 Unit Vectors and Completeness Relation

The speaker discusses the representation of unit vectors in Cartesian coordinates using column vectors and explores the concept of the completeness relation. This involves the summation of outer products of orthonormal basis vectors equating to the identity matrix. The paragraph also explains how to calculate the inner product between unit vectors and the significance of this in the context of orthonormal basis vectors.

25:18

🔗 Matrix Elements and Transformation to a New Basis

This paragraph focuses on how to extract specific elements from a matrix formed by the outer product of two vectors. The speaker demonstrates the process of finding matrix elements using Dirac notation and introduces the concept of transforming vectors into a new basis. The paragraph concludes with the mathematical expression for this transformation and its equivalence to the traditional method.

30:20

🚀 Conclusion and Transition to Two-Index Tensors

The final paragraph wraps up the preliminary vector review and sets the stage for the next topic: two-index tensors. The speaker reflects on the importance of understanding vector transformations in the context of tensor definitions and invites feedback from the audience. The paragraph concludes with an anticipation of delving into the specifics of two-index tensors in the subsequent video.

Mindmap

Keywords

💡Vector Transformations

Vector transformations refer to the process of converting vector components from one coordinate system to another. In the video, this concept is central to understanding how vectors behave under rotations, specifically around the z-axis. The script discusses converting Cartesian coordinates (X, Y) into a new set of coordinates (X', Y') through rotation, which is essential for the theme of tensor calculus.

💡Tensor Calculus

Tensor calculus is a mathematical framework used to handle multi-dimensional arrays, known as tensors, and their transformations. The video is part of a series on this topic, aiming to explain how tensors can be represented and manipulated, especially in the context of vector transformations and rotations.

💡Cartesian Coordinates

Cartesian coordinates are a system of defining positions using perpendicular axes, typically labeled X, Y, and Z. The script uses Cartesian coordinates as a starting point for the problem-solving process, where it initially keeps the problem in these coordinates before rotating to a new coordinate system.

💡Polar Coordinates

Polar coordinates represent points in a plane using the distance from a reference point (origin) and the angle from a reference direction (usually the positive X-axis). The video script mentions polar coordinates in the context of deriving the rotation formulas for converting Cartesian coordinates to rotated coordinates.

💡Trigonometric Identities

Trigonometric identities are equations that hold true for the sine and cosine functions, such as the sum and difference formulas. In the script, these identities are used to derive the expressions for X' and Y' in terms of X, Y, and the rotation angle theta.

💡Orthogonal Transformation

An orthogonal transformation is a linear transformation that preserves the dot product, and hence, the length of vectors. The video script explains that the space-time interval is invariant under such transformations, which is a key property in the study of tensor calculus.

💡Space-Time Interval

The space-time interval is a concept from the theory of relativity that remains constant in all inertial frames of reference. In the script, the invariance of this interval under orthogonal transformations is demonstrated, which is a fundamental aspect of the video's discussion on tensor calculus.

💡Dot Product

The dot product, also known as the scalar product, is an operation that takes two vectors and returns a single number, representing the product of the magnitudes of the two vectors and the cosine of the angle between them. The script discusses the dot product in the context of transforming vectors and calculating the inner product between vectors represented as column vectors.

💡Dirac Notation

Dirac notation, introduced by physicist Paul Dirac, is a formalism used in quantum mechanics to represent quantum states as vectors. The video script uses this notation to represent vectors as column matrices and to perform operations such as the dot product and outer product.

💡Outer Product

The outer product of two vectors results in a matrix whose elements are the products of the elements of the original vectors. In the script, the outer product is used to construct a square matrix from the components of two vectors, which is then related to the concept of the identity matrix in the context of basis transformations.

💡Unit Vectors

Unit vectors are vectors of length one, used to specify direction in a particular coordinate system. The script discusses unit vectors in the context of Cartesian coordinates (i-hat, j-hat, k-hat) and uses them to express the completeness relation and to transform between different bases.

💡Completeness Relation

The completeness relation is a statement that the sum of the outer products of an orthonormal basis set of vectors equals the identity matrix. In the script, this relation is used to express any vector in terms of its components along the basis vectors and to transform between different bases using Dirac notation.

Highlights

Introduction to vector transformations and representing vectors as matrices in the context of tensor calculus.

Explaining the equivalence of physics problems solved in Cartesian coordinates and rotated coordinates.

Derivation of the rotation transformation formula for converting x and y into x' and y' by rotating the axis about the z-axis.

Use of polar coordinates to derive the rotation transformation equations.

Explanation of trigonometric identities in the context of deriving vector transformations.

Substitution of x and y with R cos(alpha) and R sin(alpha) to simplify the transformation equations.

Discussion on the invariance of the space-time interval under orthogonal transformations.

Demonstration that the interval between two points remains invariant under rotation.

Introduction to expressing vectors in a manner similar to tensors through transformation rules.

Derivation of the relationship between velocity and displacement vector components under rotation.

Exploration of the transformation of vectors into different reference frames using Dirac notation.

Explanation of how to represent vectors as column matrices and the significance of Dirac's notation.

Calculation of dot products between vectors represented as column and row matrices.

Introduction to the outer product of two vectors and its resulting square matrix form.

Expression of unit vectors in Cartesian coordinates using column vectors and their properties.

Use of the completeness relation to express any vector in terms of its components in an orthonormal basis.

Method to determine specific elements of a matrix formed by the outer product of two vectors.

Transformation of vectors into a new basis using Dirac notation and the concept of lambda transformation.

Conclusion summarizing the preliminary vector review and its connection to tensor definitions.

Transcripts

Browse More Related Video

Tensors for Beginners 8: Linear Map Transformation Rules

Video 26 - Vector Operation Examples

Tensor Calculus Lecture 12b: Inner Products in Tensor Notation

Basic Linear Algebra Concepts for Tensors

Video 11 - Vector Transformations

Are Square Matrices Always Tensors?: A Counter Example

Related Tags

Vector Transformation Tensor Calculus Physics Problem Cartesian Coordinates Rotation Matrix Polar Coordinates Trigonometric Identities Space-Time Interval Dirac Notation Quantum Mechanics