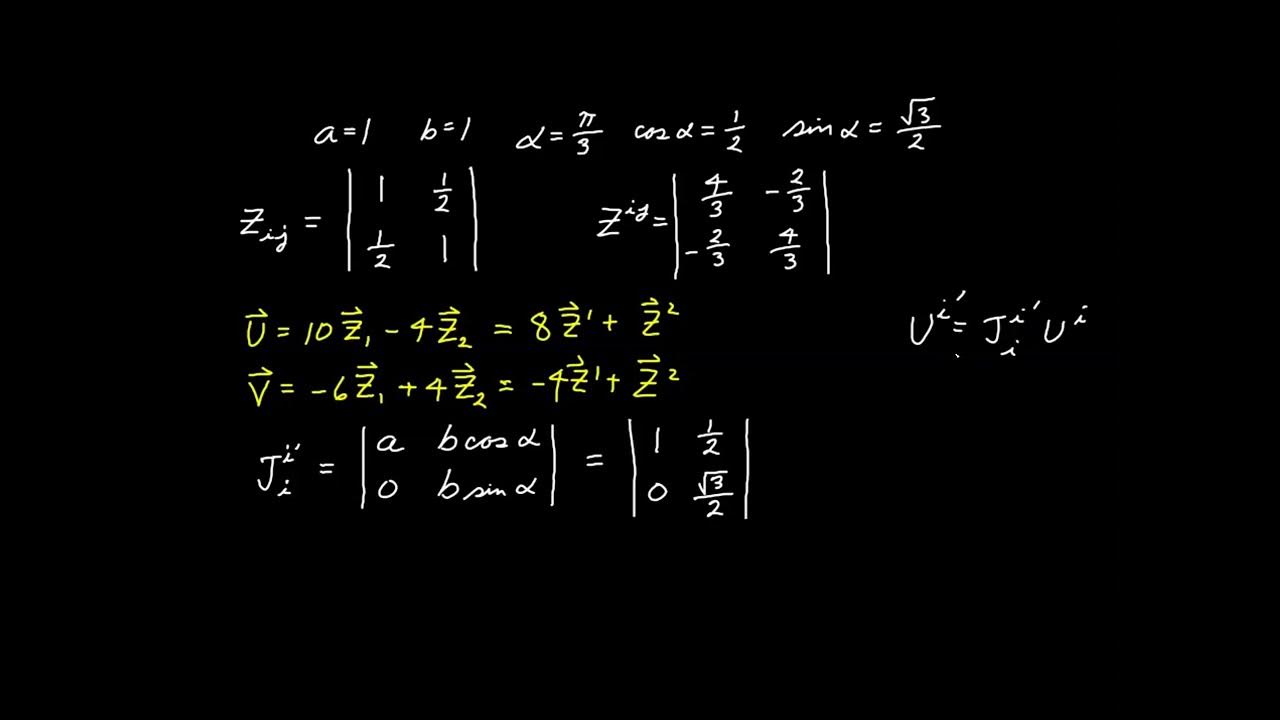Tensor Calculus For Physics Majors #1| Preliminary Vector Stuff part 1

Andrew Dotson

19 May 201853:10

EducationalLearning

32 Likes 10 Comments

TLDRThis lecture series on tensor calculus for physics begins by focusing on scalars and vectors, aiming to build familiarity before delving into tensors. The instructor emphasizes the importance of understanding how quantities transform under different coordinate systems, introducing concepts such as coordinate transformations, invariance, and the properties of vectors. The video also covers the directional derivative, gradient, divergence, and curl, using clear examples and explanations to lay the groundwork for more advanced topics like two-index tensors.

Takeaways

📚 The lecture series is on tensor calculus for physics, closely following the book by Dwight Nu and Shawanda.
🔑 The initial focus is on scalars and vectors before delving into tensors, to build familiarity with their transformation properties.
🧭 Tensors are defined by their transformation laws, which is analogous to defining currency in terms of another, highlighting the importance of understanding change.
📈 Vectors can be defined by their transformation properties, not just magnitude and direction, setting the stage for understanding tensors.
📐 The video introduces the concept of coordinate systems and transformations, essential for understanding how physical quantities change under different frames of reference.
🔍 Scalars are quantities that remain invariant under coordinate transformations, maintaining the same value across different systems.
📉 Vectors are defined by their components in a coordinate system and must obey transformation laws to transition between systems.
🤔 The video emphasizes the importance of understanding the transformation of quantities rather than just their magnitude and direction.
📈📉 The lecturer assumes prior knowledge of basic vector operations such as dot and cross products, and their geometric interpretations.
🔄 The concept of taking derivatives of vectors with respect to scalars, such as time, is introduced, relating to concepts like velocity.
🔍📚 The gradient, divergence, and curl are discussed as vector operations derived from scalar functions, with the gradient giving the direction of maximum change.

Q & A

What is the main topic of the lecture series?
-The main topic of the lecture series is tensor calculus for physics.
Why does the lecturer decide not to start with tensors immediately?
-The lecturer decides not to start with tensors immediately because most people are not comfortable defining objects based on how they change, which is how tensors are usually defined.
What concepts will be the focus of the first and second videos?
-The focus of the first and second videos will be on scalars and vectors, their basic properties, and expressing them in terms of how they transform.
What is a scalar in the context of coordinate transformations?
-A scalar is a quantity that remains unchanged under a coordinate transformation, meaning if a quantity lambda is a scalar, then lambda equals lambda prime after the transformation.
How can vectors be defined in terms of transformation?
-Vectors can be defined in terms of transformation by breaking them into components that contain the information of the vector and obey certain transformation laws to go from one coordinate system to another.
What assumptions is the lecturer making about the audience's prior knowledge?
-The lecturer assumes that the audience has some prior knowledge, such as understanding dot and cross products of vectors, and the concept of taking derivatives of vectors with respect to scalars like time.
What is the concept of a gradient in the context of scalar functions?
-The concept of a gradient is taking the derivative of a scalar function with respect to displacement, which gives the direction in which the function changes the most.
What are the properties of the unit vectors I, J, and K in a 3D coordinate system?
-The unit vectors I, J, and K are orthonormal, meaning they are perpendicular to each other and all have unit length. They form a complete set of basis vectors that can be used to express any vector in the space.
What is the significance of the Kronecker Delta in the context of dot products of basis vectors?
-The Kronecker Delta is a shorthand that captures the relationship of dot products between basis vectors, where it equals 1 if the indices are the same and 0 if they are different.
How is the cross product of two vectors represented using the Levi-Civita symbol?
-The cross product of two vectors can be represented using the Levi-Civita symbol as a sum over the product of the symbol and the components of the vectors, which simplifies the expression for specific components of the cross product.
What physics problem is solved in the script using two different coordinate systems?
-The physics problem solved in the script is that of a block on an inclined plane, where the forces acting on the block are analyzed using both the original XY coordinate system and a rotated coordinate system aligned with the plane.

Outlines

00:00

📚 Introduction to Tensor Calculus for Physics

The lecture series begins with an introduction to tensor calculus, a mathematical framework essential for advanced physics. The speaker emphasizes that tensors are defined by their transformation properties rather than their intrinsic values, akin to defining currency in terms of another. The initial focus is on scalars and vectors, familiar concepts to most, to build an understanding before delving into tensors. The goal is to express these familiar concepts in terms of their transformation behavior, setting the stage for a deeper exploration of tensor properties in subsequent videos.

05:00

📐 Coordinate Systems and Transformations

This paragraph delves into the concept of coordinate systems and their transformations, highlighting the importance of scalars and vectors in describing physical phenomena. Scalars are introduced as quantities that remain invariant under coordinate transformations, while vectors are characterized by their transformation laws. The speaker also touches on the idea of a tensor implicitly providing a theory of relativity due to its transformation properties. The paragraph establishes the groundwork for understanding how physical laws remain consistent across different coordinate systems.

10:01

🔍 Exploring Vector Operations and Properties

The script discusses fundamental vector operations such as the dot product, which measures the degree of similarity in direction between two vectors, and the cross product, which yields a vector perpendicular to the plane containing the two original vectors. The properties of unit vectors and the concept of orthonormal basis are introduced, leading to the idea that any vector can be expressed as a linear combination of these basis vectors. The paragraph also covers the gradient, divergence, and curl, which are vector operations applied to scalar fields, and their physical interpretations.

15:04

📝 Notation and Orthonormal Basis Vectors

The speaker introduces a new notation for unit vectors and explains the concept of an orthonormal basis set, which allows any vector to be constructed as a linear combination of basis vectors. The Kronecker Delta is introduced as a shorthand for expressing the properties of these basis vectors, particularly their orthogonality and unit length. The paragraph emphasizes the importance of understanding different notations and their implications in vector mathematics.

20:06

📚 Dot and Cross Products in Component Form

This section explores the calculation of dot and cross products in terms of vector components. The dot product is expressed as a sum over the products of corresponding components, while the cross product is detailed through its components in the context of the Levi-Civita symbol. The speaker illustrates how to calculate the components of the cross product abstractly, providing a deeper understanding of vector operations.

25:09

📐 Vector Components in Different Coordinate Systems

The script discusses how to represent vector components in different coordinate systems, starting with the Cartesian coordinate system and moving on to a rotated coordinate system aligned with an inclined plane. The process of decomposing forces acting on a block into their respective components in the new coordinate system is explained, emphasizing the importance of understanding vector decomposition in various contexts.

30:11

🔧 Solving the Block on an Inclined Plane Problem

The paragraph presents a physics problem involving a block on an inclined plane, aiming to find the total force acting on the block considering gravity, normal force, and friction. The problem is approached by breaking down the forces into their x and y components and solving for the acceleration of the block in both the original and a rotated coordinate system. The solution demonstrates the equivalence of physical descriptions across different coordinate systems.

35:16

🔄 Coordinate Transformation and Equivalence

The final paragraph wraps up the discussion by emphasizing the importance of coordinate transformation. It highlights that different coordinate systems can describe the same physical scenario, and thus there must be a way to map one system to another. The speaker sets the stage for the next video, which will delve into the specifics of these transformations, ensuring that the audience understands the fundamental principles before moving on to more complex topics.

Mindmap

Keywords

💡Tensor Calculus

Tensor calculus is a branch of mathematics that deals with the manipulation of tensors, which are generalizations of scalars, vectors, and other geometric objects. In the video, the theme revolves around introducing tensor calculus to physics, starting with foundational concepts like scalars and vectors before delving into more complex tensor operations. The script mentions that the lecture series will follow 'Tensor Calculus for Physics' by Dwight努 and Shawanda, indicating the educational nature of the content.

💡Scalars

Scalars are mathematical objects that have only magnitude and no direction. They are contrasted with vectors in the script, which have both magnitude and direction. The video aims to build up from scalars to more complex concepts, using the example of scalars to illustrate how quantities can be invariant under coordinate transformations, which is fundamental to understanding tensors.

💡Vectors

Vectors are quantities that possess both magnitude and direction. In the script, vectors are introduced as familiar concepts to the audience before transitioning to tensor transformations. The lecturer discusses how vectors can be defined not only by their magnitude and direction but also by how they transform under different coordinate systems, which is essential for understanding tensor behavior.

💡Coordinate Systems

Coordinate systems are used to describe the position of points in a geometric space. The script explains how different people might describe the same location using different coordinate systems, highlighting the concept of coordinate transformation. This is crucial for understanding how physical quantities, such as tensors, change under different reference frames.

💡Transformation

Transformation in the context of the video refers to how mathematical objects like tensors, vectors, and scalars change when the coordinate system is altered. The script emphasizes the importance of understanding transformations to define tensors and to connect the concept of how vectors transform to the more abstract notion of tensor transformations.

💡Dot Product

The dot product is an algebraic operation that takes two vectors and returns a scalar. In the script, it is explained as the product of the magnitudes of two vectors and the cosine of the angle between them. The dot product is used to illustrate the relationship between vectors and to introduce the concept of orthogonality, where the dot product is zero.

💡Cross Product

The cross product is an operation between two vectors in three-dimensional space, resulting in a vector that is perpendicular to the plane containing the two original vectors. The script describes the cross product in terms of its magnitude and the angle between the vectors, and it introduces the concept of anti-symmetry, where the cross product of two vectors is the negative of the cross product in reverse order.

💡Gradient

The gradient is a vector operator that represents the direction and rate of the fastest increase of a scalar function. In the script, the gradient is introduced as a way to find the direction in which a scalar function, such as temperature or pressure, changes the most. This concept is foundational for understanding how scalar fields can be related to vector quantities.

💡Divergence

Divergence is a measure of how a vector field is spreading out or converging at a point. In the script, it is described as a scalar quantity obtained by taking the dot product of the gradient operator with a vector, and it is likened to water flowing through a sink, indicating a flow rate of something spreading out from a point.

💡Curl

Curl is a vector quantity that represents the rotation or 'circulation' of a vector field around a point. The script describes the curl as being similar to a whirlpool effect, indicating the rotational aspect of a vector field. It is used to illustrate the behavior of vector fields in terms of rotation.

💡Unit Vectors

Unit vectors are vectors with a magnitude of one, typically used to establish direction in coordinate systems. In the script, unit vectors are introduced as the basis for defining other vectors in space, with properties that they are perpendicular to each other and have unit length, making them orthonormal.

💡Basis Vectors

Basis vectors are a set of linearly independent vectors that span a space. In the script, the concept of basis vectors is introduced to explain how any vector can be expressed as a linear combination of these basis vectors. The unit vectors I, J, and K are given as examples of a complete set of orthonormal basis vectors in three-dimensional space.

💡Metric Tensor

The metric tensor is a mathematical object that provides a way to measure distances and angles in a given space, taking into account the curvature of that space. In the script, the components of the metric tensor are introduced when discussing the dot product of basis vectors that are not unit vectors, indicating how the space's geometry can affect measurements.

💡Levi-Civita Symbol

The Levi-Civita symbol, also known as the permutation symbol, is used in the script to represent the components of the cross product in a more abstract and concise way. It is defined by its properties related to cyclic and anti-cyclic permutations of indices, and it is used to simplify the expression for specific components of the cross product.

💡Free Body Diagram

A free body diagram is a graphical representation of all the forces acting on an object. In the script, a free body diagram is used to analyze the forces on a block on an inclined plane, including gravity, normal force, and friction, to solve for the components of the forces in different coordinate systems.

Highlights

Introduction to a lecture series on tensor calculus for physics, focusing on foundational concepts before delving into tensors.

Explanation of why tensors are not immediately introduced, due to the unfamiliarity most people have with defining objects by their transformation.

The goal of building up from scalars and vectors to motivate the understanding of tensors through familiar concepts.

Differentiation between defining a vector by its magnitude and direction versus its transformation properties.

Introduction of coordinate systems and the concept of coordinate transformation.

The physics agnosticism regarding coordinate systems, emphasizing the importance of invariant quantities.

Definition of a scalar as a quantity invariant under coordinate transformations.

Vector transformation laws and how they differ from their magnitude and direction definitions.

Assumptions made in the lecture, including prior knowledge of basic vector operations.

Explanation of dot and cross products in the context of vectors and their geometric interpretations.

The concept of derivatives of vectors with respect to scalars, illustrated with the example of velocity as the derivative of position.

Introduction of the gradient, directional derivative, divergence, and curl in the context of scalar and vector fields.

The use of unit vectors and the definition of an orthonormal basis in three-dimensional space.

Elucidation of the Kronecker Delta as a shorthand for the properties of orthonormal basis vectors.

Discussion on the linear independence and spanning of space by basis vectors, essential for understanding vector representation.

Transition to the use of non-unit basis vectors and the implications for dot product calculations.

Introduction of the metric tensor through the components of dot products between basis vectors.

Illustration of the cross product using determinants and the Levi-Civita symbol for component representation.

Application of the concepts to a physics problem involving a block on an inclined plane, showcasing the utility of the discussed mathematical tools.

Solving the block on an inclined plane problem using both traditional and rotated coordinate systems to demonstrate the coordinate independence of physical laws.

Final remarks on the importance of understanding tensor calculus for describing physical phenomena across different coordinate systems.

Transcripts

Browse More Related Video

Contravariant and Covariant Vectors | 1/2

Introduction to Tensors: Transformation Rules

Video 11 - Vector Transformations

Tensors for Beginners 0: Tensor Definition

Tensor Calculus 5b: Invariants Are Tensors

Video 26 - Vector Operation Examples

Related Tags

Tensor Calculus Physics Lecture Series Scalars Vectors Coordinate Systems Transformation Laws Educational Content Mathematical Concepts Physics Tutorial