Are Square Matrices Always Tensors?: A Counter Example
TLDRThis educational video script explores the concept of tensors and their relationship with matrices. It clarifies the misconception that all square matrices are tensors by demonstrating through an example involving a 2x2 matrix derived from Cartesian components of a position vector. The script delves into the transformation of tensor components under orthogonal transformations, specifically rotations, to determine if the matrix qualifies as a Cartesian tensor. The presenter challenges viewers to consider other types of transformations that might allow the matrix to behave as a tensor, prompting engagement and deeper understanding.
Takeaways
- 🧠 The concept of tensors and matrices is explored, emphasizing that not all matrices are tensors, and this is a common misconception among students.
- 📚 Tensors are introduced to physics students as matrices, but this can be misleading as they are not equivalent.
- 📏 The script discusses the conditions under which a matrix can be considered a tensor, specifically focusing on transformations under an orthogonal group.
- 📐 A two-dimensional position vector is used as an example to determine if its matrix representation is a tensor by checking its transformation under rotations.
- 🔍 The importance of agreeing upon a group of transformations for an object to be considered a tensor is highlighted, with the example of the inertia tensor transforming under orthogonal transformations.
- 📊 The script explains the transformation of tensor components under rotations, using the partial derivatives of the new coordinates with respect to the old ones.
- 📘 The transformation coefficients are calculated for the given matrix, which are necessary to determine if the matrix transforms as a tensor under the specified conditions.
- 🔄 The script demonstrates the process of applying a rotation to the matrix and comparing the transformed components to the expected tensor transformation.
- ❌ The example concludes that the given matrix does not transform as a tensor under the tested orthogonal transformation, specifically rotation.
- 🤔 The video poses a question to the audience about the possibility of the matrix transforming as a tensor under more general transformations with arbitrary constants.
- 📝 The script encourages viewers to think critically about the conditions under which a matrix could be considered a tensor and invites discussion in the comment section.
Q & A
What is the relationship between squares and rectangles in terms of tensor representation?
-The script compares the mathematical concept of squares and rectangles to that of tensors and matrices, stating that just as all squares are rectangles but not all rectangles are squares, two indexed tensors can be represented by a square matrix, but not all square matrices are tensors.
What is a tensor in the context of physics?
-In the context of physics, a tensor is a mathematical object that describes a quantity or relationship that is invariant under changes in the coordinate system, such as rotations or translations.
What is the significance of the transformation group in determining if an object is a tensor?
-The transformation group is crucial in determining if an object is a tensor because the object must transform under a specific set of transformations, such as orthogonal transformations, to be considered a tensor.
What are Cartesian tensors?
-Cartesian tensors are tensors that transform under orthogonal transformations and are represented in an orthonormal basis, which is often the case with tensors in flat space and Cartesian coordinates.
What is the process to determine if a matrix is a Cartesian tensor?
-To determine if a matrix is a Cartesian tensor, one must check if it transforms correctly under orthogonal transformations, such as rotations. This involves calculating the transformation coefficients and comparing the transformed components to the original matrix elements.
What are the transformation coefficients used in the script for tensor transformation?
-The transformation coefficients used in the script are the partial derivatives with doubly contravariant indices, which are used to transform the components of a tensor under orthogonal transformations.
How do Cartesian components of vectors transform under rotations?
-Under rotations, the Cartesian components of vectors transform according to the rotation matrix, where the new components are expressed as linear combinations of the original components using cosine and sine of the rotation angle.
What is the result of the script's example calculation for the transformation of a matrix element under rotation?
-The script's example calculation shows that the matrix element does not transform as a tensor under rotation because the left-hand side of the equation (the transformed matrix element) does not equal the right-hand side (the expected result if it were a tensor).
What is the implication of the matrix not transforming as a tensor under the given transformation?
-The implication is that the matrix does not satisfy the conditions to be considered a tensor under the specific transformation (rotation in this case), and thus it cannot be used to represent quantities that are invariant under such transformations.
What is the challenge posed by the script to the viewers?
-The script challenges viewers to consider if there is a type of transformation under which the matrix could transform as a tensor, given a more general set of transformation coefficients instead of the specific sines and cosines used for rotation.
Outlines
🔲 The Relationship Between Tensors and Matrices
The speaker introduces the concept that while all squares are rectangles, not all rectangles are squares, drawing an analogy to tensors and matrices. They discuss the complexity of understanding tensors, especially when introduced to students as matrices, and set the stage to explore whether a specific 2x2 matrix, constructed from Cartesian components of a 2D position vector, behaves as a tensor under orthogonal transformations in an orthonormal basis.
🔄 Transforming Matrix Components and Testing Tensor Behavior
The speaker delves into the transformation of matrix components under rotations to determine if the matrix behaves as a tensor. By calculating transformation coefficients and substituting them into the transformation equations, the speaker demonstrates the step-by-step process of checking if the 1-1 component of the matrix in the primed frame corresponds to the tensor transformation in the unprimed frame. They emphasize the abstract nature of these calculations and proceed to simplify the terms to check for consistency between the primed and unprimed frames.
❌ Conclusion: Matrix Components Do Not Transform as Tensors
The final part reveals that the matrix does not transform as a tensor. The speaker explains that despite following the process for tensor transformation, the left-hand side of the equation does not equal the right-hand side, indicating that the matrix’s components do not transform as tensors under the given rotation. They invite the audience to consider if more general transformations, using arbitrary constants instead of sines and cosines, might yield a tensor transformation, encouraging further thought and discussion.
Mindmap
Keywords
💡Tensor
💡Square Matrix
💡Cartesian Tensor
💡Orthogonal Transformations
💡Transformation Coefficients
💡Contravariant and Covariant Indices
💡Rotation
💡Matrix Element
💡Orthonormal Basis
💡Transformation
💡Summation
Highlights
The concept that all squares are rectangles but not all rectangles are squares is analogous to the idea that two-indexed tensors can be represented by square matrices, but not all square matrices are tensors.
Tensors are often introduced to physics students as matrices, but this video explores the conditions under which a matrix can be considered a tensor.
The video discusses the importance of agreeing upon a group of transformations that an object must transform under to be considered a tensor.
Inertia tensors transform as tensors under orthogonal transformations, and objects represented in an orthonormal basis are called Cartesian tensors.
The video uses a two-by-two matrix constructed from Cartesian components of a two-dimensional position vector to test if it is a tensor.
The transformation of tensor components is explained, specifically how they should transform under orthogonal transformations.
The video demonstrates the process of calculating transformation coefficients for the matrix elements under rotations.
The Cartesian components of vectors transform under rotations, and the video shows the mathematical expressions for these transformations.
The video calculates the transformation coefficients by taking derivatives of the prime coordinate with respect to the unprimed coordinate.
The video shows the process of determining if the matrix components transform as tensors by summing over the indices L and M.
The video concludes that the matrix does not transform as a tensor under the tested conditions, specifically rotations.
The video challenges viewers to consider if there are more general transformations under which the matrix could transform as a tensor.
The concept of tensors and their transformation is related to the broader topic of linear algebra and its applications in physics.
The video uses a step-by-step approach to demonstrate the mathematical process of determining tensor transformation.
The video provides a practical example of how to apply the theory of tensor transformation to a specific matrix.
The video encourages viewers to engage with the material by posing a question about the generality of tensor transformations.
The video concludes with an invitation for viewers to share their thoughts and solutions in the comment section.
Transcripts
Browse More Related Video

Tensor Calculus 12c: The Self-Adjoint Property in Tensor Notation

Tensor Calculus For Physics Majors 002 | Vector Transformations and Vectors as Matrices

Tensor Calculus 3: The Jacobian

Tensor Calculus Lecture 12b: Inner Products in Tensor Notation
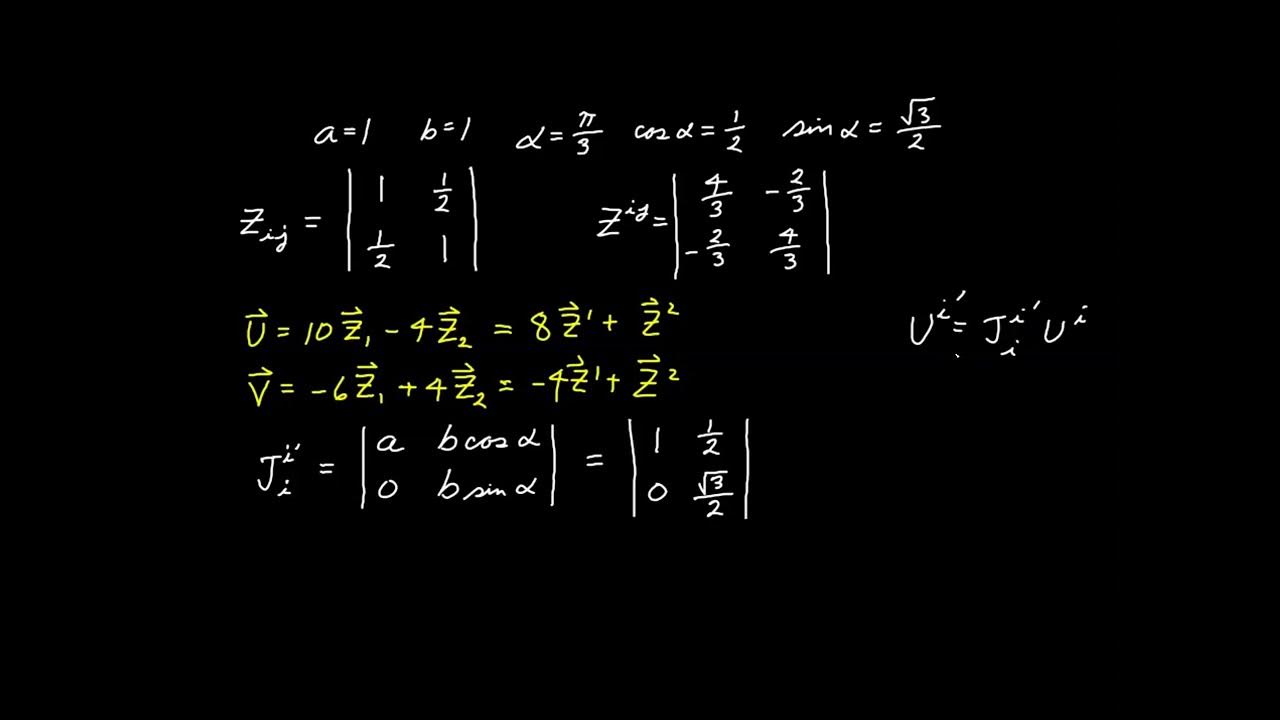
Video 26 - Vector Operation Examples

Tensors as a Sum of Symmetric and Antisymmetric Tensors
5.0 / 5 (0 votes)
Thanks for rating: