Tensors for Beginners 3: Vector Transformation Rules

eigenchris
10 Dec 201705:54
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the concept of vector components and their transformation relative to basis vectors. It explains why vector components behave in the opposite way to basis vectors when they are scaled or rotated. The script uses examples to illustrate this 'contra-variant' behavior, where increasing the size of the basis makes the components shrink, and a rotation of the basis results in a counter-rotation of the components. It concludes with a discussion on the notation used for contra-variant vector components and a preview of upcoming content on covectors and tensors.

Takeaways
  • 📚 The script discusses the concept of vector components transforming in the opposite way compared to the change in basis vectors.
  • 🔍 The example of increasing the size of the basis vectors by a factor of 2 demonstrates how vector components shrink by the same factor, maintaining the vector's invariant nature.
  • 📏 The script uses the analogy of 'measuring sticks' to explain why vector components appear to change size when the basis vectors are altered.
  • 🔄 The rotation of the basis vectors is contrasted with the rotation of vector components, showing that as the basis rotates one way, the components rotate the opposite way.
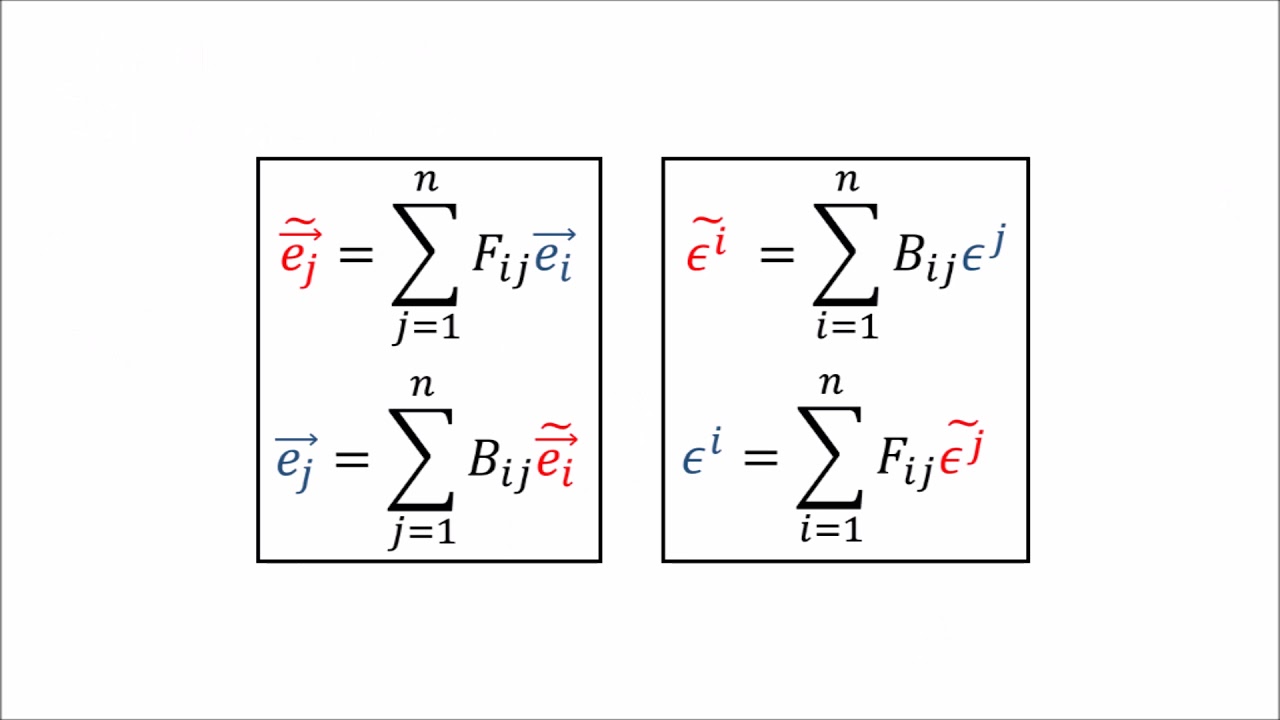
  • 📈 The script provides a mathematical proof to show that moving from old to new components involves using the backward transformation, and vice versa for the forward transformation.
  • 📝 The summation notation is used to express the vector V in terms of both old and new basis vectors, highlighting the relationship between the two sets of components.
  • 🧠 The concept of contra-variance is introduced, explaining that vector components are contra-variant tensors, which behave contrary to the basis vectors.
  • 📘 The script suggests a notation change for contra-variant components, placing the indices above the vector symbol to distinguish them from covariant basis indices.
  • 🤔 It addresses potential confusion between upper indices and exponents, reassuring that in the context of tensors, upper indices are typically vector indices.
  • 🚀 The video concludes with a teaser for upcoming content on covectors, another type of tensor, indicating a continuation of the discussion on tensor properties.
Q & A

  • Why do vector components transform in the opposite way compared to the basis vectors?

    -Vector components transform oppositely to the basis vectors to maintain the invariance of the vector itself. When the basis vectors change size or orientation, the components adjust in the opposite direction to ensure the vector's representation remains consistent.

  • What happens to the components of a vector when the basis vectors are doubled in size?

    -When the basis vectors are doubled in size, the components of the vector in the new basis are halved. This is because the larger basis vectors make the same vector appear smaller when measured in the new basis.

  • How does the rotation of the basis vectors affect the components of a vector?

    -When the basis vectors are rotated, the components of the vector rotate in the opposite direction. This is because the vector itself does not move, but the angles it makes with the new basis vectors change, affecting the perceived orientation of the vector.

  • What is the significance of the vector being invariant when discussing transformations?

    -The invariance of the vector means that its physical properties or its representation in space do not change, even though the basis vectors used to describe it do. This is crucial for maintaining the consistency of vector representations across different coordinate systems.

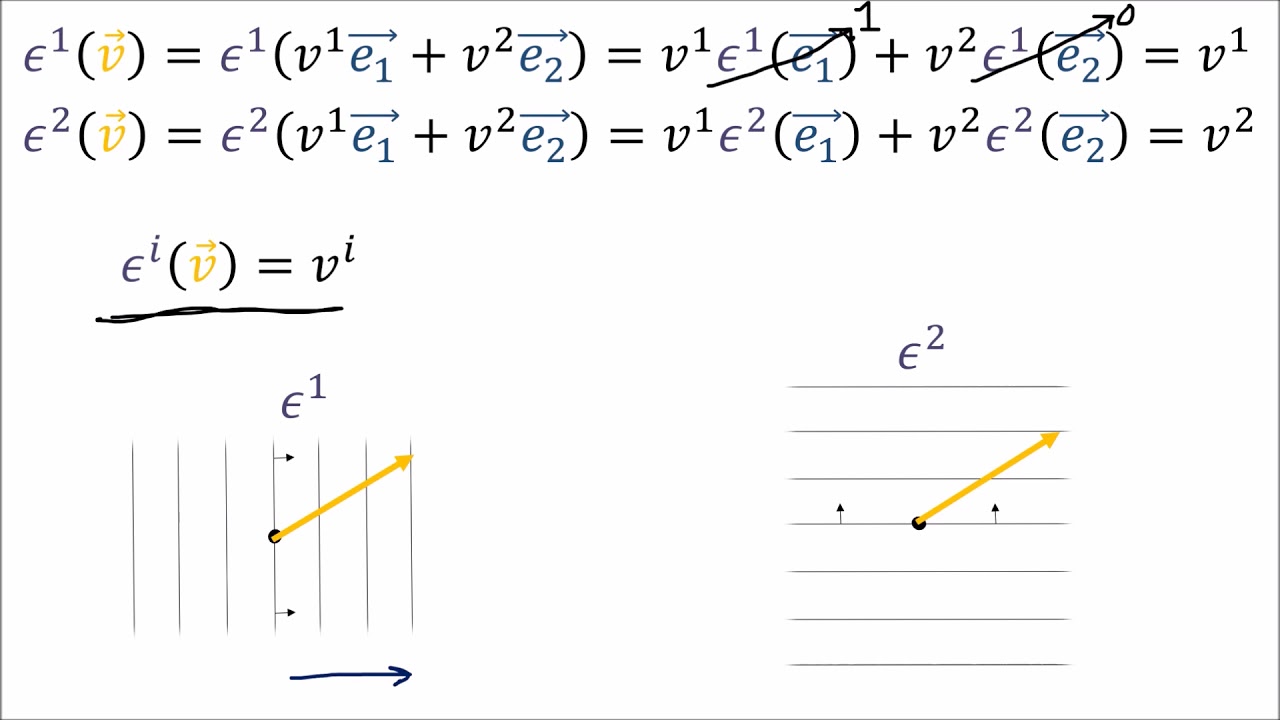
  • How can we express a vector V in terms of both old and new basis vectors?

    -A vector V can be expressed as a linear combination of both old and new basis vectors, with the coefficients being the respective old and new components. This is represented by two summations that are equal to V.

  • What is the purpose of using forward and backward transformations in the context of basis vectors?

    -Forward and backward transformations are used to convert between the old and new basis vectors, allowing us to express a vector in terms of either basis. They are essential for understanding how vectors and their components transform between different coordinate systems.

  • Why do we say that vector components are contra-variant?

    -Vector components are said to be contra-variant because they change in the opposite way to the basis vectors. This behavior is a key characteristic of contra-variant tensors, which include vectors.

  • What is the difference between a covector and a vector?

    -A covector is a type of tensor that is dual to a vector. While vectors transform contra-variantly with respect to changes in the basis, covectors transform co-variantly, meaning they change in the same way as the basis vectors.

  • Why are vector components written with indices above the V instead of below?

    -Writing the indices above the V serves as a reminder that vector components are contra-variant. This notation distinguishes them from the basis indices, which are typically written below, and helps to visually represent their opposite transformation behavior.

  • How can we avoid confusion between upper indices and exponents in tensor notation?

    -In tensor notation, upper indices are used to denote contra-variant components, while exponents are rarely used in tensor analysis. The context usually makes it clear whether an upper index represents a tensor index or an exponent, so confusion is minimal.

  • What is the next topic that will be discussed in the video series after vectors?

    -After discussing vectors, the video series will move on to discuss covectors, which are another example of a tensor and have different transformation properties compared to vectors.

Outlines
00:00
📚 Understanding Vector Transformation

This paragraph delves into the concept of vector transformation relative to basis changes. The script explains how vector components transform in the opposite direction to the basis vectors when the basis is scaled or rotated. The example given involves scaling the basis vectors by a factor of 2, which results in the vector components shrinking by the same factor, illustrating the concept of invariance of the vector itself. Another example discusses the rotation of the basis vectors and how it affects the components' orientation, demonstrating the counter-intuitive behavior of the components rotating in the opposite direction to the basis. The paragraph concludes with a general understanding that vector components are contra-variant, meaning they change in the opposite way to the basis vectors, and introduces the idea of proving this behavior in any dimension.

05:06
🔍 Contra-variant Vector Components and Tensor Notation

The second paragraph continues the discussion on vector components, focusing on their contra-variance and the notation used to represent them. It introduces the concept of contra-variant tensors and explains the significance of placing the vector component indices above the vector symbol, contrasting with the basis indices which are placed below. This notation serves as a reminder of their opposite behavior. The paragraph also addresses potential confusion with exponents but reassures that in the context of tensors, such confusion is unlikely. The summary concludes with a transition to the next topic, which is covectors, another type of tensor that will be discussed in subsequent videos.

Mindmap
Keywords
💡Vector Components
Vector components are the scalar values that describe the projection of a vector onto the axes of a coordinate system. In the video, the transformation of vector components is discussed in relation to changes in the basis vectors. When the basis vectors are scaled or rotated, the components of the vector transform in the opposite manner to maintain the vector's invariant nature. For instance, if the basis vectors are doubled in size, the components of the vector are halved, illustrating the concept of contravariance.
💡Basis Vectors
Basis vectors are the fundamental unit vectors in a vector space that define the directions of the coordinate axes. In the context of the video, the old and new basis vectors are used to describe the coordinate system in which a vector resides. Changes to these basis vectors, such as scaling or rotation, affect how the components of a vector are expressed within that system. For example, when the basis vectors are doubled, the components of the vector V in the new basis are [1/2, 1/2], showing the inverse relationship between basis vectors and vector components.
💡Contravariance
Contravariance is a property of tensors, including vectors, that describes how their components change in response to transformations of the coordinate system. In the video, it is explained that vector components are contravariant, meaning they transform in the opposite way to the basis vectors. This is demonstrated through the example of basis vectors being scaled or rotated, with the vector components adjusting accordingly to maintain the vector's magnitude and direction.
💡Tensors
Tensors are mathematical objects that generalize scalars, vectors, and other geometric entities. They describe linear relations between vectors and are used in fields such as physics and engineering. In the video, it is mentioned that vectors are contravariant tensors, indicating that their components change inversely to the transformations applied to the coordinate system. This concept is further elaborated upon with the notation change for vector components, placing indices above the vector symbol to denote contravariance.
💡Coordinate System
A coordinate system is a reference frame that specifies each point in a space by a set of numerical coordinates. In the video, the transformation of a vector's components is discussed within the context of an old and a new coordinate system defined by their respective basis vectors. The changes in the coordinate system's basis vectors lead to changes in the vector's components, demonstrating the importance of the coordinate system in vector representation.
💡Linear Combination
A linear combination is an expression constructed from two or more terms, where each term is a scalar multiple of a vector. In the video, the vector V is expressed as a linear combination of both the old and new basis vectors, with the coefficients being the respective components of the vector. This concept is crucial for understanding how vectors are represented in different coordinate systems and how their components transform.
💡Transformation
Transformation refers to a function that changes one mathematical object into another, often preserving certain properties. In the video, the forward and backward transformations are discussed in the context of changing from the old basis to the new basis, and vice versa. These transformations are essential for understanding how vector components adjust when the basis vectors are altered.
💡Invariant
An invariant is a property that remains unchanged under a given transformation. In the video, the vector V is described as invariant, meaning that despite changes in the coordinate system's basis vectors, the vector itself does not change. Instead, its components transform to reflect the new basis, maintaining the vector's original magnitude and direction.
💡Indices
In the context of tensors, indices are used to denote the components of a tensor and their position relative to the tensor. In the video, it is mentioned that the indices for vector components, which are contravariant, are written above the vector symbol, as opposed to the indices for basis vectors, which are covariant and written below. This notation helps distinguish between the two and indicates their different transformation behaviors.
💡Covectors
Covectors, also known as one-forms, are a type of tensor that are dual to vectors and transform in a covariant manner. While the video primarily discusses vectors and their contravariance, it mentions covector as another type of tensor that will be covered in subsequent videos. Covectors are relevant to the study of linear algebra and differential geometry, where they are used to take linear functionals of vectors.
Highlights

Explains the mystery of vector components transforming oppositely to the old and new bases.

Illustrates the concept with an old basis 'e_1, e_2' and a vector 'V' with components [1, 1].

Demonstrates the effect of increasing the size of the basis vectors by a factor of 2, causing vector components to shrink.

Introduces the idea that the vector 'V' remains invariant even as the basis vectors change.

Provides an example of rotating the basis vectors and the resulting change in the components of the vector 'V'.

Clarifies that the vector 'V' appears to rotate counterclockwise when the basis rotates clockwise due to the change in angles.

Discusses the intuition behind the opposite behavior of basis vectors and vector components in 2D.

Proposes to prove the opposite behavior of vector components in any dimension.

Presents two ways of writing vector 'V' using old and new basis vectors and their respective components.

Shows the use of backward transformation to move from old components to new components.

Explains the forward transformation used to go from new components to old components.

Summarizes the formulas for understanding how basis vectors and vector components transform.

Introduces the term 'contra-variant' to describe the behavior of vector components.

Announces the upcoming discussion on covectors as another example of a tensor.

Suggests a change in notation for vector components to indicate their contra-variance by placing indices above the 'V'.

Addresses potential confusion between upper indices and exponents in tensor notation.

Transcripts

Browse More Related Video

Tensors Explained Intuitively: Covariant, Contravariant, Rank

Tensors for Beginners 6: Covector Transformation Rules

Tensors for Beginners 5: Covector Components (Contains diagram error; see description)

Tensors for Beginners 8: Linear Map Transformation Rules

Introduction to Tensors

Tensor Calculus 5: Derivative Transformation Rules (Contravariance)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Vector TransformationBasis ChangeCoordinate SystemsLinear AlgebraContra-variantTensor TheoryMathematics EducationGeometric InterpretationComponent BehaviorEducational Content