Math 7 4 5 Homework Help Morgan

Mr. Morgan's Math Help

2 Nov 201833:41

EducationalLearning

32 Likes 10 Comments

TLDRThis Math 7 unit 4 lesson focuses on using decimals to express increases and decreases. It begins with an exploration of how calculators convert fractions to decimals, highlighting the differences between terminating and repeating decimals. The lesson then delves into working with repeating decimals, using long division to convert fractions into decimal form. It also covers comparing decimal values and understanding proportional relationships between quantities. The instructor uses creative analogies, such as wrestling matches, to explain division and introduces practical applications of decimals, like calculating heart rates and water consumption. Homework assignments reinforce the concepts learned, encouraging students to apply their knowledge to real-world scenarios.

Takeaways

😀 The lesson is focused on using decimals to describe increases and decreases.
🔢 Students learn how to convert fractions to decimal expansions using a calculator.
📚 The script discusses the decimal representation of fractions like one-half, one-third, and one-eleventh.
🤔 The difference between terminating decimals and repeating decimals is highlighted.
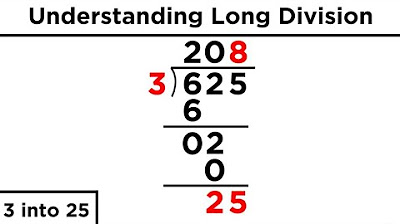
📉 The concept of long division is used to express fractions as decimals, with examples provided.
🏠 A wrestling analogy is used to explain the long division process, making it more relatable.
🔄 The script covers working with repeating decimals and how to identify them in division problems.
📈 The lesson includes matching diagrams with descriptions and equations to understand proportional relationships.
📘 The importance of understanding both fractions and decimals is emphasized for solving problems.
🏡 A real-life example of peanut butter consumption is used to demonstrate how to calculate decreases using decimals.
🏃‍♂️ The script concludes with an example about heart rates, showing how to determine if a rate is typical by converting beats per minute.

Q & A

What is the main topic of the Math 7 Unit 4 Lesson 5 video?
-The main topic of the lesson is working with decimals to describe increases and decreases, and converting fractions to decimal expansions using long division.
What is a common observation when dividing fractions by a calculator?
-A common observation is that some fractions result in a simple decimal that stops, like 1/2 which equals 0.5, while others result in a repeating decimal that seems to go on indefinitely, like 1/3 which equals 0.33333...
How does the instructor relate long division to wrestling in the classroom?
-The instructor uses a wrestling analogy where the person on top (the larger number) 'wins' and gets to live inside the house, while the person on the bottom (the smaller number) 'loses' and has to sleep outside. This helps students visualize the process of long division.
What is the decimal representation of 7 divided by 8 according to the video?
-The decimal representation of 7 divided by 8 is 0.875.
How does the video explain the concept of repeating decimals?
-The video explains repeating decimals by showing the long division process and pointing out how the same sequence of digits repeats after a certain point, such as in the division of 11 by 30 which results in a repeating decimal of 0.36.
What is the approximation of pi given in the video and how is it expressed as a decimal?
-The approximation of pi given in the video is 22 over 7. When expressed as a decimal, it is approximately 3.142857..., which is a repeating pattern.
How does the video use tape diagrams to illustrate proportional relationships?
-The video uses tape diagrams to visually represent increases and decreases in quantities. It matches each diagram with a description and an equation to show how the original value (x) changes to the new value (y).
What is the equation for a decrease by one-fourth in the context of the video?
-The equation for a decrease by one-fourth is y = 0.75x, where x is the original value and y is the new value after the decrease.
How does the video explain the process of converting fractions to decimals?
-The video explains the process by using long division to divide the numerator by the denominator of the fraction, then interpreting the result as a decimal, which may be a repeating or terminating decimal.
What is the significance of using both fractions and decimals in problem-solving according to the video?
-The significance is that both fractions and decimals have their uses and sometimes one is more convenient than the other. Being able to work with both allows for greater flexibility and problem-solving efficiency.
How does the video demonstrate the calculation of the amount of water a football team drank on a hot day?
-The video demonstrates that if the team drank 50 gallons and then half as much again, they would have consumed 75 gallons in total, using the fraction 3/2 times 50.
What is the equation for the number of times the heart beats in m minutes according to the video?
-The equation is h = 48m, where h represents the number of heartbeats and m represents the number of minutes.

Outlines

00:00

📚 Introduction to Decimals and Fractions

The script begins with an introduction to a math lesson focused on decimals, specifically unit fractions and their decimal expansions. The lesson starts with an exploration of how calculators represent fractions as decimals, noting the difference between terminating decimals like 1/2 (0.5) and repeating decimals like 1/3. The teacher uses a wrestling analogy to explain the concept of long division, demonstrating how to convert fractions like 7/8 into decimal form, emphasizing the process of division and how it leads to either terminating or repeating decimals.

05:01

🔢 Understanding Repeating Decimals

This paragraph delves deeper into repeating decimals, using the example of 1/3 to illustrate the concept of a repeating decimal. The teacher explains how to identify repeating patterns in division and convert them into a decimal form with a repeating bar. The lesson then compares different fractions and their decimal equivalents, highlighting the differences in their representations, such as the termination or repetition of digits. The teacher also discusses how to determine the greatest value among fractions represented as decimals.

10:03

📉 Visualizing Fractions and Decimals

The script continues with a practical application of the concepts learned, involving tape diagrams and proportional relationships. The teacher guides the students through matching diagrams with descriptions and equations, emphasizing the importance of understanding both fractions and decimals in problem-solving. The lesson also introduces the idea of increases and decreases in quantities, using visual representations to distinguish between them and how they can be represented mathematically.

15:03

📌 Equations and Proportional Relationships

In this section, the teacher discusses the relationship between equations and proportional relationships, focusing on how to represent these relationships mathematically. The lesson explains how to set up equations to represent increases and decreases, using the distributive property to simplify and express these relationships as equations involving decimals. The teacher provides examples of how to convert fractions to decimals within the context of these equations, reinforcing the connection between the mathematical concepts introduced earlier in the script.

20:05

📘 Applying Decimals to Word Problems

The script presents word problems that require the application of decimal operations, such as calculating the remaining amount of peanut butter after a family consumes a portion of it. The teacher demonstrates how to translate the word problem into a mathematical expression, emphasizing the use of decimals to represent fractions of quantities and how to perform calculations with them. The lesson also includes examples of calculating total consumption and comparing quantities using decimal representations.

25:05

🏋️‍♂️ Physical Applications of Decimals

This paragraph explores the application of decimals in real-world scenarios, such as calculating the water consumption of a football team and comparing heart rates. The teacher uses these examples to illustrate how decimals are used to measure and compare quantities in everyday situations. The lesson also includes a step-by-step guide on how to set up and solve these problems, emphasizing the importance of understanding proportional relationships and unit rates.

30:06

📚 Summary and Conclusion

The final paragraph of the script summarizes the lesson, highlighting the importance of understanding both fractions and decimals in mathematics. The teacher emphasizes the versatility of these mathematical tools and encourages students to practice working with both to enhance their problem-solving skills. The script concludes with a reminder of the lesson's key points and a prompt for students to apply what they've learned in their homework.

Mindmap

Keywords

💡Decimals

Decimals are a way of representing numbers using a base-10 system that includes digits to the right of a decimal point. In the video, decimals are used to express fractions and their equivalents, such as 0.875 for 7/8. They are also used to describe increases and decreases, making them a central concept in the lesson.

💡Fractions

Fractions are mathematical expressions that represent parts of a whole, typically written as a numerator (top number) divided by a denominator (bottom number). The video discusses converting fractions to decimals, such as 1/2 being equivalent to 0.5, and uses fractions to illustrate concepts of division and proportionality.

💡Long Division

Long division is a method of dividing two numbers, typically involving breaking down the dividend into multiples of the divisor. In the video, long division is used to convert fractions into decimal form, demonstrating how to find decimal expansions for unit fractions like 1/2 through 1/11.

💡Repeating Decimals

Repeating decimals are decimals where a sequence of digits repeats infinitely. The video mentions this concept when discussing the division of fractions like 1/3, which results in a non-terminating decimal (0.333...). Repeating decimals are a key part of understanding decimal expansions of fractions.

💡Proportional Relationships

Proportional relationships describe a constant ratio between two quantities. The video script uses proportional relationships to explain how changes in one quantity (e.g., an increase or decrease) affect another, often represented by equations like y = kx where k is the constant of proportionality.

💡Approximation

Approximation in the context of the video refers to the use of a fraction to estimate an irrational number, such as pi. The script mentions 22/7 as a common approximation for pi, illustrating how fractions can be used to get a close estimate of such numbers.

💡Tape Diagrams

Tape diagrams are visual representations used to solve problems involving fractions and proportional relationships. The video script describes using tape diagrams to match descriptions with equations, helping to visualize increases and decreases in quantities.

💡Equations

Equations in the video are used to represent mathematical relationships, particularly those involving proportionality. The script discusses equations like y = 0.75x to describe decreases or y = 1.25x for increases, showing how these equations can be derived from proportional relationships.

💡Increases and Decreases

Increases and decreases are changes in quantity, often described as a fraction or decimal of the original amount. The video script uses these terms to discuss how quantities can be increased or decreased by a certain fraction, such as increasing by one-fourth or decreasing by two-fifths.

💡Constant Proportionality

Constant proportionality is a concept where the ratio between two quantities remains the same. In the video, this is used to set up equations that describe how one quantity changes in relation to another, such as heart rate in relation to time.

Highlights

Introduction to using decimals to describe increases and decreases.

Explanation of how calculators convert fractions to decimal expansions.

Demonstration of the difference between terminating and repeating decimals.

Teaching method using wrestling as an analogy for understanding fractions and division.

Long division technique to convert fractions into decimal form.

Conversion of fractions like 7/8, 2/5, and 11/30 into decimal equivalents.

Identification of the greatest value among fractions using decimal representation.

Approximation of pi using the fraction 22/7 and its decimal conversion.

Matching tape diagrams with proportional relationships in descriptions and equations.

Creating equations to represent increases and decreases in fractions of quantities.

Practical application: calculating remaining peanut butter in the pantry after consumption.

Understanding how to determine if a heart rate is typical based on given parameters.

Setting up equations to represent the relationship between heart beats and time.

Importance of being able to work with both fractions and decimals in mathematical problems.

Homework assignment integrating concepts of fractions, decimals, and proportional relationships.

Summary of the lesson emphasizing the utility of long division in finding decimal expressions for fractions.

Transcripts

Browse More Related Video

Repeating decimal as infinite geometric series | Precalculus | Khan Academy

Converting Between Fractions, Decimals, and Percentages

Division of Large Numbers: Long Division

Decimals to Fractions

Basic Math Review

Math Antics - What Are Percentages?

Related Tags

Decimals Fractions Mathematics Education Long Division Approximation Pi Homework Help Teaching Method Numerical Concepts