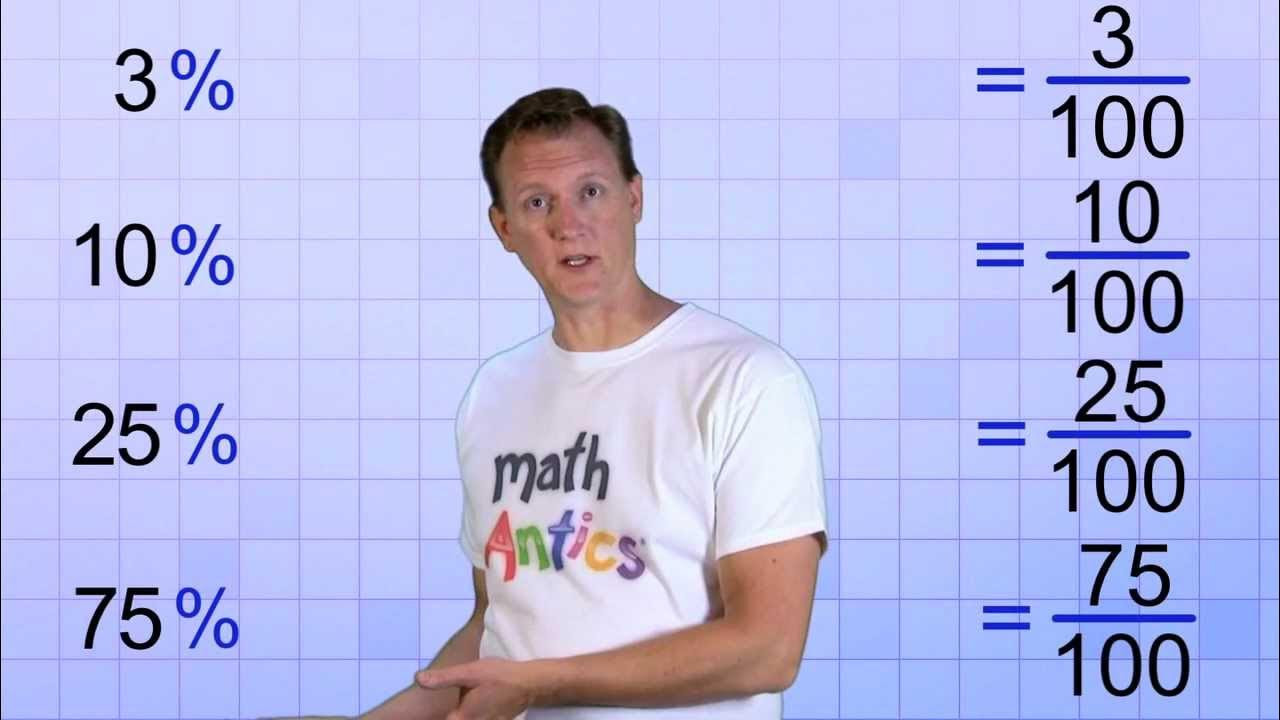Converting Between Fractions, Decimals, and Percentages
TLDRThe script explains how to convert between fractions, decimals, and percentages, which are different ways to represent the same values. It provides tips like crossing out zeros when reducing fractions and moving the decimal place to convert between percents and decimals. Examples are shown such as converting 30% to 0.3 and calculating sales tax. A table shows common fraction-decimal-percent equivalents. Finally, an practice problem has the viewer arrange 45%, 21/50, and 0.43 from least to greatest, requiring conversion between formats, and the solution is explained.
Takeaways
- 😀 You can convert between fractions, decimals, and percentages since they represent the same value.
- 😎 To convert a percentage to a fraction, set it over 100. 30% becomes 30/100.
- 🤓 To convert a fraction to a decimal, divide the numerator by the denominator. 3/10 = 0.3.
- 🧐 To directly convert a percentage to a decimal, move the decimal point 2 places left.
- 🤯 A shortcut to reduce fractions is to cross out common zeros when dividing both numbers by 10.
- 😮 To convert a decimal to a percentage, move the decimal point 2 places right.
- 🤔 To convert a fraction to a percentage, first convert it to a decimal, then move the decimal 2 places right.
- 👍 Arrange fractions with a common denominator to easily compare their values.
- ✨ A table of common fraction/decimal/percentage equivalents helps with conversions.
- 🦾 Practice converting between formats to improve comprehension and math skills.
Q & A
What are the three main ways to represent numbers that are discussed?
-The three main ways to represent numbers discussed are fractions, decimals, and percentages.
How can you convert a percentage to a fraction?
-To convert a percentage to a fraction, make the percentage the numerator and 100 the denominator. For example, 30% becomes 30/100.
What is the quick trick for converting a percentage to a decimal?
-The quick trick is to move the decimal point two places to the left. For example, 30% becomes 0.30.
How do you calculate sales tax using a decimal percentage?
-Multiply the price of the item by the decimal percentage. For example, if an item costs $50 and the tax rate is 8.25%, multiply $50 by 0.0825.
How do you convert a decimal to a percentage?
-Move the decimal point two places to the right. For example, 0.84 becomes 84%.
How can you convert a fraction to a percentage?
-First convert the fraction to a decimal, then move the decimal point two places to the right. For example, 3/5 = 0.6 = 60%.
What is the purpose of the conversion table provided?
-The conversion table allows for easy reference between common fractions, decimals, and percentages. It helps cement the relationships between these representations.
What process is used to order fractions from least to greatest?
-First convert all fractions to have a common denominator, usually 100. Then the numerators can be directly compared to put them in order.
Why is it useful to be able to convert between different number representations?
-Being able to convert between fractions, decimals, and percentages makes it easier to compare values and perform calculations using the most convenient representation.
What are some examples of when different number representations are most useful?
-Fractions are useful for ratios and parts of a whole, decimals for more precise values, and percentages to represent partial amounts out of 100.
Outlines
😀 Converting Between Fractions, Decimals and Percentages
This paragraph introduces the concepts of fractions, decimals, and percentages and how they can represent the same values. It then provides step-by-step examples of converting 30% to a fraction and decimal, and converting a decimal sales tax rate to a percentage. Tips are given, like moving the decimal place twice between percents and decimals, and being able to cancel zeros when converting fractions.
Mindmap
Keywords
💡fractions
💡decimals
💡percentages
💡converting
💡equivalent
💡compare
💡multiply
💡denominator
💡place value
💡order
Highlights
We've learned about fractions, decimals, and percentages and seen how we can use any of these to represent the same value, so we can certainly convert between them.
When converting percentages to decimals, move the decimal place two places left because 100 is two orders of magnitude greater than 1.
To convert a decimal to a percentage, move the decimal point two places to the right, which multiplies by 100.
To convert a fraction to a percentage, first convert it to a decimal, then move the decimal point two places right.
Here is a table showing common fractions, decimals, and percentages for easy conversion between these forms.
Let's arrange 0.43, 45%, and 21/50 from least to greatest. First convert everything to fractions with denominator 100.
42/100 comes first, then 43/100, then 45/100. So the order is 21/50, 0.43, 45%.
When converting a percentage to a fraction, the denominator is always 100.
To reduce a fraction, divide both parts by a common factor. For example, divide by 10 to reduce 30/100 to 3/10.
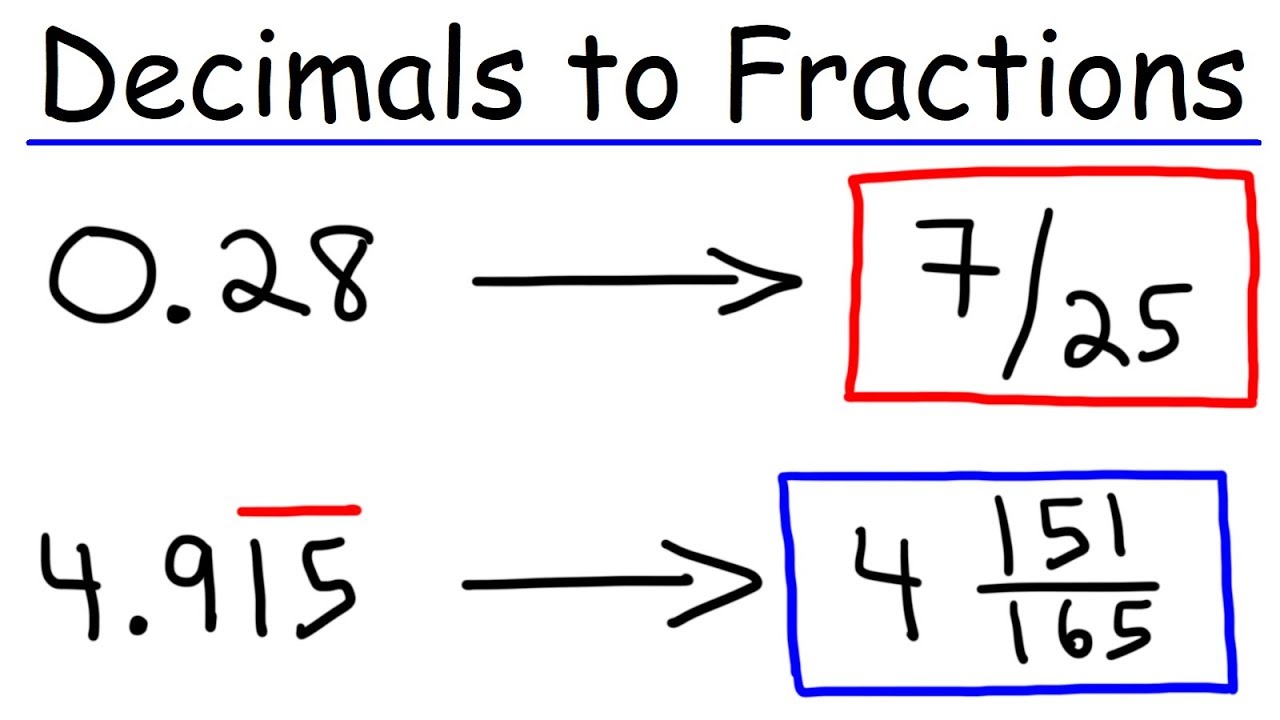
To convert a decimal to a fraction, determine what place value each digit represents.
Percentages can easily represent sales tax rates. To calculate tax, multiply the price by the decimal percentage.
Being able to interchange fractions, decimals, and percentages allows using whichever form fits the context best.
Arranging values from least to greatest is easier when they are expressed in comparable forms like fractions over 100.
Hot tips are provided for quick mental conversions between percentage, decimal, and fraction forms.
Practice questions and comprehension checks reinforce the concepts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: