Calculus Polar Area Rose Curve Example

turksvids
14 Dec 201303:04
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script demonstrates the process of finding the area of a petal on a rose curve with the equation R = cos(3θ) using calculus. It emphasizes the importance of graphing the polar curve to understand its pattern and symmetry. The script guides through calculating half the petal's area by integrating from θ = 0 to π/6, simplifying the expression using trigonometric identities, and doubling the result due to symmetry. It also touches on finding the entire area for three petals and offers a helpful alternative approach for the calculation, making it an insightful resource for those learning polar coordinates and calculus.

Takeaways
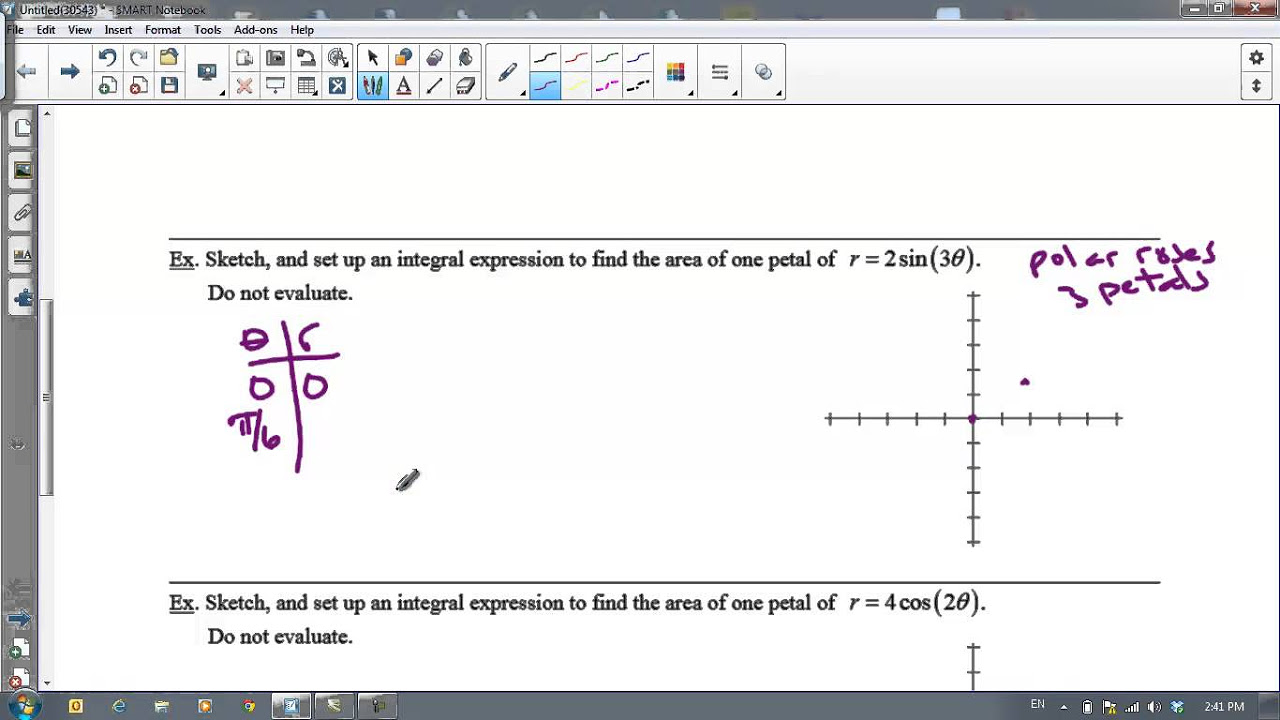
  • 📚 The video discusses finding the polar area of a rose curve, specifically for the equation \( R = \cos(3\theta) \).
  • 📈 The first step is to graph the rose curve, which involves finding where \( R = 0 \) and sketching those lines.
  • 🔍 The graph is analyzed in the rectangular coordinate system to understand the pattern and trace the polar curve.
  • 🌹 The area of interest is one petal of the rose curve, which is half of a petal due to symmetry.
  • 🔢 The formula for polar area involves integrating \( \frac{1}{2}R^2 \) with respect to \( \theta \).
  • 📉 The integration starts at \( \theta = 0 \) and stops at \( \theta = \frac{\pi}{6} \), where \( R \) first reaches zero.
  • 🧮 The integral involves squaring the radius function \( \cos(3\theta) \) and integrating with respect to \( \theta \).
  • 📊 The area calculation can be simplified by using trigonometric identities, such as the double angle formula for cosine squared.
  • 🔄 An alternative approach is to integrate from \( -\frac{\pi}{6} \) to \( \frac{\pi}{6} \) to cover the entire petal, leveraging the symmetry of the curve.
  • 🌐 To find the area of the entire region enclosed by the rose curve, multiply the area of one petal by three, as there are three petals in total.
Q & A

  • What is the main topic of the video script?

    -The main topic of the video script is finding the polar area of one petal of a rose curve defined by the equation R = cos(3θ) using calculus.

  • What is the first step suggested in the script to approach the problem?

    -The first step suggested is to graph the rose curve in polar coordinates, specifically finding where R equals 0 and sketching those lines.

  • How does the script suggest using symmetry to simplify the calculation of the polar area?

    -The script suggests finding half of the petal's area and then using symmetry to double the result, as the formula for polar area already includes a factor of 1/2.

  • What is the range of θ for the integral when calculating the area of half a petal of the rose curve?

    -The range of θ for the integral is from 0 to π/6, as this is the interval where the rose curve completes half a petal before the radius R becomes zero again.

  • What is the integral expression used to calculate the area of half a petal of the rose curve?

    -The integral expression is ∫ from 0 to π/6 of (cos(3θ))^2 dθ.

  • Why does the script mention using a calculator for the integral calculation?

    -The script mentions using a calculator to simplify the process and avoid manual computation, which can be complex and prone to errors.

  • What is the result of the integral calculation for the area of half a petal as mentioned in the script?

    -The result of the integral calculation for the area of half a petal is π/12.

  • How does the script suggest simplifying the integral using trigonometric identities?

    -The script suggests using the double angle formula or power reducing formula to simplify (cos(3θ))^2 to 1 + cos(6θ).

  • What alternative method is presented in the script for calculating the area of a petal?

    -The alternative method presented is to integrate from -π/6 to π/6, which covers both the bottom and top halves of the petal, and then calculate the area.

  • If the entire area enclosed by the rose curve is desired, how does the script suggest finding it?

    -The script suggests multiplying the area of one petal by three, since there are three petals in the rose curve defined by R = cos(3θ).

Outlines
00:00
📚 Calculus in Finding Polar Area of a Rose Curve

The script introduces a calculus example to find the area of one petal of a rose curve defined by the polar equation R = cos(3θ). The process begins with graphing the curve and identifying where R equals zero to sketch the petal's boundary. The focus is on finding the area of half a petal due to symmetry, which simplifies the calculation. The area calculation involves setting up an integral from θ = 0 to θ = π/6, squaring the radius function, and integrating with respect to θ. The script mentions using a calculator for the actual computation and provides a hint about simplifying the integral using trigonometric identities, such as the double angle formula for cosine squared.

Mindmap
Keywords
💡Polar Area
Polar Area refers to the area of a region defined in polar coordinates, where the position of points is determined by their distance from the origin (radius) and the angle they make with the positive x-axis (theta). In the video, the concept is used to calculate the area of a petal of a rose curve, emphasizing the importance of understanding polar coordinates in solving such problems.
💡Rose Curve
A rose curve is a type of polar curve defined by an equation of the form r = a sin(nθ) or r = a cos(nθ), where a is a constant and n is an integer. These curves resemble roses when plotted in polar coordinates. The video script discusses finding the area of one petal of a rose curve defined by r = cos(3θ), highlighting the specific characteristics of this type of curve.
💡Graphing
Graphing in the context of the video refers to the process of visually representing the mathematical relationship between radius r and angle θ in polar coordinates. The script mentions graphing the rose curve to understand where r equals zero, which is crucial for determining the boundaries of the area to be calculated.
💡Symmetry
Symmetry in this context is a mathematical property that allows the simplification of calculations by focusing on a part of a figure and then multiplying the result by the number of symmetrical parts. The video script uses symmetry to find half of the petal's area and then doubles it to get the total area, demonstrating a common technique in polar coordinate problems.
💡Polar Coordinates
Polar coordinates are a two-dimensional coordinate system where each point is defined by its distance from the origin (radius) and the angle it makes with the positive x-axis (theta). The video script uses polar coordinates to describe the rose curve and calculate the area, emphasizing the fundamental role of this system in the problem-solving process.
💡Integral
In the video, an integral is used to calculate the area under the curve in polar coordinates. The script specifically mentions integrating (1/2) r^2 with respect to θ from 0 to (π/6) to find the area of half a petal, illustrating the application of calculus in determining areas in polar coordinates.
💡Cosine of 3 Theta
The term 'cosine of 3 theta' is part of the equation defining the rose curve in the video. It represents the radius r as a function of the angle θ, where r = cos(3θ). This equation is crucial for graphing the curve and calculating the area of its petals.
💡Double Angle Formula
The double angle formula is a trigonometric identity used in the video to simplify the expression cos^2(3θ). The script mentions using this formula to express cos^2(3θ) as (1 + cos(6θ))/2, which is essential for evaluating the integral and finding the area.
💡Pi Over Six
In the script, (π/6) is a specific angle where the radius r of the rose curve equals zero, marking the boundary of one petal. The video uses this angle to define the limits of integration when calculating the area of half a petal.
💡Three Petals
The concept of 'three petals' in the video refers to the total number of petals in the rose curve when the curve is fully traced. The script mentions that since one petal's area has been calculated, multiplying this by three gives the area of the entire region enclosed by the rose curve, demonstrating the use of symmetry in the calculation.
Highlights

Introduction to finding polar area using calculus for a rose curve.

Problem statement: Find the area of one petal of R = cos(3θ).

Explanation of graphing a rose curve in polar coordinates.

Identifying where R equals zero to sketch the graph.

Using symmetry to simplify the area calculation.

Deciding to calculate half of the petal area and then doubling it.

Starting the integral at θ = 0 and stopping at θ = π/6.

Expression for the integral: 1/2 ∫(R^2) dθ.

Substituting R = cos(3θ) into the integral.

Using a calculator to compute the integral.

Result of the calculation: Area = π/12.

Mention of using trigonometric identities to simplify the integral.

Alternative method by starting the integral at -π/6.

Explanation of how the integral from -π/6 to π/6 covers one petal.

Multiplying the area of one petal by three to find the total area of the rose curve.

Summary of the process for dealing with rose curves in polar coordinates.

Encouragement and well wishes for the audience.

Transcripts

Browse More Related Video

Notes on Polar, Day 3

Graph of r = 1 + cos(theta/2) | MIT 18.01SC Single Variable Calculus, Fall 2010

Area Bounded by a Polar Curve

Calculus Polar Area Limacon Example

Finding Slope of a Polar Curve in Calculus

Calculus Polar Area Region Between Curves Example

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusPolar AreaRose CurveCosine FunctionGraphingSymmetryIntegralsDouble AnglePolar CoordinatesArea Calculation