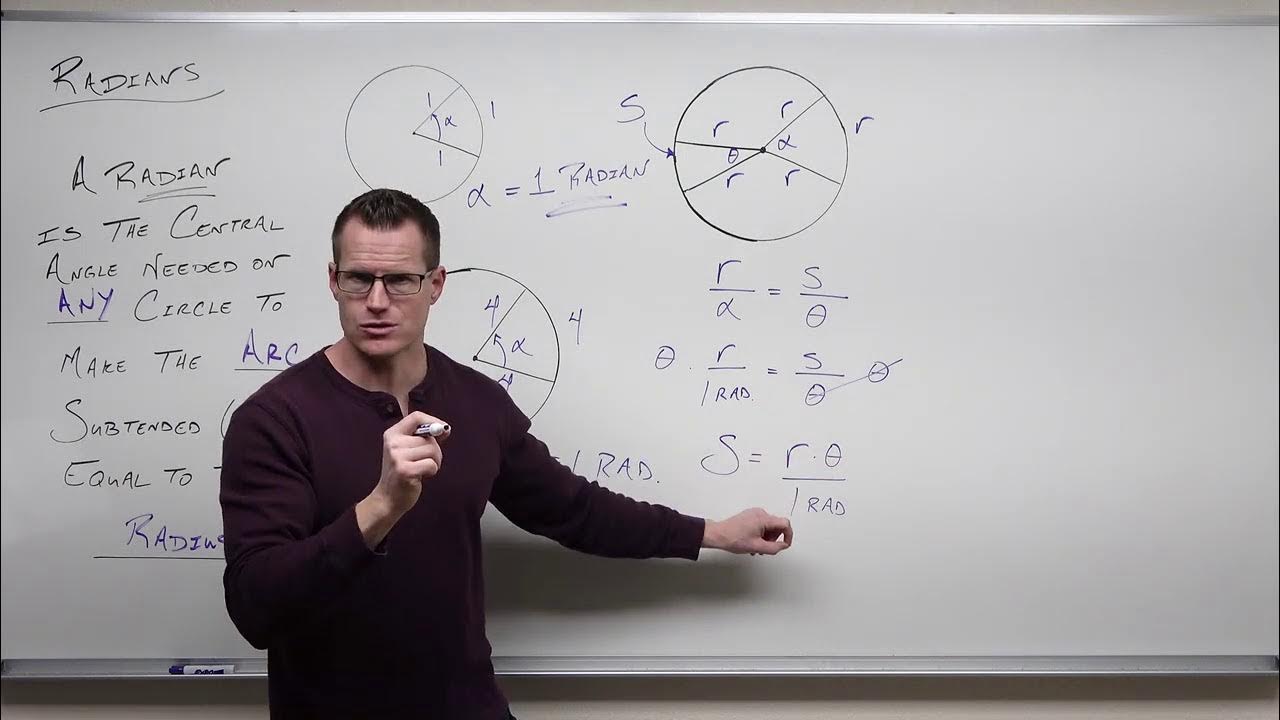Arc Length of a Circle Formula - Sector Area, Examples, Radians, In Terms of Pi, Trigonometry
TLDRThis educational video script explains how to calculate arc length and sector area of a circle. It introduces the formula for arc length as the product of the angle in radians and the radius (s = Θ * R), and demonstrates its application with examples, including converting degrees to radians. The script also covers two methods for finding the area of a sector: one using radians (A = 1/2 Θ * R^2) and another using degrees (A = Θ/360 * π * R^2). It emphasizes the relationship between these formulas and their practical use in geometry, concluding with an invitation to access a comprehensive trigonometry course online.
Takeaways
- 📐 The arc length (s) of a circle is the length of a segment of the circle's circumference and is determined by the angle (Theta) in radians and the radius (R).
- 🔢 The formula to calculate arc length is \( s = \Theta \times R \), where Theta is in radians and R is the radius of the circle.
- 🌀 A full circle is 6.28 radians, and half a circle is 3.14 radians, which helps to understand the proportion of the circle covered by a given angle.
- 📏 To find the arc length when the angle is given in degrees, convert the angle to radians by multiplying the degree measure by \( \frac{\pi}{180} \).
- 📐 An alternative formula for arc length when the angle is in degrees is \( s = \frac{\Theta}{360} \times 2\pi R \), where Theta is the angle in degrees.
- 🔴 The area of a sector of a circle can be calculated using the formula \( \frac{1}{2} \Theta R^2 \) when the angle is given in radians.
- 🟠 If the angle for the sector area is in degrees, the formula becomes \( \frac{\Theta}{360} \times \pi R^2 \), representing the fraction of the circle's area that the sector occupies.
- 📐 The relationship between the arc length and the area of a sector is that both are calculated based on the fraction of the circle's total circumference or area.
- 📚 The script provides examples and a step-by-step explanation of how to calculate arc length and sector area using both radians and degrees.
- 📘 The video also mentions an online trigonometry course available at emi.com for those who want to learn more about trigonometry topics.
Q & A
What is the definition of arc length in the context of a circle?
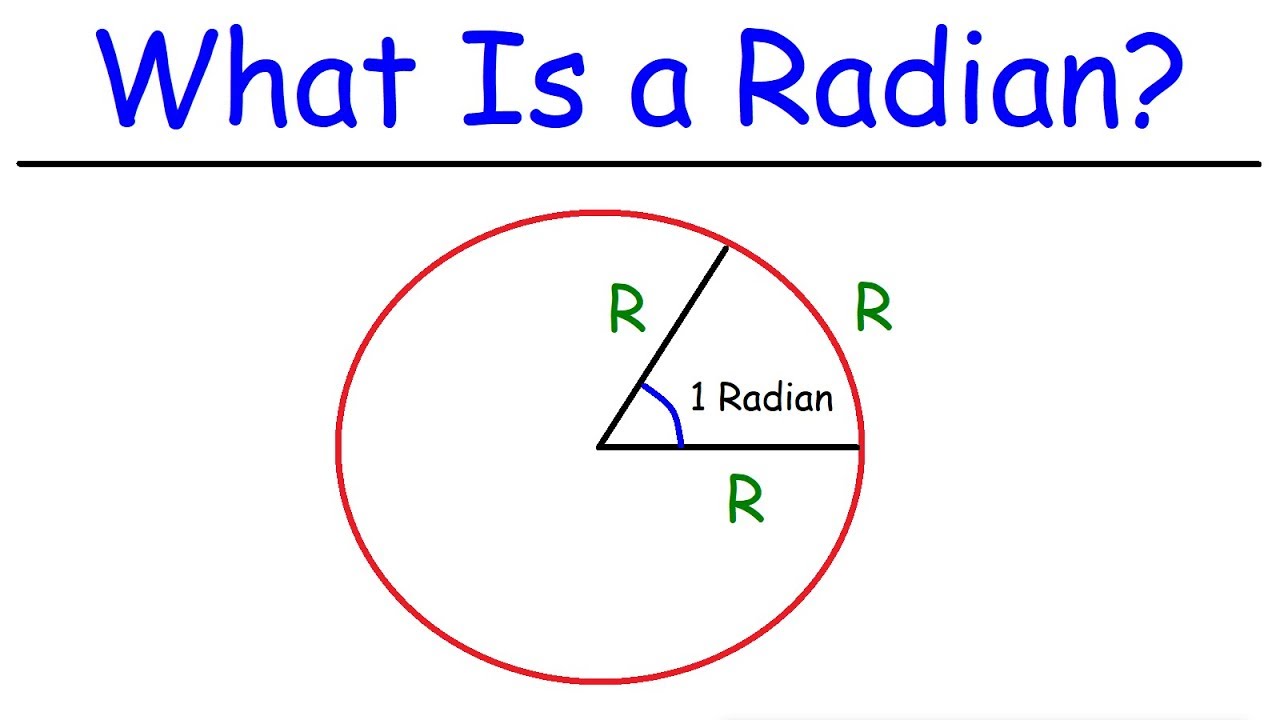
-Arc length, denoted as 's' in the script, refers to the length of a segment of a circle's circumference. It is determined by the central angle (in radians) that subtends the arc and the radius of the circle.
How is the arc length of a circle calculated when the angle is given in radians?
-The arc length is calculated by multiplying the radius (R) of the circle by the angle (Theta) in radians. The formula used is s = Theta * R.
Can you provide an example of calculating arc length with an angle in radians?
-Sure, if the angle is 5 radians and the radius is 12T, the arc length (s) would be 5 * 12T = 60T feet.
How do you convert an angle from degrees to radians?
-To convert an angle from degrees to radians, you multiply the degree measure by Pi and then divide by 180. The formula is radians = (Pi * degrees) / 180.
What is the arc length if the radius is 8 cm and the angle is 150°?
-First, convert 150° to radians: 150° * (Pi / 180) = 5Pi/6 radians. Then, calculate the arc length using the formula s = Theta * R, which gives s = 5Pi/6 * 8 cm = 40Pi/6 cm, which simplifies to approximately 20.94 cm.
What is an alternative method to calculate arc length when the angle is in degrees?
-An alternative method is to use the formula s = (angle in degrees / 360) * 2 * Pi * R, where R is the radius of the circle.
How does the circumference of a circle relate to the arc length?
-The circumference of a circle (2 * Pi * R) represents the total length around the circle. The arc length is a fraction of this circumference, corresponding to the fraction of the circle's angle.
What is the formula to calculate the area of a sector of a circle when the angle is in radians?
-The formula to calculate the area of a sector when the angle is in radians is A = (1/2) * Theta * R^2.
How can you find the area of a sector if the angle is given in degrees?
-If the angle is in degrees, you can find the area of a sector using the formula A = (Theta / 360) * Pi * R^2.
Can you provide an example of calculating the area of a sector with an angle in degrees?
-Yes, for a 60° angle and a radius of 5T, the area of the sector would be (60 / 360) * Pi * (5T)^2 = 25Pi / 6 square units.
How is the area of a sector related to the entire area of the circle?
-The area of a sector is the fraction of the entire area of the circle that is subtended by the sector's central angle. It is calculated as the fraction of the circle (Theta / 360) times the total area of the circle (Pi * R^2).
Outlines
📐 Understanding Arc Length in Circles
This paragraph introduces the concept of arc length in a circle and explains how to calculate it. It starts with a visual description of an arc segment within a circle and defines the arc length 's' as the distance along the circle between two points A and B, based on the angle Theta. The relationship between arc length, the radius of the circle, and the angle in radians is established, with the formula s = Theta * R. Two examples are provided to illustrate the calculation: the first with an angle of 5 radians and a radius of 12T, resulting in an arc length of 60 feet; the second with a radius of 8 cm and an angle of 150°, which requires converting degrees to radians and results in an arc length of approximately 20.944 cm. An alternative method is also mentioned for calculating arc length using the angle in degrees, which involves the formula s = (angle in degrees / 360) * 2πR.
🔍 Calculating Sector Area and Arc Length from Circles
The second paragraph delves into the calculation of the area of a sector of a circle and the arc length as a fraction of the circle's circumference. It explains that the arc length can be thought of as the circumference times a fraction of the circle, represented by Theta over 360. The paragraph provides a step-by-step solution for finding the arc length when the angle is given in degrees, using the formula (angle in degrees / 360) * 2πR, and demonstrates this with an example of a 150° angle and an 8 cm radius, yielding an arc length of approximately 20.944 cm. The area of a sector is then discussed, with the formula A = (1/2) * Theta * R^2 for angles in radians, and its conversion for angles in degrees, A = (Theta / 360) * πR^2. Examples are given to show how to calculate the area of sectors for both radians and degrees, emphasizing the relationship between the sector's area, the circle's area, and the angle's fraction of the circle.
📏 Sector Area Calculation with Radians and Degrees
This paragraph continues the discussion on calculating the area of a sector in a circle, focusing on the use of radians and degrees. It provides the formula for sector area when the angle is in radians, A = (1/2) * Theta * R^2, and shows its application with an example of a 90° angle and a 10 cm radius, resulting in an area of 25π square cm. The paragraph also explains how to convert the radians-based formula to one that uses degrees by multiplying by 2π/360, leading to the formula A = (Theta / 360) * πR^2. The similarities between the processes of finding arc length and sector area are highlighted, showing how both can be derived from the original formula by adjusting for the angle's unit. Additional examples are given, including one with a 60° angle and a 5T radius, resulting in an area of approximately 13.1 square feet, and another with a 2 radian angle and an 8 cm radius, yielding an area of 64 square cm.
📐 Final Thoughts on Sector Area Calculation
The final paragraph succinctly wraps up the topic by reiterating the formulas for calculating the area of a sector when the angle is given in radians or degrees. It emphasizes the straightforward calculation of the sector area as 64 square cm for an angle of two radians and a radius of 8 cm. The paragraph serves as a brief conclusion to the detailed explanations and examples provided in the previous sections, reinforcing the understanding of sector area calculation in the context of circle geometry.
Mindmap
Keywords
💡Arc Length
💡Radians
💡Radius
💡Angle Theta
💡Circumference
💡Degrees
💡Sector Area
💡Unit Circle
💡Trigonometry
💡Online Course
Highlights
Introduction to the concept of arc length and its calculation based on the angle Theta.
Explanation of the relationship between arc length (s), the radius (r), and the angle in radians.
Example calculation of arc length with an angle of 5 radians and a radius of 12T.
Conversion of radians to understand angles in terms of a full circle and half a circle.
Second example with a radius of 8 cm and an angle given in degrees (150°).
Conversion of degrees to radians using the formula (Theta * Pi / 180).
Calculation of arc length using the formula Theta * R for angles in radians.
Alternative method for calculating arc length when the angle is given in degrees.
Explanation of the relationship between arc length and the circumference of a circle.
Introduction to the concept of sector area calculation in a circle.
Formula for calculating the area of a sector when the angle is in radians: (1/2 * Theta * R^2).
Conversion of the sector area formula to accommodate angles given in degrees.
Example calculation of sector area with an angle of 90° and a radius of 10 cm.
Understanding of the sector area as a fraction of the total circle area.
Similarities between the formulas for arc length and sector area calculation.
Final example calculating sector area with an angle of 60° and a radius of 5T.
Conversion of the sector area formula result to a decimal value for practical applications.
Additional example with an angle in radians (2 radians) and a radius of 8 cm for sector area calculation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: