Disk Washer Method to Find the Volume of Solids of Revolution | Calculus 2

Quoc Dat Phung

15 Oct 202265:07

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script delves into the concept of solids of revolution, explaining how three-dimensional objects are created by rotating two-dimensional areas around an axis. It provides step-by-step solutions for finding the volume of these solids, using integral calculus to calculate the area of circular cross-sections and emphasizing the importance of correctly setting up and evaluating the integrals. The script covers various examples, including rotation around the x and y-axes and around vertical lines to the left and right of the y-axis, simplifying the complex process into manageable steps.

Takeaways

📚 Solids of Revolution are three-dimensional objects created by rotating a two-dimensional area around an axis.
🔄 The process involves integrating the area of circular cross-sections to find the volume of the solid formed after rotation.
⭕ The area of a circular cross-section is given by Pi times the radius squared, which is derived from the function being rotated.
📉 For functions rotated around the x-axis, the radius is often expressed in terms of x, and for y-axis rotation, in terms of y.
📌 The volume formula for solids of revolution is V = the integral from A to B of (area of cross-section) dX or dY, depending on the axis of rotation.
📐 The radius for the cross-section can be determined by the difference between the outer and inner function values when dealing with areas between curves.
🔢 The actual volume calculation involves evaluating the integral with the correct limits, often from 0 to a certain value.
📈 Examples provided demonstrate solids created by rotating simple functions like Y = X, Y = X^2, and Y = X^(1/3) around various axes.
🧩 Each example breaks down the process of finding the area of the cross-section, setting up the integral, and calculating the volume.
🔑 Key to solving these problems is substituting the radius in terms of the variable of integration and simplifying the resulting expressions before integrating.
📝 The final step is always to evaluate the integral within the given limits and simplify the expression to find the volume of the solid.

Q & A

What is a solid of revolution?
-A solid of revolution is a three-dimensional object created by rotating a two-dimensional area around an axis, typically the x or y-axis in a Cartesian coordinate system.
How do you calculate the volume of a solid of revolution?
-The volume of a solid of revolution is calculated using the formula V = the integral from A to B of π times the square of the radius function with respect to the axis of rotation.
What is the radius function in the context of solids of revolution?
-The radius function represents the distance from the axis of rotation to the curve that forms the cross-section of the solid. It is usually expressed in terms of the variable associated with the axis of rotation.
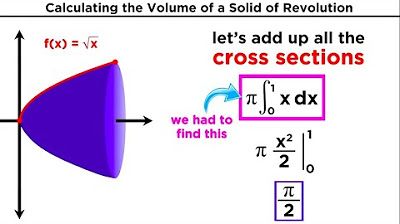
In the script, how is the volume of the solid formed by rotating y = √x around the x-axis from x = 0 to x = 1 calculated?
-The volume is found by integrating π times x from 0 to 1, where x is the radius function for the given rotation, resulting in π times (1/2) times 1^2, which simplifies to π/2.
What is the significance of the antiderivative in calculating the volume of solids of revolution?
-The antiderivative is used to evaluate the definite integral that represents the volume of the solid. It provides the accumulated volume under the curve from the lower to the upper limit of integration.
How does the shape of the solid change when the function rotated is different?
-The shape of the solid changes depending on the curve of the function being rotated. Different functions result in different cross-sectional shapes and sizes, leading to various solid geometries.
In the script, what is the volume of the solid formed by rotating the area between y = x and y = x^2 around the x-axis?
-The volume is calculated by subtracting the volume of the solid formed by y = x^2 from the volume of the solid formed by y = x, resulting in π times the integral from 0 to 1 of (x^2 - x^4) dx, which simplifies to 5π/14.
Why is it necessary to subtract the volume of the inner function when calculating the volume of a solid between two functions?
-Subtracting the volume of the inner function from the volume of the outer function eliminates the empty space inside the solid, providing the net volume of the actual material contained within the solid.
What is the role of the boundaries in the integral when calculating the volume of a solid of revolution?
-The boundaries of the integral define the limits of rotation along the axis, ensuring that the volume calculation is specific to the region of interest between these limits.
How does rotating a function around a vertical line to the left of the y-axis affect the volume calculation?
-Rotating around a vertical line to the left of the y-axis requires adjusting the radius function to account for the distance from the y-axis to the function, which may involve rewriting the function in terms of the new variable associated with the axis of rotation.
In the script, what is the volume of the solid obtained by rotating the area bounded by y = x^(1/3) and y = x^2 around the line y = -1?
-The volume is calculated by integrating the difference of the areas of the two circular cross-sections formed by the functions y = x^(1/3) and y = x^2, with respect to y, from y = -1 to y = 0, resulting in π/2.

Outlines

00:00

📚 Introduction to Solids of Revolution

This paragraph introduces the concept of solids of revolution, explaining that they are three-dimensional objects formed by rotating a two-dimensional function around an axis. The example given is a function y = √x rotated around the x-axis from x = 0 to x = 1, resulting in a solid whose volume is to be calculated. The importance of understanding the volume formula V = ∫[a to b] A(x) dx is emphasized, where A(x) represents the area of the cross-section. The paragraph concludes with the calculation of the volume of the solid formed by the given function, using the formula for the area of a circle and integrating with respect to x.

05:00

🔍 Volume Calculation for a Solid Between Two Functions

The second paragraph delves into calculating the volume of a solid formed by rotating the area between two functions, y = x (pink function) and y = x^2 (blue function), around the x-axis. The process involves understanding the geometry of the solid and breaking it down into manageable steps. The volume of the solid is found by integrating the difference in volumes of the outer and inner functions, using the formula for the area of a circle and the specific function values to determine the radius of the cross-sections. The final step involves evaluating the integral and simplifying the expression to find the volume.

10:02

📐 Complex Solids of Revolution Around a Horizontal Line

This paragraph discusses the process of finding the volume of a complex solid of revolution, which is created by rotating the area between y = x and y = x^2 around the line y = 2. The solid's volume is determined by calculating the volume of the outer function and subtracting the volume of the inner function. The explanation includes finding the radius of the circular cross-sections in terms of x and then rewriting them in terms of y for integration. The integral is then simplified by combining the two volumes into one and solving for the antiderivative, leading to the final volume calculation.

15:05

📘 Volume of Solids Rotated Around the Y-Axis

The focus shifts to solids of revolution around the y-axis, with an example of rotating the area bounded by y = x^3 and y = a (where a is a constant) around the y-axis. The process requires rewriting the area formula in terms of y, since the cross-sections are circles with radii determined by the functions' geometry. The integral is set up to calculate the volume by integrating the area formula from the lower to the upper limit of the rotation. The paragraph concludes with the evaluation of the integral to find the volume of the solid.

20:06

🌀 Solids of Revolution with Variable Cross-Sections

This paragraph explores the concept of solids of revolution with variable cross-sections, specifically focusing on the rotation around a vertical line to the left of the y-axis. The example involves rotating the area between y = x and y = x^2 around the line x = -1. The volume calculation requires understanding the geometry of the cross-sections and setting up the integral to calculate the volume of the solid. The process includes finding the radius of the cross-sections in terms of y, integrating the area formula, and simplifying the resulting expression to find the final volume.

25:09

📊 Volume Calculation for Rotated Solids with Multiple Cross-Sections

The paragraph discusses the calculation of the volume of a solid obtained by rotating the area between two functions, y = x^(1/3) and y = x^2, around the line x = 2. The process involves finding the area of the circular cross-sections for both the outer and inner functions and setting up the integral to calculate the volume. The integral is simplified by combining the two areas into one and solving for the antiderivative. The final step is to evaluate the integral within the given limits to find the volume of the solid.

30:11

📐 Detailed Steps for Volume Calculation of Complex Solids

This paragraph provides a detailed walkthrough of calculating the volume of a complex solid of revolution formed by rotating the area between y = x^(1/3) and y = x around the y-axis. The explanation includes rewriting the area formula in terms of y, setting up the integral for the volume, and simplifying the expression by combining terms and factoring out constants. The integral is then solved for the antiderivative, and the final volume is obtained by evaluating the expression at the given limits.

35:14

📘 Final Calculations for Solids of Revolution

The final paragraph wraps up the discussion on solids of revolution by presenting the calculation of the volume of a solid formed by rotating the area between two functions around a vertical line to the right of the y-axis. The process involves finding the radius of the circular cross-sections, setting up the integral for the volume, and solving for the antiderivative. The paragraph concludes with the evaluation of the integral to find the final volume of the solid, which is expressed as a fraction multiplied by pi.

Mindmap

Keywords

💡Solid of Revolution

A 'Solid of Revolution' is a three-dimensional object created by rotating a two-dimensional shape, known as a 'profile', around a line called the 'axis of revolution'. In the context of the video, this concept is central as it explains how various functions, when rotated around an axis, form different solids. The script provides examples of solids formed by rotating functions like 'y = sqrt(x)' and 'y = x' around the x-axis.

💡Volume

In the script, 'Volume' refers to the amount of three-dimensional space occupied by the solids of revolution. It is a critical concept as the video's objective is to calculate the volume of these solids. The volume is determined using integral calculus, where the area of the cross-section of the solid is integrated over a given interval.

💡Integral

An 'Integral' in calculus is a mathematical concept that represents the area under a curve, which in the video is used to find the volume of the solids. The script describes the process of integrating the area of the cross-section of the solid over a specific range to calculate its volume, as seen in the formula 'V = integral from A to B of a(x) dx'.

💡Cross-section

A 'Cross-section' in the context of the video is the two-dimensional slice of the three-dimensional solid obtained when the solid is cut by a plane. The script mentions that the cross-sections of the solids of revolution are often circular and their areas are essential for calculating the volume of the solid.

💡Radius

The 'Radius' is a term used to describe the distance from the center of a circle to its edge. In the script, the radius is used to calculate the area of the circular cross-sections of the solids. The formula for the area of a circle, πr^2, is applied in various examples, with the radius being expressed in terms of the variable 'x' or 'y' depending on the orientation of the rotation.

💡Axis

An 'Axis' in the script refers to the line around which the two-dimensional profile is rotated to create a solid of revolution. The video discusses rotation around both the x-axis and y-axis, demonstrating how the orientation of the axis affects the shape and volume of the resulting solid.

💡Function

A 'Function' in mathematics is a relation between a set of inputs and outputs. In the video, functions like 'y = sqrt(x)' and 'y = x^2' are used to define the profiles that are rotated to form solids. The script explains how the shape of these functions determines the volume of the solids when rotated around an axis.

💡Antiderivative

An 'Antiderivative' is a concept in calculus that represents a function whose derivative is another given function. In the script, antiderivatives are used to evaluate the integrals that calculate the volume of the solids. The process of finding antiderivatives is crucial for determining the areas under the curves that define the cross-sections of the solids.

💡Boundary

A 'Boundary' in the context of integration refers to the limits of integration, which define the interval over which the integral is evaluated. The script mentions boundaries in the form of 'from 0 to 1' or 'from A to B', which are the limits between which the volume of the solid is calculated.

💡Rotation

In the script, 'Rotation' refers to the process of turning a two-dimensional shape around an axis to create a three-dimensional solid. This concept is fundamental to the theme of the video, as it explains how different mathematical functions, when rotated, result in various solid shapes with calculable volumes.

Highlights

Solids of Revolution are created by rotating a 2D function around an axis to form a 3D object.

The volume of a solid of revolution can be found by integrating the area of the cross-section created by the rotation.

The formula for the volume is V = ∫[a to b] π * (radius)^2 dx or dy, depending on the axis of rotation.

For the function y = √x rotated around the x-axis from x=0 to x=1, the volume is calculated using the area formula π * x.

The volume of the solid formed by the function y = x rotated around the x-axis is found by subtracting the volume of the inner function y = x^2.

The volume of a solid with a complex shape can be determined by subtracting the volume of simpler solids within it.

For solids rotated around the y-axis, the volume formula is V = ∫[a to b] π * (radius)^2 dy.

The radius for solids rotated around the y-axis is found by expressing x in terms of y and calculating the distance from the axis.

The volume of a solid formed by rotating between two functions is the difference between the volumes of the outer and inner functions.

Integration boundaries must be carefully applied when calculating volumes to ensure accuracy.

The antiderivative is used to evaluate the integral and find the volume of the solid.

Constants such as π can be factored out of the integral to simplify calculations.

The volume of a solid obtained by rotating a function around a vertical line to the left of the y-axis is calculated similarly.

The radius for solids rotated around a vertical line is the horizontal distance from the line to the function.

Solids rotated around vertical lines to the right of the y-axis require a similar approach to find the volume.

The final volume calculation often involves simplifying complex expressions and solving for the antiderivative.

Each solid of revolution problem requires careful consideration of the function, axis of rotation, and integration limits.

Transcripts

Browse More Related Video

Calculus 1 Lecture 5.2: Volume of Solids By Disks and Washers Method

Calculating the Volume of a Solid of Revolution by Integration

Calculating volume by known cross sections

AP Calculus AB: Lesson 7.4: Disk and Washer Method

Volumes with Disks

Volume of Solids with Known Cross Sections

Related Tags

Solids of Revolution Mathematics 3D Objects Volume Calculation Integral Calculus Geometry Educational Content Problem Solving Math Tutorial Volume Formulas