Undetermined Coefficients: Solving non-homogeneous ODEs

Dr. Trefor Bazett

19 Apr 202112:43

EducationalLearning

32 Likes 10 Comments

TLDRThis video tutorial introduces the method of undetermined coefficients for solving second-order non-homogeneous differential equations with constant coefficients. The instructor explains the process of finding a particular solution by making an educated guess that mirrors the form of the non-homogeneous term, then solving for the undetermined coefficients. The video also covers how to combine the particular solution with the general solution of the homogeneous equation to obtain the complete solution. Examples are provided to illustrate the method, including handling cases where the non-homogeneous term involves exponentials, polynomials, and trigonometric functions.

Takeaways

📚 The video discusses the method of undetermined coefficients for solving second-order non-homogeneous differential equations with constant coefficients.
🔍 The method is applied when the right-hand side of the equation is not zero and is some function of the independent variable, unlike the homogeneous case.
📉 The script introduces terminology: 'y_p' for a particular solution and 'y_h' for the general solution to the homogeneous equation.
🔑 The key idea is that the sum of the homogeneous solution and any particular solution is still a solution to the non-homogeneous equation.
🤔 The difference between two particular solutions is a solution to the homogeneous equation, highlighting the flexibility in choosing a particular solution.
📝 The process involves three steps: solving the homogeneous equation, guessing a particular solution, and combining them to form the general solution.
📈 For non-homogeneous parts like exponential functions, the guess for the particular solution should mirror the form but with an undetermined coefficient.
📊 When encountering sine or cosine terms, the guess should include both sine and cosine with the same frequency, even if only one appears in the non-homogeneity.
📚 For polynomial non-homogeneities, the guess should be a polynomial of the same degree, but for repeated roots or matching solutions, multiply by 't' to the necessary power.
🔄 The method can be extended to handle combinations of different types of non-homogeneities by adding or multiplying the respective guesses.
📐 The video provides a chart as a guide for guessing the form of the particular solution based on the type of non-homogeneity present in the equation.

Q & A

What is the method of undetermined coefficients?
-The method of undetermined coefficients is a technique used to find particular solutions to non-homogeneous differential equations, where the right-hand side is a function of the independent variable.
What are constant coefficient differential equations?
-Constant coefficient differential equations are those where the coefficients of the terms involving the dependent variable and its derivatives are constants.
How does the method of undetermined coefficients handle non-homogeneous equations?
-It involves finding the general solution to the homogeneous equation and then adding a particular solution to the non-homogeneous equation.
What is the difference between a homogeneous and a non-homogeneous differential equation?
-A homogeneous differential equation has a right-hand side equal to zero, while a non-homogeneous differential equation has a right-hand side that is some function of the independent variable.
What does the term 'particular solution' mean in the context of differential equations?
-A particular solution is any specific solution to a non-homogeneous differential equation that satisfies the equation.
What is the general solution of a differential equation?
-The general solution of a differential equation includes the homogeneous solution with arbitrary constants and a particular solution.
How do you determine a particular solution using the method of undetermined coefficients?
-You guess a solution with undetermined coefficients that matches the form of the non-homogeneous term, then substitute it into the differential equation to solve for the coefficients.
Why is it important to distinguish between the homogeneous and particular solutions?
-It's important because the general solution of a non-homogeneous equation is the sum of the general solution of the homogeneous equation and a particular solution.
What is a characteristic equation in the context of differential equations?
-The characteristic equation is an algebraic equation obtained from a differential equation by assuming a solution of the form e^rt, which helps find the roots that determine the homogeneous solution.
What should you do if your guessed particular solution matches the homogeneous solution?
-If the guessed particular solution matches the homogeneous solution, you need to multiply the guess by t (or higher powers of t if necessary) to find a valid particular solution.

Outlines

00:00

📚 Introduction to Undetermined Coefficients Method

This paragraph introduces the method of undetermined coefficients for solving second-order differential equations with non-homogeneous terms. The speaker explains that while constant coefficient differential equations have been discussed, this video will focus on handling non-zero right-hand sides. The concept of a particular solution (y_p) is introduced as a specific solution to the non-homogeneous part, contrasting it with the general solution to the homogeneous part (y_h). The speaker demonstrates how to combine these solutions to solve the non-homogeneous equation, emphasizing that the sum of a homogeneous and particular solution still satisfies the original equation. The process involves plugging in the sum of solutions into the equation and showing that it simplifies to the non-homogeneous term, thus confirming the solution's validity.

05:01

🔍 Detailed Explanation of the Method with Examples

The paragraph delves into the methodology of the undetermined coefficients method with step-by-step examples. It starts by solving the homogeneous part of the equation, which is well-understood from previous studies. The speaker then moves on to finding a particular solution for the non-homogeneous part by making an educated guess that mirrors the form of the non-homogeneous term but with an undetermined coefficient. The process involves substituting the guessed solution into the equation and solving for the coefficient. The paragraph provides two examples, one with an exponential non-homogeneous term and another with a combination of an exponential and a cosine function, illustrating how to adjust the guess to avoid matching the homogeneous solution. The speaker also discusses the importance of the order in which solutions are combined and the absence of constants in the particular solution.

10:02

📘 General Guidelines for Guessing Particular Solutions

The final paragraph summarizes the general rules for guessing particular solutions based on the type of non-homogeneity present in the differential equation. The speaker outlines a chart that categorizes different types of non-homogeneous terms, such as exponentials, polynomials, sine and cosine terms, and provides corresponding guesses for the particular solution. For instance, an exponential non-homogeneity would prompt a guess of an exponential form with an undetermined coefficient. For sine and cosine terms, both functions must be included in the guess, even if only one appears in the non-homogeneous term. Polynomials require a guess that is one degree higher than the non-homogeneity. The speaker also notes the need to multiply guesses by powers of the independent variable to avoid matching the homogeneous solution and concludes with a complex example involving a polynomial, an exponential, and a cosine function, demonstrating how to combine these rules for a comprehensive guess.

Mindmap

Keywords

💡Undetermined Coefficients

The method of undetermined coefficients is a technique used to find particular solutions to non-homogeneous differential equations. It involves guessing a solution that has the same form as the non-homogeneous part of the equation but with undetermined coefficients. In the video, this method is introduced to solve second-order differential equations when the right-hand side is not zero, as opposed to homogeneous equations where the right-hand side is zero.

💡Second-Order Differential Equations

A second-order differential equation is an equation that involves the second derivative of a function. In the context of the video, the focus is on solving such equations with non-constant right-hand sides, which are not zero, unlike the previously discussed homogeneous equations. The video script provides a detailed approach to finding solutions to these equations using the method of undetermined coefficients.

💡Constant Coefficients

Constant coefficients refer to the coefficients in front of the terms of a differential equation that do not change. In the video, the speaker mentions that the left side of the differential equations discussed has only constant coefficients in front of the various terms y, y prime, and y double prime, which simplifies the process of finding solutions.

💡Homogeneous Equations

A homogeneous differential equation is one where the right-hand side is zero. The video script explains that the method of undetermined coefficients is particularly useful when dealing with non-homogeneous equations, but it contrasts this with the previously studied homogeneous equations, which are simpler to solve because they only involve the left-hand side of the equation.

💡Particular Solution

A particular solution, denoted as y_sub_p in the script, is a specific solution to a non-homogeneous differential equation. It is not the general solution but one that satisfies the non-homogeneous part of the equation. The video describes how to find a particular solution by making an educated guess that mirrors the form of the non-homogeneous term.

💡General Solution

The general solution, denoted as y_sub_h in the script, includes all possible solutions to a homogeneous differential equation, typically involving constants. The video explains that the general solution to a non-homogeneous equation is the sum of the general solution to the homogeneous part and any particular solution to the non-homogeneous part.

💡Characteristic Equation

The characteristic equation is derived from a homogeneous differential equation by assuming a solution of the form e to the rt. In the video, the characteristic equation is used to find the roots, which then help in writing the general solution to the homogeneous system of the differential equation.

💡Non-Homogeneous

Non-homogeneous refers to a differential equation where the right-hand side is not zero, indicating the presence of a non-zero function or term. The video discusses methods for finding solutions to non-homogeneous equations, which include guessing a particular solution that matches the form of the non-homogeneous term.

💡Product Rule

The product rule is a fundamental calculus rule used to differentiate the product of two functions. In the context of the video, the product rule is applied when differentiating the guessed particular solution, which often involves terms multiplied together, such as in the case of a times te to the minus t.

💡Polynomial

A polynomial is an algebraic expression consisting of variables and coefficients, involving only addition, subtraction, multiplication, and non-negative integer exponents of variables. In the video, when the non-homogeneous part of the differential equation is a polynomial, the method of undetermined coefficients involves guessing a polynomial of the same degree for the particular solution.

💡Exponential

An exponential function is a mathematical function of the form e to the rt, where e is the base of the natural logarithm, and r and t are variables. The video script mentions that when the non-homogeneous term is an exponential, the particular solution should be guessed as an exponential with an undetermined coefficient.

💡Sine and Cosine Terms

Sine and cosine are trigonometric functions that are often part of the non-homogeneous terms in differential equations. The video explains that if the non-homogeneous part includes sine or cosine, the particular solution should include both sine and cosine terms with undetermined coefficients, even if only one is present in the non-homogeneous term.

Highlights

Introduction to the method of undetermined coefficients for solving non-homogeneous second order differential equations.

Explanation of constant coefficient differential equations and the transition to non-zero right-hand side functions.

Terminology clarification: 'particular solution' (y_sub_p) and 'homogeneous solution' (y_sub_h).

The concept that the sum of a homogeneous and particular solution solves the non-homogeneous equation.

Demonstration of how the difference between two particular solutions is a homogeneous solution.

Methodology to find the general solution by combining the homogeneous and any particular solution.

Step-by-step guide to solving the homogeneous part of the equation using characteristic equations.

The process of guessing a particular solution that mirrors the form of the non-homogeneous term.

Use of undetermined coefficients 'a' in guessing the particular solution structure.

How to derive the particular solution by plugging in the guessed form and solving for the coefficients.

Combining the homogeneous and particular solutions to form the general solution.

The importance of forming the general solution by adding the homogeneous and particular solutions in the correct order.

Illustration of a second example with a different non-homogeneous term, 3e to the minus t.

The necessity to adjust the guess for the particular solution when it overlaps with the homogeneous solution.

Technique of multiplying the guess by 't' to avoid overlap with the homogeneous solution.

General guidelines for guessing particular solutions based on the form of the non-homogeneous term.

Chart provided for different types of non-homogeneities and the corresponding guesses for particular solutions.

Handling of complex non-homogeneous terms by combining appropriate guesses for each component.

Final example demonstrating a messy non-homogeneous term with a combination of polynomial, exponential, and trigonometric components.

Conclusion emphasizing the algebraic process of solving for multiple coefficients in complex cases.

Transcripts

Browse More Related Video

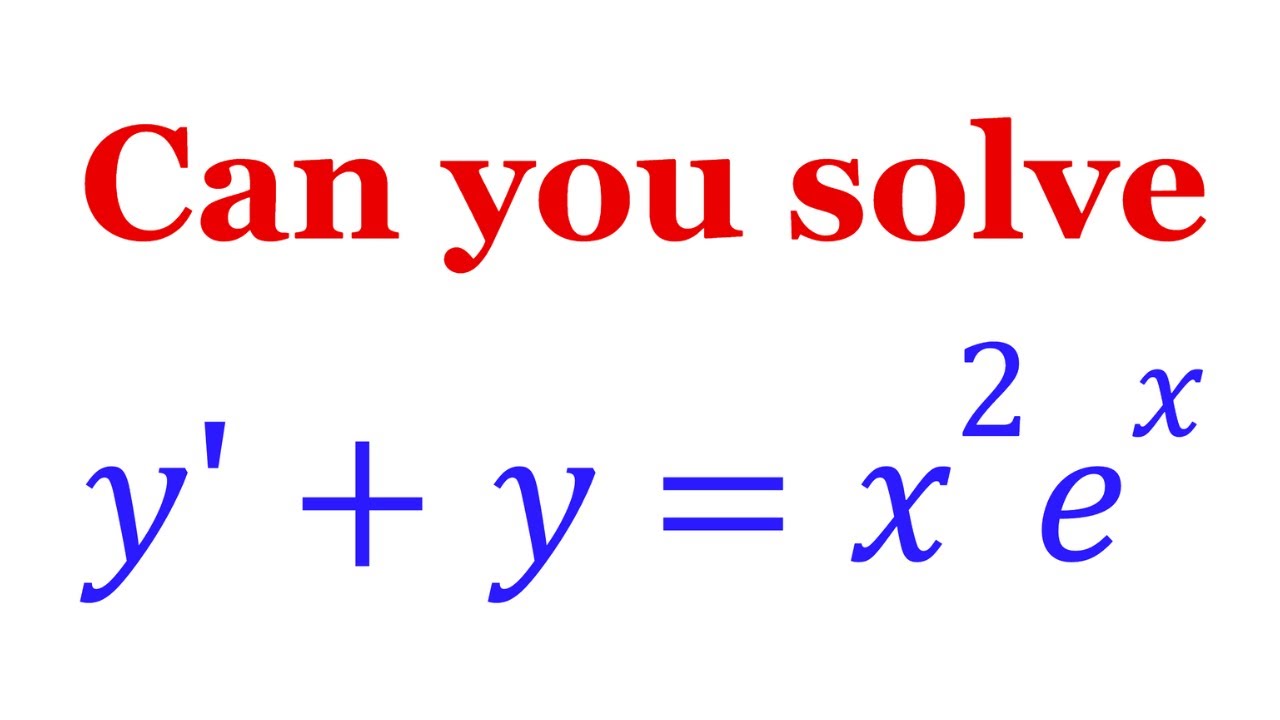
Let's Solve An Interesting Differential Equation

The Theory of Higher Order Differential Equations

Homogeneous Differential Equations

How to Solve Constant Coefficient Homogeneous Differential Equations

The Theory of 2nd Order ODEs // Existence & Uniqueness, Superposition, & Linear Independence

First order, Ordinary Differential Equations.