The Theory of Higher Order Differential Equations
TLDRThis video script delves into the theory of higher order linear differential equations, exemplified by a fourth derivative equation. It establishes a theoretical foundation for solving such equations, emphasizing the general form of an nth order linear differential equation with coefficient functions and a non-homogeneous term. The video introduces the existence and uniqueness theorem, the principle of superposition, and the general solution theorem, highlighting the significance of finding n linearly independent solutions and the role of the Wronskian in determining the general solution. It also draws parallels with linear algebra concepts, equating a fundamental set of solutions to a basis in n-dimensional space.
Takeaways
- 📚 The video introduces the theory of higher order linear differential equations, focusing on equations with derivatives up to the nth order.
- 🔍 It aims to provide a solid theoretical foundation for solving these types of equations, emphasizing the importance of understanding the underlying theory.
- 📈 The general form of a linear higher order differential equation is presented, highlighting the role of coefficient functions and the dependent variable y.
- 🏷️ The concept of 'homogeneous' equations is introduced, where the right-hand side of the equation is zero, which simplifies the analysis.
- 🔑 The existence and uniqueness theorem is discussed, which guarantees that under certain conditions, there exists a unique solution to the differential equation.
- 📝 The importance of initial value problems (IVPs) is emphasized, requiring n initial conditions for an nth order equation to ensure a unique solution.
- 🌐 The principle of superposition is explained, stating that linear combinations of solutions to a homogeneous equation are also solutions, aiding in finding the general solution.
- 📉 The Wronskian is introduced as a test for determining the linear independence of solutions, which is crucial for establishing the general solution.
- 🎯 The general solution theorem is presented, which states that if n linearly independent solutions are found, they form a fundamental set that describes every possible solution to the equation.
- 🔄 The process of solving nth order differential equations is outlined: find n solutions, check for linear independence using the Wronskian, and then express the general solution as a linear combination of these solutions.
- 🔄 The video connects the theory to previously discussed methods, such as solving constant coefficient ODEs, showing the compatibility and applicability of the general theory.
Q & A
What is the main topic of the video?
-The main topic of the video is the theory of higher order linear differential equations, focusing on their solutions and the foundational concepts required to understand and solve these equations.
What is a higher order linear differential equation?
-A higher order linear differential equation is an equation that involves the dependent variable y and its derivatives up to the nth order, with each term being a linear combination of the derivatives multiplied by a coefficient function.
What is the significance of the term 'homogeneous' in the context of differential equations?
-In the context of differential equations, 'homogeneous' refers to an equation where the right-hand side is equal to zero, which simplifies the process of finding solutions.
What is an Initial Value Problem (IVP) in the context of differential equations?
-An Initial Value Problem (IVP) consists of a differential equation and a set of initial conditions that specify the values of the dependent variable and its derivatives at a certain point in the domain.
What is the Existence and Uniqueness Theorem mentioned in the video?
-The Existence and Uniqueness Theorem states that for a given nth order linear differential equation with continuous coefficient functions and an initial value problem, there exists a unique solution on the interval where the coefficients and the function on the right-hand side are continuous.
What is the Principle of Superposition in the context of differential equations?
-The Principle of Superposition states that if you have n solutions to an nth order homogeneous differential equation, any linear combination of these solutions also solves the differential equation, due to the linearity of the equation and its derivatives.
What is the Wronskian and how is it used in determining the general solution of a differential equation?
-The Wronskian is a determinant used to test the linear independence of a set of solutions to a differential equation. If the Wronskian of n solutions is nonzero at some point, it indicates that these solutions are linearly independent and form a fundamental set, meaning any solution to the equation can be written as a linear combination of these solutions.
What is the connection between the Wronskian and the linear independence of solutions?
-The Wronskian serves as a test for linear independence. If the Wronskian of a set of solutions is nonzero at some point, it confirms that the solutions are linearly independent, which is a requirement for them to form a fundamental set that can represent the general solution of the differential equation.
What is the method for solving an nth order linear differential equation as described in the video?
-The method involves finding n solutions to the nth order differential equation, checking their linear independence using the Wronskian, and if they are linearly independent, then any solution to the equation can be expressed as a linear combination of these n solutions, which is the general solution.
How does the theory of higher order linear differential equations relate to the previously discussed theory of second order differential equations?
-The theory of higher order linear differential equations parallels the theory of second order differential equations in many ways, such as the Existence and Uniqueness Theorem and the Principle of Superposition, but with the extension to n initial conditions and the nth order of the differential equation.
Outlines
📚 Introduction to Higher Order Linear Differential Equations
The speaker begins by introducing the concept of higher order linear differential equations, exemplified by a fourth derivative equation with coefficients and a function of x. The goal is to establish a theoretical foundation for solving such equations. The general form of these equations is described, involving dependent variables and their derivatives up to the nth order, with coefficient functions and a possible non-zero function f(x) on the right-hand side. The video aims to explore the theory behind nth order homogeneous and non-homogeneous linear differential equations, with a link to a previous video on second order equations provided for context. The first theorem discussed is the existence and uniqueness theorem, which guarantees a single solution to an initial value problem (IVP) with n initial conditions, assuming continuity of the coefficient functions and f(x) over an interval.
🔍 The Principle of Superposition and General Solution Theorem
The speaker continues by explaining the principle of superposition, which states that if you have n solutions to an nth order homogeneous differential equation, any linear combination of these solutions also solves the equation. This principle is powerful as it allows for the rapid expansion of solutions. The speaker then introduces the general solution theorem, which posits that n solutions to an nth order linear differential equation can describe every possible solution, provided the Wronskian of these solutions is non-zero at some point. This theorem helps determine when to stop searching for new solutions, as n linearly independent solutions form a fundamental set, allowing any solution to be expressed as a linear combination of them. The analogy to linear algebra is made, where n linearly independent vectors form a basis in n-dimensional space. The method for solving nth order differential equations involves finding n solutions, checking for linear independence via the Wronskian, and then formulating the general solution as linear combinations of these solutions. The speaker reviews previous methods for solving constant coefficient ODEs, showing their compatibility with the current theory.
Mindmap
Keywords
💡Higher Order Linear Differential Equations
💡Coefficient Function
💡Homogeneous
💡Initial Value Problem (IVP)
💡Existence and Uniqueness Theorem
💡Principle of Superposition
💡General Solution
💡Wronskian
💡Fundamental Set
💡Characteristic Equation
Highlights
Introduction of the theory of higher order linear differential equations.
Equation example with the fourth derivative and coefficient function x squared.
Goal to lay a solid theoretical foundation for solving these differential equations.
General form of a linear higher order differential equation with dependent variable y and its nth order derivative.
Assumption of linearity and coefficient functions labeling for each derivative.
Homogeneous equation concept when f(x) is zero.
Link to the second order theory video for further understanding.
Existence and uniqueness theorem for initial value problems in differential equations.
Requirement of n initial conditions for an nth order differential equation.
Condition for the existence and uniqueness of solutions based on continuity of functions.
Principle of superposition for homogeneous differential equations.
Finding n solutions and forming infinite families through linear combinations.
General solution theorem for nth order linear differential equations.
Wronskian test for determining linear independence of solutions.
Concept of a fundamental set of solutions as a basis in n-dimensional space.
Method to solve nth order differential equations by finding n linearly independent solutions.
Review of constant coefficient ODEs and their compatibility with the general theory.
Different scenarios for finding solutions, including repeated and complex roots.
Generalization of methods for higher dimensions in solving differential equations.
Conclusion emphasizing the compatibility of the theory with previously introduced methods.
Transcripts
Browse More Related Video

The Theory of 2nd Order ODEs // Existence & Uniqueness, Superposition, & Linear Independence

Linear Differential Equations & the Method of Integrating Factors

How to Solve Constant Coefficient Homogeneous Differential Equations

Lec 1 | MIT 18.03 Differential Equations, Spring 2006
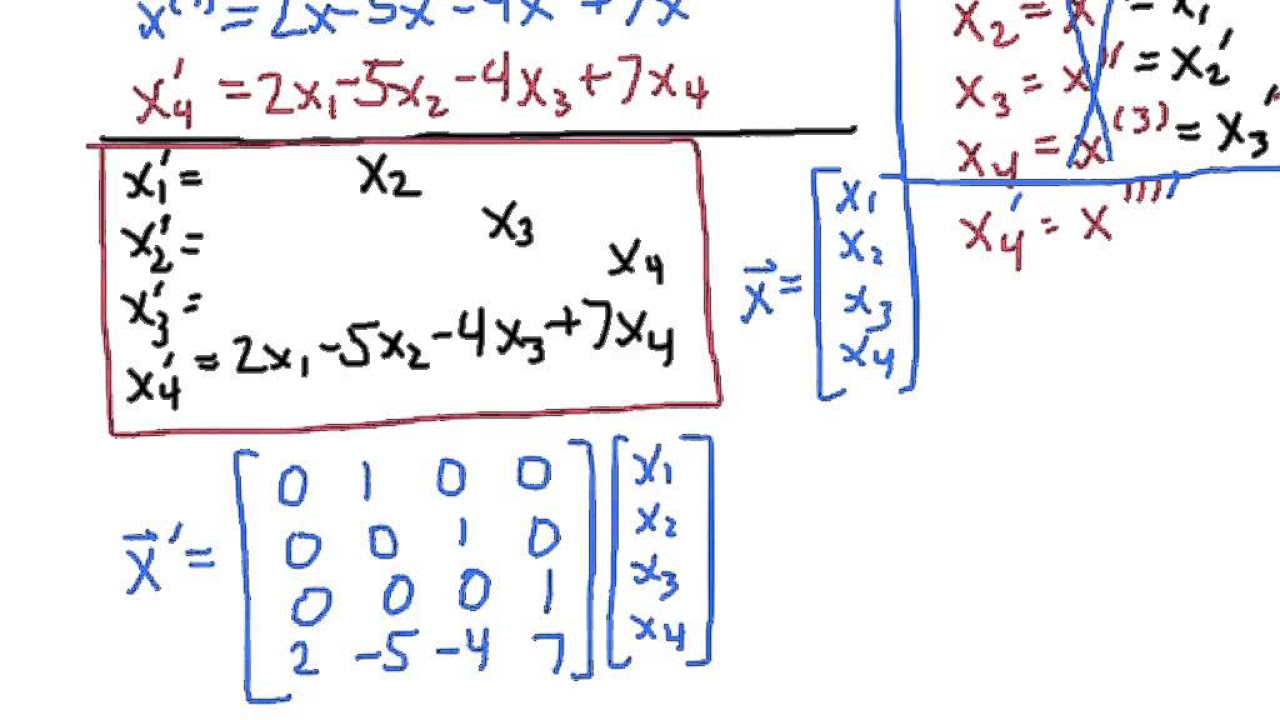
Converting a Higher Order ODE Into a System of First Order ODEs

Undetermined Coefficients: Solving non-homogeneous ODEs
5.0 / 5 (0 votes)
Thanks for rating: