Analysis III - Integration: Oxford Mathematics 1st Year Student Lecture

Oxford Mathematics

9 May 201954:28

EducationalLearning

32 Likes 10 Comments

TLDRThis video script introduces 'Analysis 3', a course focused on rigorously defining the concept of an integral. It covers the Riemann integral's intuitive approach and its limitations, including the inability to integrate certain functions. The lecturer opts for the Darboux integral for its intuitive development, which equates to the Riemann integral under proof. The script delves into the fundamentals, including step functions, partitions, and the integral's definition through upper and lower sums. The course aims to establish a comprehensive understanding of integration, differentiating it from school-level knowledge.

Takeaways

📚 The course 'Analysis 3' focuses on making the concept of an integral rigorous, clarifying and proving fundamental facts about integration.
🔍 The course will explore the relationship between integration and differentiation, establishing them as opposite operations through careful formulation and proof.
📈 The course will define and work with basic functions, such as exponential and logarithm functions, which are often defined using integration.
📏 The concepts of circumference and area of a circle, and the constant 'pi', will be rigorously defined using integrals, showing their foundational role in geometry.
🤔 The course will introduce the Riemann integral, acknowledging its intuitive nature but also discussing its limitations, such as the inability to integrate certain functions.
📘 Professionals often use the Lebesgue integral due to its broader applicability, despite its more complex definition compared to the Riemann integral.
🎓 The course will initially discuss the Darboux integral, which is found to be equivalent to the Riemann integral, providing a more intuitive approach to developing the theory.
📝 The importance of step functions in defining the integral is highlighted, as they are the building blocks for more complex functions and integrals.
📐 The script introduces the concept of partitions and refinements of partitions, essential for understanding the structure of step functions and their integrals.
📉 The integral of a step function is defined in a way that is intuitively appealing, measuring the 'area' under the graph of the function, which is independent of the function's value at partition points.
🔢 The integral of an arbitrary function is defined by approximating it with step functions, using the supremum of lower sums and the infimum of upper sums to capture the integral's value.

Q & A

What is the primary focus of the course 'Analysis 3'?
-The primary focus of the course 'Analysis 3' is to make the notion of an integral rigorous. This involves providing a mathematically rigorous definition and understanding of integrals, which are typically introduced in a more intuitive manner in earlier education.
What is the significance of the integral of x squared from 0 to 1 being one-third?
-The significance of the integral of x squared from 0 to 1 being one-third is that it demonstrates a fundamental fact in calculus. This fact is often introduced in a non-rigorous manner, but the course aims to provide a rigorous understanding of such integrals.
Why are integration and differentiation considered opposite operations?
-Integration and differentiation are considered opposite operations because they undo each other in a certain sense. The course will formulate this relationship carefully and prove several versions of this fundamental principle in calculus.
What are some functions that are best defined using integration?
-Some functions that are best defined using integration include the exponential and logarithm functions. These functions are fundamental in mathematics and their definitions often rely on the concept of integration.
Why is the circumference of a circle related to the concept of integration?
-The circumference of a circle is related to the concept of integration because to define the circumference or the area of a shape that is not a simple rectangle, one needs to understand what an integral is. The course will explore this relationship and how integrals help in defining these geometric properties.
What is the Riemann integral and why is it not the focus of the course?
-The Riemann integral is a type of integral that is relatively intuitive and easy to define. However, it has some shortcomings, such as the inability to integrate some functions that one might want to. The course will instead focus on the Darboux integral, which is shown to be equivalent to the Riemann integral later in the course.
What is the difference between the Riemann integral and the Lebesgue integral?
-The Riemann integral is more intuitive and easier to define but has limitations in terms of the functions it can integrate. The Lebesgue integral, on the other hand, is more difficult to define but has broader applicability and is used by professionals in the field. The course will eventually show that the Darboux integral, which is similar to the Riemann integral, is equivalent to the Lebesgue integral whenever it exists.
What is a step function and why is it important in the course?
-A step function is a function that is constant on each interval defined by a sequence of points between a and b. It is important in the course because step functions are used in defining the integral. They serve as a basis for approximating more complex functions in the process of integration.
What is the definition of a partition in the context of this course?
-A partition in this context is a sequence of points that splits the interval between a and b into finitely many parts. It is fundamental in the process of defining and calculating integrals, especially in relation to step functions.
What is the significance of the indicator function in the context of step functions?
-The indicator function is a function that takes the value 1 on a set X and 0 elsewhere. It is significant in the context of step functions because step functions can be represented as linear combinations of indicator functions of intervals. This representation helps in understanding the structure and properties of step functions.
How is the integral of a step function defined in the course?
-The integral of a step function is defined by summing the product of the constant value the function takes on each interval and the length of that interval. This definition is used as a basis for approximating the integral of more complex functions.
What is the definition of integrability in the context of this course?
-A function is integrable if for any given epsilon greater than zero, one can find minor and major step functions (Phi minus and Phi plus) such that the difference between their I values is at most epsilon. This means that the integral can be approximated by step functions to any desired degree of accuracy.
What is the relationship between the integral of a function and the I values of minor and major step functions?
-The integral of a function is defined as the common value of the I values of minor and major step functions that approximate the function from below and above. If a function is integrable, then the I values of any minor and major step functions approximating the function will be arbitrarily close to each other.

Outlines

00:00

📚 Introduction to Analysis 3: Rigorizing the Integral Concept

The video script introduces the course 'Analysis 3' focusing on the concept of integration. The instructor aims to provide a rigorous foundation for the integral, explaining concepts that students may have been familiar with since school, such as the integral of x squared from 0 to 1 being one-third. The course will also explore the relationship between integration and differentiation, the definition of basic functions like exponential and logarithm through integration, and geometrical applications like the circumference and area of a circle. The instructor apologizes for not covering the 'right integral' and instead focusing on the Riemann integral due to its intuitive nature, despite its limitations.

05:06

🔍 Exploring the Darboux Integral and Its Relation to Riemann

The script discusses the shortcomings of the Riemann integral, noting that some functions cannot be integrated using it, which is why professionals prefer the Lebesgue integral. The instructor, however, chooses to teach the Darboux integral, finding it more intuitive for developing the theory. It is later proven in the course that the Darboux integral is equivalent to the Riemann integral. The instructor advises students to be cautious with other resources until they have a solid understanding of the Darboux integral.

10:11

📉 Understanding Step Functions and Their Role in Integration

The script delves into the definition of step functions, which are fundamental to the course. Step functions are real-valued functions that remain constant on open intervals between a sequence of points. The instructor provides an example of a step function and explains the concept of a partition, which is a sequence of points dividing an interval into parts. The script also introduces the idea of a refinement of a partition, which involves adding more points to an existing partition without removing any.

15:21

📝 Basic Lemmas and Properties of Step Functions

The instructor presents several basic lemmas about step functions and partitions, including that a step function adapted to a partition remains a step function if the partition is refined. It is also stated that if there are two different partitions, there exists a common refinement for both. The lemmas establish that the space of step functions is closed under basic operations such as addition, scalar multiplication, and taking the maximum or minimum of two functions.

20:29

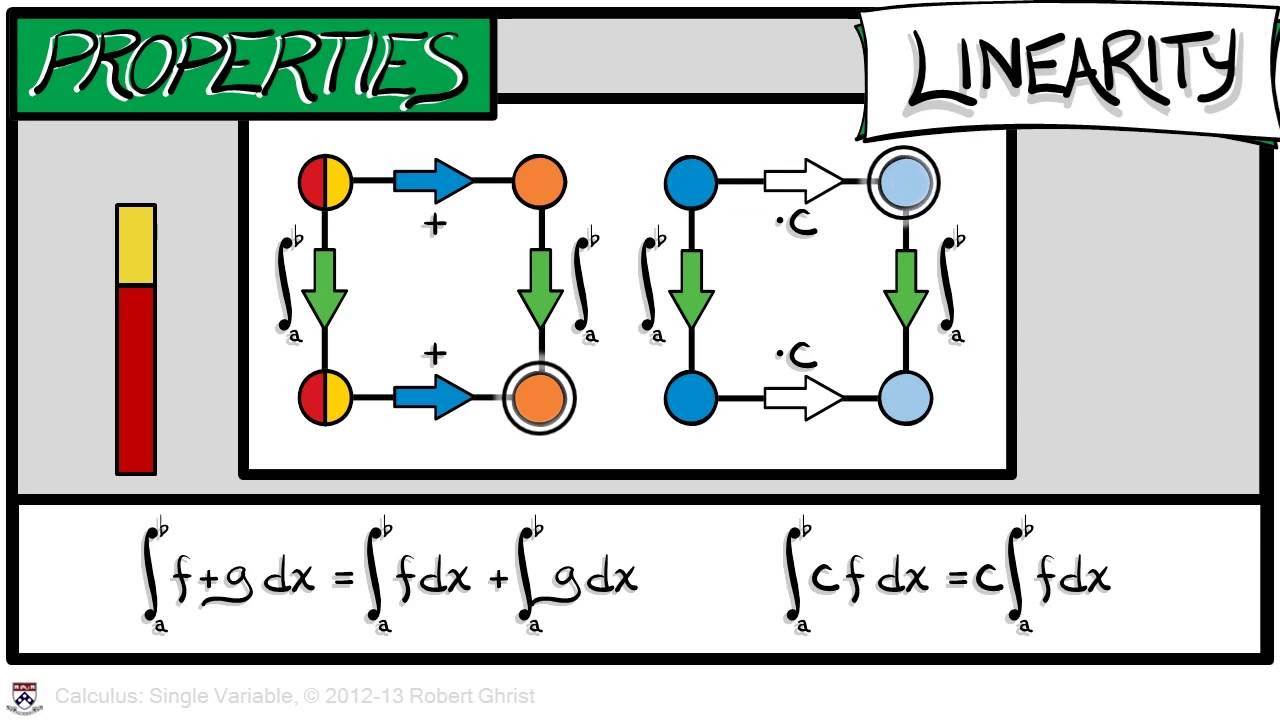
📐 The Integral of a Step Function and Its Linearity

The script defines the integral of a step function in terms of the sum of the product of the constant values the function takes on each interval of the partition and the length of those intervals. The instructor uses an example to illustrate this definition and emphasizes that the integral's value is independent of the function's values at the partition points. The section concludes by establishing that the integral is a linear functional on the space of step functions.

25:39

🌟 Defining the Integral for Arbitrary Functions

The instructor explains the process of defining the integral for arbitrary functions by 'sandwiching' them between step functions, known as minorants and majorants. A function is considered integrable if it can be bounded above by majorants and below by minorants such that the integral values of these step functions can be made arbitrarily close. The integral of the function is then defined as the common value that these step functions converge to.

30:45

📌 Conditions for Integrability and the Existence of the Integral

The script highlights the conditions under which a function is integrable, emphasizing that the integral values of minorants and majorants must be within any given epsilon of each other. This means that for any positive epsilon, there exist minorants and majorants whose integral values differ by no more than epsilon. The instructor also notes that the integral of a function is always bounded by the integral values of any minorant and majorant, providing a foundational understanding of integrability.

Mindmap

Keywords

💡Integration

Integration is a fundamental concept in calculus that represents the process of finding the accumulated quantity of a variable, often understood as the area under a curve between two points. In the context of the video, integration is being rigorously defined to move beyond intuitive understanding to a more formal mathematical concept. The script mentions making rigorous sense of integrals such as the integral of x squared from 0 to 1 being one-third.

💡Riemann Integral

The Riemann Integral is a method of defining the integral of a function, which is intuitive and relatively easy to define, as mentioned in the script. However, it has limitations and is not suitable for all functions that one might want to integrate. The video course will focus on this type of integral due to its accessibility, despite its shortcomings.

💡Darboux Integral

The Darboux Integral is an alternative approach to defining the integral of a function, which the instructor finds more intuitive for developing the theory of integration. The script explains that it will be proven later in the course that the Darboux integral is equivalent to the Riemann integral, but the Darboux method is used initially for its clarity in teaching.

💡Step Functions

Step functions are simple functions that are constant on consecutive intervals and are used as a basis for defining more complex integrals. In the script, step functions are introduced as a starting point for understanding the integral, with the integral of a step function being defined as the sum of the products of the function's values and the lengths of the intervals.

💡Partition

A partition, in the context of the video, refers to a sequence of points that splits an interval into a finite number of parts. It is used in the definition of the integral of a step function and is fundamental to the concept of refining partitions to better approximate the integral of a function.

💡Refinement

Refinement, in the context of partitions, is the process of adding more points to an existing partition, thus creating a new partition with more细分intervals. The script discusses the concept of refinement to illustrate how step functions can be adapted to different partitions and how integrals can be made more precise through finer partitions.

💡Indicator Function

The indicator function is a function that takes the value 1 for elements within a certain set and 0 elsewhere. In the script, it is used to express step functions as linear combinations of indicator functions of intervals, which is a key step in understanding the structure of step functions and their integrals.

💡Linear Functional

A linear functional is a linear map between vector spaces. In the script, the integral of a step function is described as a linear functional on the space of step functions, meaning it preserves the operations of vector addition and scalar multiplication, which is crucial for the properties of the integral.

💡Majorant and Minorant

Majorant and minorant are terms used to describe step functions that are respectively greater than or equal to, and less than or equal to, a given function at every point. In the script, these concepts are used to define the integrability of a function by sandwiching it between step functions and showing that the integral can be approximated by these step functions.

💡Supremum and Infimum

The supremum and infimum are the least upper bound and the greatest lower bound of a set of numbers, respectively. In the script, these terms are used in the definition of the integral of a function, where the integral is the common value of the supremum of the integrals of all minorants and the infimum of the integrals of all majorants of the function.

Highlights

Introduction to Analysis 3 focusing on rigorously defining the concept of an integral.

Explaining the Riemann integral's intuitive nature and its shortcomings, including inability to integrate certain functions.

Professional mathematicians prefer the Lebesgue integral for its broader applicability.

The course will use the Darboux integral, which is proven to be equivalent to the Riemann integral, offering an intuitive approach to the theory.

The importance of caution when referencing external materials due to different approaches in defining integrals.

Definition and importance of step functions in the preliminary course on integration.

Explanation of partitions and how they refine the understanding of step functions.

Lemma on the properties of step functions, including their closure under basic operations.

Introduction of indicator functions and their role in representing step functions.

The integral of a step function is defined in relation to a partition, highlighting its independence from the choice of partition.

I as a linear functional on the space of step functions, emphasizing its properties and behavior.

Defining the integral of an arbitrary function by sandwiching it between minor and major step functions.

Conditions for a function to be considered integrable, involving the closeness of I values of minor and major step functions.

The integral of a function is presented as the common value of the supremum of I over minor step functions and the infimum over major step functions.

The integral's intuitive appeal in approximating an arbitrary function by step functions from above and below.

Clarification on the existence of majorants and minorants for bounded functions, ensuring the integral's existence.

The relationship between the I values of minor and major step functions, establishing a foundational understanding of integral bounds.

Transcripts

Browse More Related Video

Calculus - Lesson 14 | Integral of a Function | Don't Memorise

Definite integral as the limit of a Riemann sum | AP Calculus AB | Khan Academy

Calculus Chapter 3 Lecture 25 Definite Integrals

"Reverse" Riemann Sums | Finding the Definite Integral Given a Sum

Riemann sum | MIT 18.01SC Single Variable Calculus, Fall 2010

BusCalc 13.4 Riemann Sums

Related Tags

Calculus Integration Riemann Integral Darboux Integral Step Functions Vector Space Indicator Functions Math Theory Educational Content Advanced Math