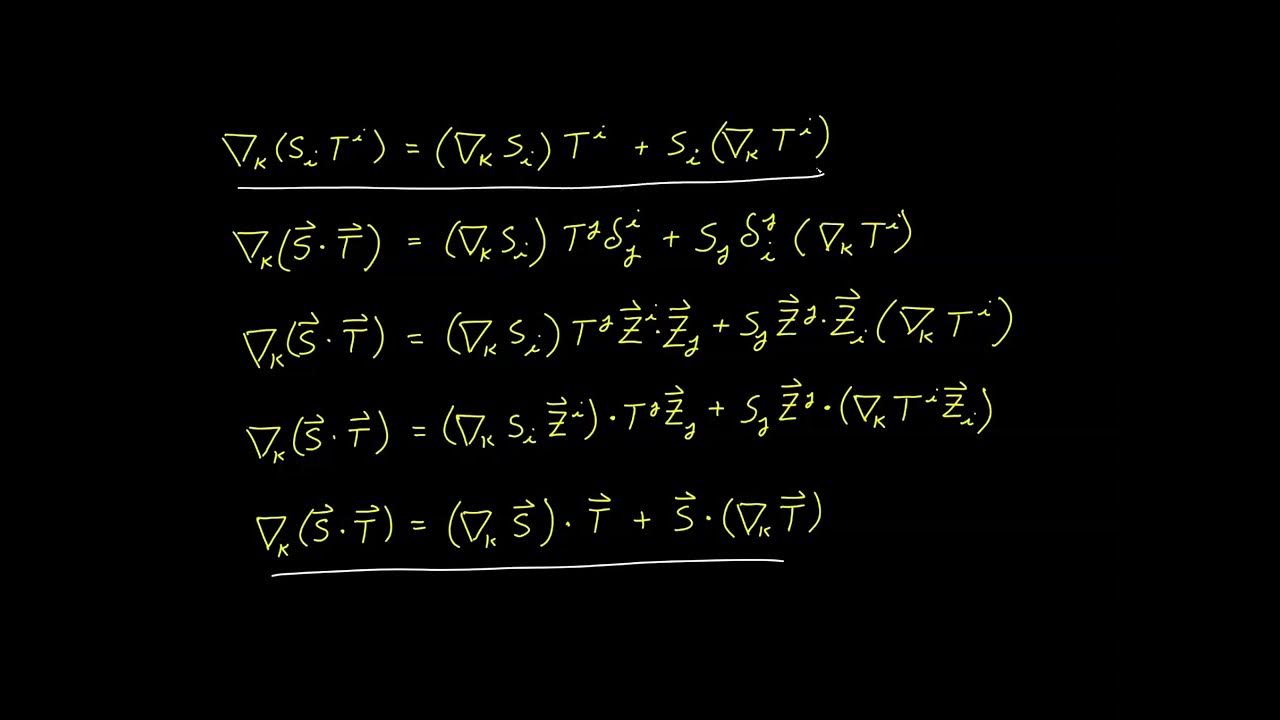Video 14 - Dot Product
TLDRThis video, the 14th in a series on tensor calculus, delves into the dot product, a fundamental vector operation essential for advanced topics. The script introduces a novel definition of the dot product in tensor calculus, distinct from the Cartesian coordinate system's traditional formula. It demonstrates deriving key properties, including the scalar nature of the dot product, its commutative and distributive properties, and its relationship with vector magnitudes and angles. The video also covers the dot product in Cartesian coordinates and concludes with the derivative of the dot product, paralleling the product rule in calculus.
Takeaways
- 📚 The video introduces the concept of the dot product in the context of tensor calculus, emphasizing its importance for understanding future topics.
- 🔍 The traditional definition of the dot product in linear algebra is deemed insufficient for tensor calculus due to its dependency on the Cartesian coordinate system.
- 📐 An alternate definition of the dot product is presented, which does not assume prior knowledge of angles and is more suitable for tensor calculus.
- 📉 The video demonstrates the derivation of the dot product's properties, including its scalar result, using the law of cosines and vector manipulation.
- 🔄 The commutative property of the dot product is highlighted, showing that the order of vectors does not affect the outcome of the operation.
- 📏 The script explains how the dot product can be used to define the length of a vector by taking the dot product of the vector with itself.
- 📈 The video derives a generalized formula for the angle between vectors in any dimension using the dot product.
- ⚖️ The distributive property of the dot product over vector addition is proven algebraically, showing that it holds true in any coordinate system and dimension.
- 📝 The script provides a proof for the dot product in Cartesian coordinates, illustrating how it simplifies to the sum of the products of corresponding components.
- 🔢 The derivative of the dot product with respect to time is derived, showing that it follows a pattern similar to the product rule for ordinary functions.
- 📘 The video concludes with a summary of the key properties and definitions of the dot product, preparing viewers for the introduction of the covariant metric tensor in the next video.
Q & A
What is the dot product and why is it important in tensor calculus?
-The dot product is a fundamental vector operation that is crucial for understanding many concepts in tensor calculus. It is a way to combine the magnitudes of two vectors and the cosine of the angle between them to produce a scalar value.
Why is the traditional definition of the dot product not suitable for tensor calculus?
-The traditional definition of the dot product is only valid in the Cartesian coordinate system, which makes it unsuitable for tensor calculus that requires a more generalized approach applicable to any coordinate system.
What is the alternate definition of the dot product used in tensor calculus?
-In tensor calculus, the dot product is defined in a way that does not rely on the Cartesian coordinate system. It is defined in terms of the magnitudes of the vectors and the cosine of the angle between them, allowing for a more generalized approach.
How does the law of cosines relate to the dot product in the context of tensor calculus?
-The law of cosines is used to derive the magnitude of a vector resulting from the subtraction of two vectors. This process leads to an expression that, when simplified, results in the alternate definition of the dot product used in tensor calculus.
What is the significance of deriving the dot product from the tensor calculus definition?
-Deriving the dot product from the tensor calculus definition allows us to establish the necessary properties of the dot product, including its scalar nature, commutative property, and its relationship with the angle between vectors.
How can the dot product be used to define the length of a vector?
-The length of a vector can be defined by taking the dot product of the vector with itself. This results in a scalar value that represents the square of the vector's magnitude.
What is the commutative property of the dot product and why is it important?
-The commutative property of the dot product states that the order of the vectors does not affect the result of the dot product. This property is important because it allows for flexibility in calculations and confirms that the dot product is symmetric with respect to the vectors involved.
How does the dot product help in defining a generalized angle in any dimension?
-The dot product can be inverted to express the angle between two vectors in terms of their dot product. This provides a formula for calculating the angle in any dimensional space using only the dot product and the magnitudes of the vectors.
What is the distributive property of the dot product and how is it proven?
-The distributive property of the dot product states that the dot product is distributive over vector addition, meaning a dot (b + c) equals a dot b plus a dot c. This property is proven using algebraic manipulation and the properties of the dot product already established.
How is the dot product expressed in Cartesian coordinates?
-In Cartesian coordinates, the dot product of two vectors is expressed as the sum of the products of their corresponding components, taking advantage of the orthogonality of the basis vectors and the distributive property of the dot product.
What is the derivative of the dot product of two vectors and how is it derived?
-The derivative of the dot product of two vectors with respect to a parameter is derived using the definition of the derivative and the distributive property of the dot product. It results in a formula that is similar to the product rule for ordinary functions, involving the derivatives of the vectors with respect to the parameter.
How will the understanding of the dot product be used in future topics of tensor calculus?
-The understanding of the dot product is foundational for defining more complex tensor operations and for analyzing the geometric and physical properties of spaces in tensor calculus, including the introduction of the covariant metric tensor in subsequent topics.
Outlines
📚 Introduction to Tensor Calculus and Dot Product
This paragraph introduces the topic of the video, which is the dot product within the context of tensor calculus. It emphasizes the importance of the dot product as a foundational vector operation for further studies in tensor calculus. The traditional definition of the dot product from linear algebra is mentioned, along with its limitations in non-Cartesian coordinate systems. The video promises to present an alternative definition of the dot product suitable for tensor calculus, which will be used to derive its properties, including the familiar algebraic expression involving magnitudes and the cosine of the angle between two vectors.
🔍 Deriving the Dot Product Using Tensor Calculus
The paragraph delves into the process of deriving the dot product in tensor calculus. It starts by defining the dot product in a novel way and then uses geometric constructions and the law of cosines to derive the traditional algebraic expression for the dot product. The process involves creating new vectors, applying the law of cosines to find magnitudes, and manipulating these to eventually show that the dot product is equivalent to the product of the magnitudes of the vectors and the cosine of the angle between them. The paragraph also introduces a 'fact sheet' to keep track of the properties of the dot product as they are discovered.
📘 Properties of the Dot Product in Tensor Calculus
This section explores the properties of the dot product as derived from the tensor calculus definition. It discusses the scalar nature of the dot product, the special case of a vector dotted with itself, and how this can be used to define the length of a vector. The paragraph also presents a generalized formula for the angle in any dimension using the dot product. Key properties such as commutativity and the ability to scale the dot product are highlighted. The discussion includes algebraic manipulations to demonstrate these properties and their implications for understanding the dot product in various dimensions.
📐 Proving the Distributive Property of the Dot Product
The paragraph focuses on proving the distributive property of the dot product over vector addition. It uses algebraic methods and vector manipulations to show that the dot product of a vector with the sum of two other vectors is equal to the sum of the dot products of the vector with each of the two vectors individually. The proof involves expressing vectors in terms of their components, expanding using the distributive property, and then simplifying to arrive at the desired result. The proof is emphasized to be true for any coordinate system and number of dimensions.
📉 Deriving the Dot Product in Cartesian Coordinates
This section describes the process of deriving the dot product formula in Cartesian coordinates. It starts by expressing vectors in terms of their Cartesian components and unit vectors. Using the distributive property, the video shows how to expand the dot product of two such vectors into a sum of products of their components. The orthogonality of the unit vectors leads to the simplification of the expression, resulting in the standard formula for the dot product in Cartesian coordinates, which is then added to the 'fact sheet'.
🔄 Derivative of the Dot Product with Respect to Time
The final paragraph addresses the derivative of the dot product when the vectors are functions of time. It outlines the definition of the derivative and applies it to the dot product of two time-varying vectors. The process involves expressing the change in the dot product as the vectors change over a small time interval, using the distributive property to expand the expression, and then taking the limit as the time interval approaches zero. The result is a formula for the derivative of the dot product that resembles the product rule for ordinary functions, and this formula is also added to the 'fact sheet'.
🔚 Conclusion and Future Outlook
In the concluding paragraph, the video script summarizes the findings and sets the stage for future topics. It mentions the next step, which involves using the dot product to define a covariant metric tensor, indicating the progression of the series and the relevance of the dot product to more advanced concepts in tensor calculus.
Mindmap
Keywords
💡Dot Product
💡Tensor Calculus
💡Cartesian Coordinate System
💡Angle Theta
💡Law of Cosines
💡Magnitude
💡Commutative Property
💡Distributive Property
💡Cartesian Coordinates
💡Derivative
💡Covariant Metric Tensor
Highlights
Introduction to the dot product as a prerequisite for tensor calculus.
Critique of the traditional Cartesian coordinate system's definition of the dot product for tensor calculus.
Presentation of an alternate definition for the dot product in tensor calculus.
Derivation of properties of the dot product from the tensor calculus definition.
Use of the law of cosines to calculate the magnitude of vector a minus b.
Demonstration of how to find the angle between transported vectors using supplementary angles.
Application of the law of cosines to find the magnitude of the sum of vectors a and b.
Derivation of the alternate definition of the dot product using algebraic manipulation.
Introduction of a fact sheet to track discoveries about the dot product.
Explanation of the dot product producing a scalar value and its implications.
Special case analysis of the dot product of a vector with itself for defining vector length.
Generalized formula for calculating an angle in any dimension using the dot product.
Proof of the commutative property of the dot product through algebraic expression.
Discussion on scaling the dot product and its algebraic representation.
Algebraic proof of the distributive property of the dot product over vector addition.
Derivation of the dot product in Cartesian coordinates using unit vectors.
Introduction to the derivative of the dot product and its significance.
Proof of the derivative of the dot product using the definition of the derivative and limits.
Finalization of the formula for the derivative of the dot product and its similarity to the product rule for functions.
Anticipation of using the dot product to define a covariant metric tensor in future videos.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: