Mean, Median, Mode, and Outliers: Measures of Central Tendency

Psych Explained
19 Jun 202112:55
EducationalLearning
32 Likes 10 Comments

TLDRThis video from 'Psych Explain' explores the concepts of mean, median, and mode—key measures of central tendency used to identify the center of a data set. It explains how to calculate each measure using sleep hours as an example and discusses when to use each, emphasizing their utility in understanding data clustering. The video also highlights the importance of median over mean in the presence of outliers and the unique ability of mode to represent nominal data, providing practical examples from sports and housing prices.

Takeaways
  • 📊 The video discusses three measures of central tendency: mean, median, and mode, which are used to describe where data clusters around the center.
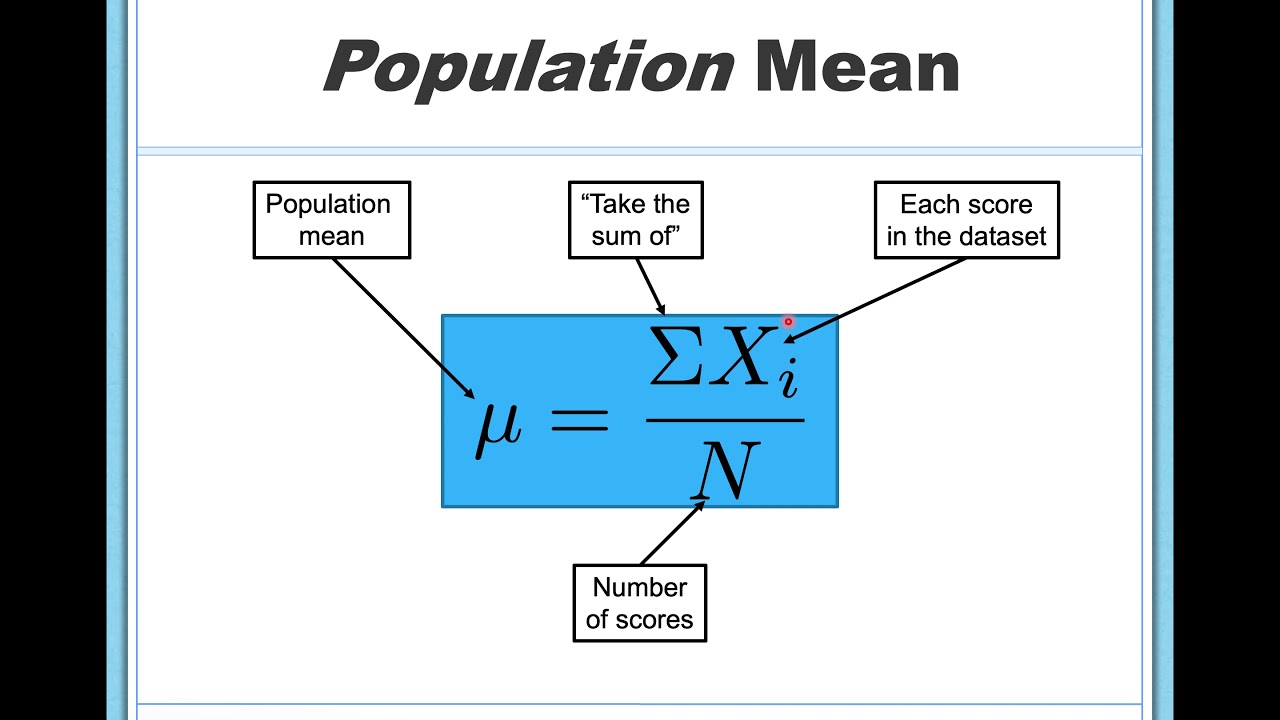
  • 🔢 The mean is the arithmetic average of all data points and is calculated by summing all values and dividing by the number of data points.
  • 📈 The median is the middle value in a data set when arranged in numerical order and is used when data has outliers.
  • 🏁 The mode is the most frequently occurring value in a data set and can represent both numerical and categorical data.
  • 🤔 The choice between mean, median, and mode depends on the data set's characteristics, such as the presence of outliers.
  • 🏠 An example given in the video is using the median for house prices, as it is less affected by extremely high or low values.
  • 📈 Outliers can skew the mean, making it less representative of the data set's central tendency compared to the median.
  • 📊 The video provides a practical example using sleep hours data to illustrate how to calculate the mean, median, and mode.
  • 🔑 The mode can be used to identify the most common category in nominal or categorical data, such as the most popular sports team among fans.
  • 📚 The video emphasizes the importance of understanding when to use each measure for accurately representing data.
  • 📝 The script concludes with a practice problem for viewers to apply the concepts of mean, median, and mode to a new data set.
Q & A

  • What are the three measures of central tendency discussed in the video?

    -The three measures of central tendency discussed in the video are the mean, the median, and the mode.

  • Why are the mean, median, and mode often discussed together?

    -The mean, median, and mode are often discussed together because they all help explain where the data is clustering around or where the center of the data is.

  • What is the mean and how is it calculated?

    -The mean is considered the average or arithmetic average of a data set. It is calculated by adding up all the individual data points and then dividing the sum by the total number of data points.

  • Under what circumstances would the mean be the best measure of central tendency to use?

    -The mean is the best measure of central tendency to use when all the data points are relatively the same, and there are no outliers.

  • What is the median and how is it found?

    -The median is the middle value in a data set when the numbers are arranged in numerical order. If there is an odd number of data points, the median is the middle number. If there is an even number of data points, the median is the average of the two middle numbers.

  • Why would the median be preferred over the mean in certain situations?

    -The median is preferred over the mean when there are outliers in the data set, as it is less affected by extreme values and provides a better representation of the central tendency.

  • What is the mode and how is it determined?

    -The mode is the most frequent number in a data set. It is determined by identifying the data point that occurs most often.

  • Can there be no mode or multiple modes in a data set?

    -Yes, there can be no mode if no number repeats, or there can be multiple modes if two or more numbers repeat with the same frequency.

  • Why is the mode unique among the measures of central tendency?

    -The mode is unique because it can represent not just numbers, but also categories or nominal data, making it versatile for different types of data analysis.

  • What is an example of using the mode in a non-numerical context?

    -An example of using the mode in a non-numerical context is determining the most popular sports team among a group of fans, where the team with the most supporters is the mode.

  • What is the purpose of the practice problem provided at the end of the video?

    -The purpose of the practice problem is to allow viewers to apply the concepts of mean, median, and mode to a data set and test their understanding of these measures of central tendency.

Outlines
00:00
📊 Introduction to Measures of Central Tendency

The video script introduces the concepts of mean, median, and mode, which are measures of central tendency used to describe the center or middle of a data set. It explains that these measures help to understand where data clusters around, as opposed to measures like standard deviation that explain variability. The script outlines the purpose of the video, which is to discuss what the mean, median, and mode are, how to find them, and when to use each measure. An example data set of hours of sleep is presented to illustrate the concepts.

05:00
🔢 Understanding the Mean and Its Calculation

This paragraph delves into the concept of the mean, also known as the average or arithmetic average. It is described as the most common measure of central tendency. The script explains how to calculate the mean through a two-step process: summing all individual data points and then dividing by the total number of data points. The example of calculating the mean from a weekly sleep data set is used to illustrate the process. The paragraph also discusses when to use the mean, which is when all data points are relatively the same, and when not to use it, such as in the presence of outliers.

10:03
🏠 The Median as a Measure of Central Tendency

The script explains the median as the middle value in a data set when arranged in numerical order. It provides a step-by-step guide on how to find the median, whether the data set has an odd or even number of values. The paragraph uses the example of home prices to illustrate the impact of outliers on the mean and why the median is a better measure of central tendency in such cases. It emphasizes that the median is often used in real estate listings and sports statistics to provide a more accurate representation of data when outliers are present.

📈 The Mode and Its Relevance in Data Analysis

The final paragraph introduces the mode as the most frequent number in a data set. It explains that the mode can be used to analyze both numerical and categorical data, making it unique among the measures of central tendency. The script provides examples of how the mode can represent categories such as gender in a study or sports team fandom in a poll. It also discusses the possibility of having no mode, one mode, or multiple modes in a data set. The paragraph concludes with a practice problem for viewers to apply their understanding of mean, median, and mode.

Mindmap
Keywords
💡Mean
The 'mean' is defined as the average of a set of numbers, calculated by summing all the values and then dividing by the number of values. It is a measure of central tendency that indicates the central point of a data set. In the video, the mean is used to describe the arithmetic average of hours of sleep per night over a week, serving as an example to illustrate how to calculate it and its relevance in understanding data clustering.
💡Median
The 'median' is the middle value in a data set that has been arranged in ascending order. It is another measure of central tendency and is particularly useful when the data set contains outliers. The video explains how to find the median by arranging the hours of sleep data in numerical order and identifying the central value, which in the example provided was eight hours.
💡Mode
The 'mode' is the most frequently occurring value in a data set. It is the only measure of central tendency that can represent categorical data and does not necessarily have to be a number. In the script, the mode is illustrated by identifying the number that appears most often in the sleep data set, which is eight hours, and is used to show how it can also apply to non-numerical data, such as the most popular sports team among fans.
💡Measures of Central Tendency
Measures of central tendency are statistical measures that describe the center of a data set. The video focuses on three such measures: mean, median, and mode. These measures are essential for understanding where the data is clustering around or identifying the middle of the data, which is a central theme of the video.
💡Outliers
An 'outlier' is a data point that is significantly different from other data points in a data set, often skewing the results of statistical measures like the mean. The video script uses the example of house prices to illustrate how an outlier can distort the mean, making the median a more representative measure of central tendency in such cases.
💡Data Clustering
The term 'data clustering' refers to the grouping of data points around certain values. The video emphasizes how the mean, median, and mode help explain where data is clustering around, which is crucial for understanding the central tendencies within a data set.
💡Arithmetic Average
The 'arithmetic average' is a term synonymous with the mean, which is calculated by adding up all the values in a data set and dividing by the number of values. The video script uses the concept of the arithmetic average to explain the calculation of the mean for a set of sleep hours.
💡Nominal Data
Nominal data refers to categorical data that can be labeled but not ordered numerically. The video script mentions nominal data in the context of using the mode to identify the most common category, such as the most popular sports team among fans.
💡Categorical Data
Categorical data is a type of data that consists of categories or groups. The mode is the only measure of central tendency that can be applied to categorical data, as it identifies the most common category within the data set, such as the most frequent sports team preference in a poll.
💡Standard Deviation
The 'standard deviation' is a measure of the amount of variation or dispersion in a set of values. Although not the main focus of the video, it is mentioned as a measure that explains what is happening away from the center of the data, in contrast to the mean, median, and mode which describe the center.
💡Bell Curve
A 'bell curve' is a graphical representation of a data set that is symmetrically distributed around its mean, with values falling off on either side. The video uses the bell curve as an example to illustrate how the mean, median, and mode can help explain what is happening in the center of the data.
Highlights

The video discusses the mean, median, and mode as measures of central tendency in psychology.

These measures help explain where data clusters around or the center of the data.

The mean is the arithmetic average, commonly used in various real-life scenarios.

Calculating the mean involves summing all data points and dividing by the total count.

The mean is best used when all data points are relatively the same, without outliers.

The median is the middle value in a data set, representing the 50th percentile.

To find the median, data must be ordered from least to greatest.

The median is used when there are outliers in the data set.

An example of skewed data by an outlier is given with housing prices.

The mode is the most frequent number in a data set, which may not always be numerical.

The mode can represent categories, such as the most common gender in a study.

The mode provides information about nominal or categorical data.

The video provides a practical example of calculating mean, median, and mode using sleep hours.

A practice problem with a data set is presented for viewers to calculate mean, median, and mode themselves.

The video emphasizes the importance of choosing the right measure of central tendency based on data characteristics.

The mean, median, and mode are collectively referred to as measures of central tendency.

The video explains why the median is a better measure than the mean in the presence of outliers.

The mode can indicate the most popular category, such as sports team preferences.

Transcripts

Browse More Related Video

Measures of Central Tendency (Mean, Median, Mode)

Understanding Central Tendency

Mean, Median and Mode - Measures of Central Tendency

Mean, Median and Mode in Statistics | Statistics Tutorial | MarinStatsLectures

Finding mean, median, and mode | Descriptive statistics | Probability and Statistics | Khan Academy

Analyzing Sets of Data: Range, Mean, Median, and Mode

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MeanMedianModeData AnalysisCentral TendencyPsychologyStatisticsDescriptive StatsOutliersTutorial