Mean, Median and Mode - Measures of Central Tendency

DATAtab
12 Nov 202303:25
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into measures of central tendency, such as mean, median, and mode, explaining their calculation and significance in data analysis. The mean is calculated by dividing the sum of observations by their count, exemplified by a mean test score of 86.6 from scores 85, 90, 78, 92, and 88. The median is the middle value in an ordered set, unaffected by outliers, unlike the mean. The mode is the most frequent value in a data set, with sets being classified as unimodal, bimodal, multimodal, or having no mode. The script also contrasts these with measures of dispersion, like standard deviation and range, which describe data spread around the central point. The video aims to clarify the role of central tendency measures in identifying a central value around which data points cluster.

Takeaways
  • 📊 Measures of central tendency include the mean, median, and mode, which are used to find a central value in a dataset.
  • 🧮 The arithmetic mean is calculated by summing all observations and dividing by the number of observations.
  • 📚 An example given was calculating the mean test score of five students, which was found to be 86.6.
  • 🔢 The median is the middle value in a dataset when arranged in ascending order, and is resistant to outliers.
  • 👥 With an odd number of data points, the median is the single middle value, and with an even number, it's the average of the two middle values.
  • 📏 The median is not affected by extreme values, unlike the mean, which can be skewed by outliers.
  • 🔠 The mode is the value that appears most frequently in a dataset and can be used to identify common occurrences.
  • 🎲 A dataset can be unimodal (one mode), bimodal (two modes), multimodal (more than two modes), or have no mode at all.
  • 🌐 Measures of dispersion, such as standard deviation, range, and interquartile range, describe the spread of data points around the central value.
  • 🔄 Measures of central tendency help identify a central value, while measures of dispersion indicate how spread out the data is.
  • 📈 Both central tendency and dispersion measures are important for understanding the characteristics of a dataset.
Q & A

  • What are measures of central tendency?

    -Measures of central tendency are statistical measures that identify the central position within a data set. They include mean, median, and mode.

  • What is the arithmetic mean and how is it calculated?

    -The arithmetic mean is the average of a set of numerical values. It is calculated by summing all the observations and then dividing by the number of observations.

  • Can you provide an example of calculating the mean score from the transcript?

    -Sure. If we have test scores of 85, 90, 78, 92, and 88, the mean score is calculated as (85 + 90 + 78 + 92 + 88) / 5, which equals 86.6.

  • How is the median defined and how do you find it in a data set?

    -The median is the middle value in a data set when the numbers are arranged in ascending order. If there is an odd number of data points, the median is the middle one. If there is an even number, it's the average of the two middle values.

  • Why is the median considered resistant to extreme values or outliers?

    -The median is resistant to outliers because it represents the middle value of a data set, unaffected by the high or low extremes. It remains the same even if the values at the ends change.

  • What is the mode and how does it differ from the mean and median?

    -The mode is the value that appears most frequently in a data set. It differs from the mean and median as it focuses on the most common value rather than the average or middle value.

  • What are the different types of modality in a data set?

    -A data set can be unimodal (one mode), bimodal (two modes), multimodal (more than two modes), or have no mode if all values appear with the same frequency.

  • How does the mode differ in a data set with no repeating values?

    -In a data set with no repeating values, there is no mode because no value appears more frequently than the others.

  • What is the difference between measures of central tendency and measures of dispersion?

    -Measures of central tendency provide a single value that represents the entire data set, identifying a central value around which data points cluster. Measures of dispersion, on the other hand, indicate how spread out the data points are, showing whether they are closely packed around the center or spread far from it.

  • Can you give an example of a measure of dispersion?

    -Examples of measures of dispersion include standard deviation, range, and interquartile range. These measures help to understand the spread or variability within a data set.

  • Why are measures of central tendency and dispersion important in data analysis?

    -Measures of central tendency and dispersion are important because they help to summarize and interpret data. Central tendency provides a central point, while dispersion describes how the data is spread around that center, giving insights into the data's variability and distribution.

Outlines
00:00
📊 Understanding Measures of Central Tendency

This paragraph introduces the concept of measures of central tendency, specifically focusing on the mean, median, and mode. The mean is defined as the sum of all observations divided by the number of observations, and an example is provided using test scores of five students, resulting in a mean score of 86.6. The median is explained as the middle value of a data set when arranged in ascending order, with special attention given to its resistance to outliers. The mode is described as the most frequently occurring value in a data set, with examples given for unimodal, bimodal, multimodal, and non-modal data sets. The paragraph ends with a brief comparison between measures of central tendency and measures of dispersion, highlighting their roles in representing a central value and describing the spread of data points, respectively.

Mindmap
Keywords
💡Measures of Central Tendency
Measures of central tendency are statistical values that represent a single value for a data set, which can be used to describe the center point of the data. In the context of the video, these measures are crucial for understanding the main theme, which is to provide a central value around which data points tend to cluster. The video mentions three types of measures of central tendency: mean, median, and mode, each serving as a different way to represent the 'middle' of a data set.
💡Arithmetic Mean
The arithmetic mean, often referred to simply as the 'mean,' is calculated by adding all the values in a data set and then dividing by the number of values. It is a fundamental measure of central tendency. In the video, the mean is exemplified by calculating the average test score of five students (85, 90, 78, 92, and 88), which results in a mean score of 86.6. This calculation illustrates how the mean can provide a single value that represents the entire set of scores.
💡Median
The median is another measure of central tendency and is defined as the middle value in a data set when the values are arranged in ascending order. If there is an odd number of data points, the median is the exact middle value, while for an even number, it is the average of the two middle values. The video highlights the robustness of the median against outliers, as it remains unaffected by extreme values, unlike the mean.
💡Mode
The mode is the value that appears most frequently in a data set. It is a measure of central tendency that can be used when the data set is not numerical or when different types of data need to be compared. The video explains that a data set can be unimodal (one mode), bimodal (two modes), multimodal (more than two modes), or have no mode at all, depending on the frequency of the values.
💡Outliers
Outliers are data points that are significantly different from other observations, often skewing the results of statistical measures like the mean. The video script points out that the median is resistant to the influence of outliers, making it a more reliable measure of central tendency when extreme values are present.
💡Data Set
A data set refers to a collection of data points that are often used for statistical analysis. In the video, the term is used to describe the test scores of students and the blood pressure measurements of patients. The data set is the basis for calculating measures of central tendency and dispersion.
💡Resistant to Extreme Values
The term 'resistant to extreme values' refers to the property of certain statistical measures, like the median, to remain unaffected by outliers or extreme data points. The video uses this concept to contrast the median with the mean, emphasizing the median's stability in the presence of outliers.
💡Unimodal, Bimodal, Multimodal
These terms describe the number of modes in a data set. A data set is 'unimodal' if it has one mode, 'bimodal' if it has two modes, and 'multimodal' if it has more than two modes. The video uses these terms to categorize different types of data sets based on the frequency of their values.
💡Measures of Dispersion
Measures of dispersion, such as standard deviation, range, and interquartile range, provide information about the spread of data points in a data set. The video contrasts these with measures of central tendency, explaining that while central tendency provides a central point, dispersion measures describe how the data is spread around that center.
💡Blood Pressure
Blood pressure is used in the video as an example to illustrate how measures of central tendency and dispersion can be applied to real-world data. It serves as a practical context for understanding how these statistical measures can be used to analyze and interpret health-related data.
Highlights

Measures of central tendency include mean, median, and mode.

Arithmetic mean is calculated by dividing the sum of all observations by the number of observations.

Example given: Mean test score of five students is 86.6.

Median is the middle value in a data set when arranged in ascending order.

Median is resistant to extreme values or outliers.

Mode is the value that appears most frequently in a data set.

A dataset with one mode is called unimodal.

A dataset with two modes is called bimodal.

A dataset can be multimodal with more than two modes.

A dataset with no repeating values has no mode.

Measures of central tendency provide a single value representing the entire dataset.

Measures of dispersion, like standard deviation, indicate how spread out the data points are.

Central tendency measures help identify a central value around which data points cluster.

Measures of dispersion describe how the dataset is spread around the central point.

Video aims to explain the importance and application of measures of central tendency and dispersion.

Transcripts

Browse More Related Video

Finding mean, median, and mode | Descriptive statistics | Probability and Statistics | Khan Academy

Mode, Median, Mean, Range, and Standard Deviation (1.3)

An Average Video | Mean, Median, Mode, and Range

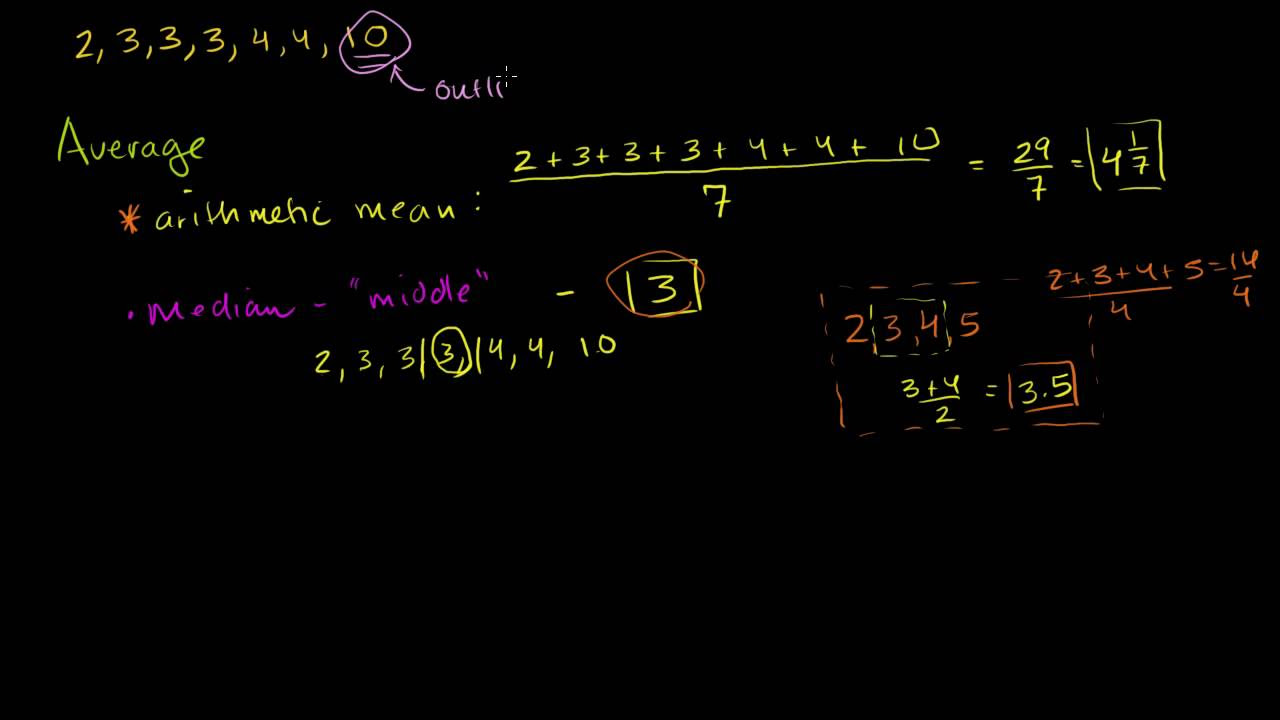
Average or Central Tendency: Arithmetic Mean, Median, and Mode

How to Find the Mean, Median, Mode, and Range

Mean, Median, and Mode: Measures of Central Tendency: Crash Course Statistics #3

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Central TendencyArithmetic MeanMedianModeData AnalysisStatistical ConceptsOutliersEducational ContentMeasures of DispersionStandard DeviationInterquartile Range