How to show that a solution exists to a functions using IVT

Brian McLogan
3 Dec 201704:00
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses proving the existence of a solution for the function f(x) = x^5 - x - 2 on the closed interval [0, 2]. It emphasizes the importance of the Intermediate Value Theorem (IVT), which states that a continuous function on a closed interval will take on all values between its endpoints. The script demonstrates that since f(0) is negative and f(2) is positive, there must be at least one zero between these points due to the function's continuity. The explanation is aimed at showing that a solution exists without pinpointing its exact location, relying on the IVT for the proof.

Takeaways
  • 📚 The script discusses proving the existence of a solution for a continuous function on a closed interval.
  • 🔍 The function in question is \( f(x) = x^5 - x - 2 \), and the interval is from 0 to 2.
  • 📉 The script uses the Intermediate Value Theorem (IVT) to argue that a solution exists within the interval.
  • 📌 The IVT states that if a function is continuous on a closed interval and changes sign, there must be a root within that interval.
  • 🔢 The script checks the function's values at the endpoints of the interval: \( f(0) = -2 \) and \( f(2) = 28 \).
  • 📈 The function values at the endpoints show a sign change from negative to positive, satisfying the IVT's conditions.
  • 🤔 The script suggests that the exact location of the root is not necessary to prove its existence, only that it exists.
  • 🛠 The script mentions using technology to find the root but clarifies that it's not required for the proof.
  • 📝 The conclusion is that by the IVT, there must be a solution where \( f(x) = 0 \) within the interval [0, 2].
  • 📑 The script provides a structured argument for the proof, using continuity and the function's behavior at the interval's endpoints.
  • 📈 The script emphasizes the importance of continuity and a closed interval for the IVT to apply.
Q & A

  • What function is being discussed in the script?

    -The function being discussed is f(x) = x to the fifth minus x minus two.

  • What is the interval over which the function is being analyzed?

    -The interval is from 0 to 2, which is a closed interval.

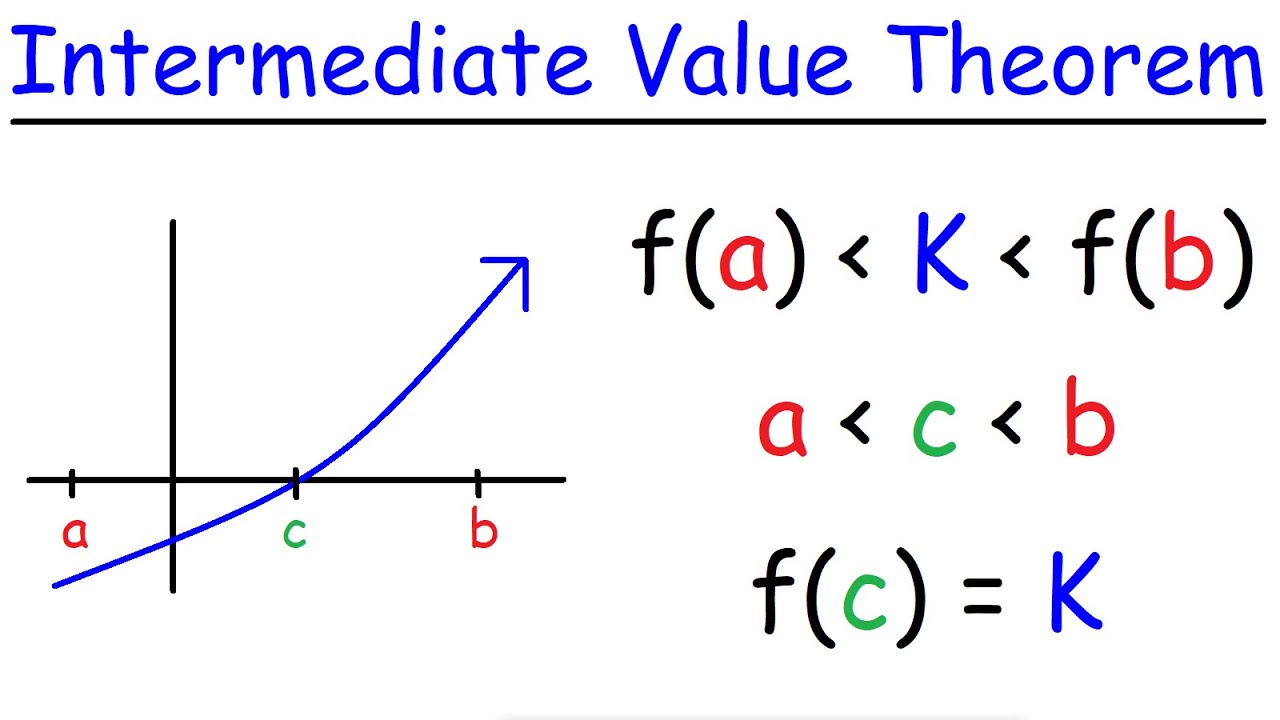
  • Why is the Intermediate Value Theorem (IVT) relevant to this discussion?

    -The IVT is relevant because it states that if a function is continuous on a closed interval and takes on two values, then it also takes on all values in between, including zero if the function is being analyzed for roots.

  • What is the value of the function at x = 0?

    -At x = 0, the function evaluates to f(0) = 0^5 - 0 - 2, which equals -2.

  • What is the value of the function at x = 2?

    -At x = 2, the function evaluates to f(2) = 2^5 - 2 - 2, which equals 28.

  • Why is it not necessary to find the exact point where the function crosses the x-axis?

    -It is not necessary because the task is to prove the existence of a solution (a root), not to find its exact location. The IVT guarantees the existence of at least one solution in the interval.

  • What does the script imply about the continuity of the function?

    -The script implies that the function is continuous on the interval [0, 2], which is a prerequisite for applying the IVT.

  • What is the conclusion drawn from the values of the function at the endpoints?

    -The conclusion is that since the function has a negative value at x = 0 and a positive value at x = 2, and given the function is continuous, there must be at least one root in the interval (0, 2) by the IVT.

  • What is the significance of the function being continuous on a closed interval for the IVT?

    -The continuity of the function on a closed interval is crucial for the IVT because it ensures that the function will take on all values between its minimum and maximum on that interval, including zero if the function changes sign.

  • How does the script suggest we can find the root of the function?

    -The script suggests that while the exact root can be found using technology, the proof of existence is based on the IVT and does not require the root's exact location.

  • What is the final statement in the script regarding the existence of a solution?

    -The final statement confirms that by the IVT, there must be a solution (a value of x where f(x) = 0) between 0 and 2, even though the exact solution is not provided.

Outlines
00:00
📚 Proving Existence of a Solution Using IVT

The paragraph discusses the application of the Intermediate Value Theorem (IVT) to prove the existence of a solution for the function f(x) = x^5 - x - 2 on the closed interval [0, 2]. The speaker asserts that since the function is continuous on the interval and we have a negative value at x=0 and a positive value at x=2, the IVT guarantees a crossing of the x-axis, indicating the presence of a root within the interval. The speaker emphasizes the importance of continuity and the closed nature of the interval in applying the IVT, and concludes by stating that while the exact location of the root is not determined, its existence is guaranteed by the theorem.

Mindmap
Keywords
💡Solution
In the context of the video, 'solution' refers to the value(s) of 'x' for which the function 'f(x) = x^5 - x - 2' equals zero. The video aims to prove the existence of such a value on the interval [0, 2]. The script uses the Intermediate Value Theorem (IVT) to argue that since the function is continuous and changes sign over the interval, at least one solution must exist where the function crosses the x-axis.
💡Function
A 'function' in mathematics is a relation between a set of inputs and a set of permissible outputs, with the property that each input is related to exactly one output. In the video, the function 'f(x) = x^5 - x - 2' is the focus, and the script discusses its continuity and behavior over the interval [0, 2] to prove the existence of a solution.
💡Continuous
A function is 'continuous' if, roughly speaking, it has no abrupt changes in value, meaning that it does not have any jumps or breaks in its graph. The script emphasizes the continuity of the function 'f(x)' as a prerequisite for applying the IVT, which is crucial for the argument presented in the video.
💡Closed Interval
A 'closed interval' in mathematics is a set of numbers that includes all the numbers between two endpoints, including the endpoints themselves. In the video, the interval [0, 2] is a closed interval where the existence of a solution to the function is being discussed.
💡Intermediate Value Theorem (IVT)
The 'Intermediate Value Theorem' is a fundamental theorem in calculus that states if a function is continuous on a closed interval and takes on different signs at the endpoints, then it must take on every value in between at some point within the interval. The script uses the IVT to argue for the existence of a root of the function within the interval [0, 2].
💡Endpoints
In the context of an interval, 'endpoints' refer to the first and last values of the interval. The script checks the values of the function at the endpoints of the interval [0, 2], which are f(0) and f(2), to demonstrate the change in sign necessary for the IVT to be applicable.
💡Root
A 'root' of a function is a value of 'x' for which the function equals zero. The video script is focused on proving the existence of a root for the function 'f(x) = x^5 - x - 2' within the given interval, using the IVT.
💡Change in Sign
A 'change in sign' refers to the situation where a function's value switches from positive to negative or vice versa. The script notes that the function changes sign from negative at x=0 to positive at x=2, which is a key observation for applying the IVT.
💡Graph
In the script, the 'graph' of the function is implied when discussing the behavior of the function and its continuity. The graph is a visual representation of the function, with the x-axis representing the input values and the y-axis representing the output values. The script suggests that the function's graph does not intersect the x-axis at the endpoints but must somewhere in between due to the IVT.
💡Technology
The script briefly mentions the use of 'technology' as a means to find the exact location of the solution, although the main point of the video is to prove the existence of a solution without necessarily finding its exact value. This suggests that while technology can assist in locating the root, the proof of its existence is independent of such tools.
Highlights

The function f(x) = x^5 - x - 2 is being analyzed for a solution on the interval [0, 2].

The function is assumed continuous on the closed interval, which is a prerequisite for applying the Intermediate Value Theorem (IVT).

The IVT is introduced as the main tool to prove the existence of a solution without needing to find the exact value.

The function's behavior at the endpoints of the interval is examined, with f(0) = -2 and f(2) = 28.

A negative value at x=0 and a positive value at x=2 indicates the function must cross the x-axis within the interval.

The IVT guarantees the existence of at least one solution where f(x) = 0 on the closed interval [0, 2].

The proof does not require the exact location of the solution, only the assurance of its existence.

The function's continuity is confirmed, which is essential for the application of the IVT.

The function's values at the endpoints are compared to demonstrate the change from negative to positive.

The existence of a solution is concluded based on the IVT, given the function's continuity and the interval's properties.

The proof leverages the fact that the function changes sign between the endpoints, indicating a root within the interval.

Technology could be used to find the exact solution, but the task only requires proving its existence, not its location.

The proof is structured by establishing the necessary conditions for the IVT: continuity, a closed interval, and sign change.

The conclusion is reached that a solution exists due to the function's behavior and the IVT's assurance.

The proof is summarized, emphasizing the IVT's role in establishing the existence of a solution without pinpointing its exact value.

The method demonstrates a practical application of the IVT in proving the existence of solutions for continuous functions on closed intervals.

Transcripts

Browse More Related Video

Intermediate Value Theorem, calculus 1 tutorial, showing a root of a function on an interval

Using the Intermediate Value Theorem Examples

Intermediate value theorem example | Existence theorems | AP Calculus AB | Khan Academy

Intermediate Value Theorem: show function has at least one solution -- CALCULUS

AP Calculus Review Three Theorems You Must Know (EVT, IVT, MVT)

Intermediate Value Theorem

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
IVT ProofPolynomial FunctionSolution ExistenceContinuous FunctionClosed IntervalMathematicsRoot FindingAlgebraic AnalysisFunction ContinuityInterval Endpoints