Intermediate Value Theorem

The Organic Chemistry Tutor
21 Feb 201811:03
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the Intermediate Value Theorem (IVT), a fundamental concept in calculus, which asserts that if a function f is continuous on a closed interval [a, b] and k is any number between f(a) and f(b), then there exists at least one number c in the interval such that f(c) equals k. The script applies this theorem to demonstrate the existence of a root or zero within a specified interval for a given function. It illustrates this with examples, showing how to find the values of a and b, and how to identify a specific c that satisfies the theorem. The examples also involve solving equations to pinpoint the exact values of c.

Takeaways
  • 📚 The Intermediate Value Theorem (IVT) states that if a function f is continuous on a closed interval [a, b] and f(a) ≠ f(b), then for any k between f(a) and f(b), there exists at least one c in the interval such that f(c) = k.
  • 🔍 To apply IVT, first determine the values of f(a) and f(b) for the given interval.
  • 🎯 The goal in finding a root is to show that there exists a value c where f(c) = 0 within the specified interval.
  • 🤔 For the function f(x) = x^3 + 4x, f(0) = -2 and f(2) = 14, indicating a continuous function where a root likely exists between 0 and 2.
  • 📈 When f(0) is negative and f(2) is positive, the function must cross the x-axis, confirming the presence of a root.
  • 🌟 For a different function, like f(x) = x^2 + x - 1 on the interval [0, 5], f(0) = -1 and f(5) = 29, and given f(c) = 11, IVT confirms a root exists where f(x) = 11.
  • 📝 To find the specific value of c, set f(x) equal to the desired value (k) and solve for x, factoring and using the interval to determine the correct root.
  • 🔢 For the function f(x) = 2x^2 - 3x + 7 on the interval [0, 3], f(0) = 7 and f(3) = 16, and for k = 9, IVT implies a root exists where f(x) = 9.
  • 🧩 Solving for c involves factoring the equation 2x^2 - 3x + 7 = 9 and simplifying to find the x values that satisfy the equation within the given interval.
  • 🎓 The value of c must be within the interval [a, b]. In the example with f(x) = 2x^2 - 3x + 7, c = 2 is the correct value since it lies within the interval and satisfies f(c) = 9.
  • 📊 The Intermediate Value Theorem is a powerful tool in calculus for proving the existence of roots and zeros of continuous functions within specified intervals.
Q & A

  • What is the Intermediate Value Theorem and how does it relate to finding roots of a function?

    -The Intermediate Value Theorem states that if a function f is continuous on a closed interval [a, b], and f(a) and f(b) have opposite signs (i.e., they do not equal each other), then there exists at least one number c in the interval [a, b] such that f(c) equals zero. This theorem is crucial in demonstrating the existence of a root or zero for a function within a specified interval.

  • How do you determine the values of f(a) and f(b) for a given function?

    -To determine the values of f(a) and f(b), you simply substitute the endpoints of the interval into the function. For example, if a is 0 and b is 2, you would calculate f(0) by plugging 0 into the function and similarly for f(2) by plugging 2 into the function.

  • What is the significance of the number k in the context of the Intermediate Value Theorem?

    -In the context of the Intermediate Value Theorem, k represents the value we are trying to find the root for, which is typically zero when we are looking for a root of the function. The theorem helps us establish that if the function is continuous on the interval and f(a) and f(b) have different values, there must exist a c in that interval such that f(c) = k, where k is between f(a) and f(b).

  • How can you use the Intermediate Value Theorem to prove the existence of a root in a given interval?

    -To use the Intermediate Value Theorem to prove the existence of a root in a given interval, first ensure the function is continuous on that interval. Then, evaluate the function at the interval's endpoints (a and b). If the function values at these endpoints are not equal and k (the value we're checking for, usually zero) is between f(a) and f(b), the theorem guarantees there is at least one c in the interval [a, b] where f(c) = k, indicating the presence of a root.

  • What is the process to find the value of c in the context of the Intermediate Value Theorem?

    -To find the value of c, first, verify that the Intermediate Value Theorem applies by checking that f(a) and f(b) are not equal and that k is between them. Then, set the function equal to k and solve the resulting equation for x. The solutions will give you the possible values of c. Check which of these values fall within the given interval to find the specific c that satisfies the theorem.

  • What is the role of factoring in solving for c in the Intermediate Value Theorem problems?

    -Factoring plays a crucial role in solving for c when using the Intermediate Value Theorem. After setting the function equal to the value k, the resulting polynomial equation is often factored to find the values of x. Factoring the equation breaks it down into simpler linear equations, which can then be easily solved to find the potential values of c.

  • How does the Intermediate Value Theorem help in verifying the existence of a specific value of c within an interval?

    -The Intermediate Value Theorem provides a mathematical basis to confirm the existence of a specific value of c within an interval if the function is continuous and the values at the interval's endpoints straddle the target value k. It ensures that at least one value c within the interval will yield a function value equal to k, which is typically zero when searching for a root.

  • What is the importance of verifying that k is between f(a) and f(b) in the Intermediate Value Theorem?

    -Verifying that k is between f(a) and f(b) is essential because it ensures that the Intermediate Value Theorem can be applied. If k is not between these two values, the theorem does not guarantee the existence of a c that satisfies f(c) = k within the interval, and we cannot conclude that a root exists.

  • How does the Intermediate Value Theorem relate to the concept of continuity in functions?

    -The Intermediate Value Theorem is directly related to the concept of continuity. It states that if a function is continuous on a closed interval [a, b], then it will take on all values between f(a) and f(b). This property of continuity is what allows the theorem to guarantee the existence of a root within the interval if f(a) and f(b) are not equal.

  • What are the necessary conditions for applying the Intermediate Value Theorem?

    -The necessary conditions for applying the Intermediate Value Theorem are that the function must be continuous on the closed interval [a, b], and the function values at the endpoints, f(a) and f(b), must not be equal. Additionally, the value k (which is usually the target value we're checking for, such as zero) must be between f(a) and f(b).

  • What is the process to find the value of c for the given function f(x) = 2x^2 - 3x + 7 on the interval [0, 3] when f(c) is supposed to be equal to 9?

    -First, evaluate the function at the endpoints of the interval. For x=0, f(x) = 7. For x=3, f(x) = 16. Since 9 is between 7 and 16, the Intermediate Value Theorem applies. Now, set the function equal to 9 and solve for x: 2x^2 - 3x + 7 = 9. Rearrange the equation to 2x^2 - 3x - 2 = 0, and factor it to get (2x - 1)(x - 2) = 0. Solve for x to get two potential values: x = 0.5 and x = 2. Since we are looking for a value of c in the interval [0, 3], the valid value for c is 2, where f(2) = 9.

Outlines
00:00
📚 Introduction to the Intermediate Value Theorem

This paragraph introduces the Intermediate Value Theorem (IVT), a fundamental concept in calculus. The theorem states that if a function f is continuous on a closed interval [a, b], and f(a) ≠ f(b), then for any number k between f(a) and f(b), there exists at least one number c in the interval [a, b] such that f(c) = k. The paragraph goes on to apply this theorem to demonstrate the existence of a root or zero within a specified interval. It uses the interval [0, 2] as an example, calculating the values of f(a) and f(b), and explains the process of finding a root where f(c) = 0, emphasizing the continuity of the function and its necessity to cross the x-axis within the interval.

05:02
🔍 Applying IVT to a Specific Function

This paragraph delves into the application of the Intermediate Value Theorem to a specific function, f(x) = x^2 + x - 1, on the interval [0, 5]. It begins by verifying the applicability of the theorem by evaluating f(a) and f(b), resulting in f(0) = -1 and f(5) = 29. The paragraph then sets up the equation f(x) = 11 and solves for x, factoring the quadratic equation to find the potential values of x (c). It correctly identifies the value of c within the interval [0, 5] as the solution, which is c = 3, where f(c) = 11.

10:02
📈 Using IVT to Find a Specific Value of c

The final paragraph presents a problem-solving scenario where the Intermediate Value Theorem is used to find a specific value of c for a given function f(x) = 2x^2 - 3x + 7 on the interval [0, 3]. The paragraph starts by evaluating the function at the endpoints of the interval, finding f(0) = 7 and f(3) = 16. It then sets up the equation to find c such that f(c) = 9, leading to a trinomial equation. The paragraph demonstrates the factoring process, including factoring by grouping, to solve for x and identify the correct value of c within the interval. The solution reveals that c = 2, where f(c) = 9, and confirms that this value is within the specified interval.

Mindmap
Keywords
💡Intermediate Value Theorem
The Intermediate Value Theorem is a fundamental theorem in calculus that states if a function f is continuous on a closed interval [a, b], and k is any number between f(a) and f(b), then there exists at least one number c in the interval [a, b] such that f(c) = k. This theorem is crucial in demonstrating the existence of roots or zeros of a function within a specified interval, as it guarantees that if a function changes sign over an interval, there must be a point where the function equals zero.
💡Continuous Function
A continuous function is one where between any two points on the graph, there are no breaks or jumps; the function's value changes smoothly. This property is essential for the Intermediate Value Theorem to hold, as it ensures that the function will take on every value between f(a) and f(b) if it is continuous on the interval [a, b].
💡Root or Zero
A root or zero of a function is a value of the independent variable (usually x) that makes the function equal to zero. Finding the roots of a function is important in solving equations and understanding the behavior of functions, as it indicates where the graph of the function crosses the x-axis.
💡Closed Interval
A closed interval is a set of numbers on the number line that includes its endpoints. In the context of the Intermediate Value Theorem, a function being continuous on a closed interval [a, b] means that it is continuous from a to b, including the endpoints a and b themselves.
💡Function Evaluation
Function evaluation involves substituting a value into a function to determine the output. It is a fundamental process in understanding how a function behaves at specific points and is used to find values such as f(a) and f(b) when applying the Intermediate Value Theorem.
💡Sign Change
A sign change occurs when the value of a function crosses from being positive to negative or vice versa. Detecting sign changes is critical in finding the roots of a function because the Intermediate Value Theorem guarantees that if there is a sign change over an interval, there is at least one root within that interval.
💡Factoring
Factoring is the process of breaking down a polynomial into a product of other polynomials or factors. It is a common method for solving equations, particularly when finding the roots of a quadratic or higher-degree polynomial function.
💡Greatest Common Factor (GCF)
The Greatest Common Factor (GCF) is the largest factor that a set of numbers or terms shares. In algebra, finding the GCF is useful for simplifying expressions and solving certain types of equations, especially when factoring by grouping.
💡Polynomial
A polynomial is an algebraic expression consisting of variables and coefficients that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. Polynomials are fundamental in algebra and are used to model a wide variety of mathematical relationships.
💡Trinomial
A trinomial is a polynomial with three terms. It is one of the simplest forms of polynomials and can be either a linear trinomial (with a single variable and two constants) or a quadratic trinomial (with a variable squared and two other terms).
💡Solving Equations
Solving equations involves finding the values of the unknown variable that make the equation true. This process is fundamental in mathematics and is used to determine the roots or solutions to algebraic expressions, which can represent a wide range of real-world situations.
Highlights

The Intermediate Value Theorem (IVT) is discussed in detail, providing a foundational understanding of its mathematical principles and implications.

IVT is explained in the context of a function being continuous on a closed interval [a, b], which is a key condition for its applicability.

The theorem's statement is clearly articulated, specifying the existence of at least one number 'c' within the interval [a, b] where f(c) equals any given number 'k' between f(a) and f(b).

An example is provided to demonstrate the application of IVT in finding a root or zero within a specified interval, showcasing its practical utility in solving equations.

The values of f(a) and f(b) are calculated for a specific function, emphasizing the importance of these values in the IVT process.

The concept of 'k' being between f(a) and f(b) is highlighted, which is crucial for the theorem to be applicable.

A step-by-step approach is outlined to apply IVT, including setting f(x) equal to zero to find the root within the given interval.

A new example is introduced, changing the function and interval, to further illustrate the versatility of the IVT.

The verification process of IVT's applicability to a given interval is explained, emphasizing the need to evaluate f(a) and f(b).

The method to find the value of 'c' guaranteed by IVT is demonstrated, involving setting the function equal to the specific 'k' value and solving for 'x'.

The importance of 'c' being within the interval [a, b] is reiterated, ensuring the solution's validity according to IVT.

A problem is presented for the audience to solve, encouraging active engagement with the material and promoting a deeper understanding of IVT.

The process of evaluating the function at points 'a' and 'b' is detailed, providing a clear framework for applying IVT to new scenarios.

The necessity of 'k' being between the values of the function at 'a' and 'b' is underscored, for the theorem to be effective.

A comprehensive walkthrough is given for solving the equation to find 'c', including factoring and setting factors equal to zero.

The selection process for the correct 'c' value is explained, ensuring it falls within the specified interval and meets the theorem's requirements.

The final answer is provided, with 'c' being the value within the interval that makes f(c) equal to the specified 'k', reinforcing the theorem's utility.

Transcripts

Browse More Related Video

Using the Intermediate Value Theorem Examples

Calculus 1 Lecture 3.2: A BRIEF Discussion of Rolle's Theorem and Mean-Value Theorem.

Intermediate value theorem example | Existence theorems | AP Calculus AB | Khan Academy

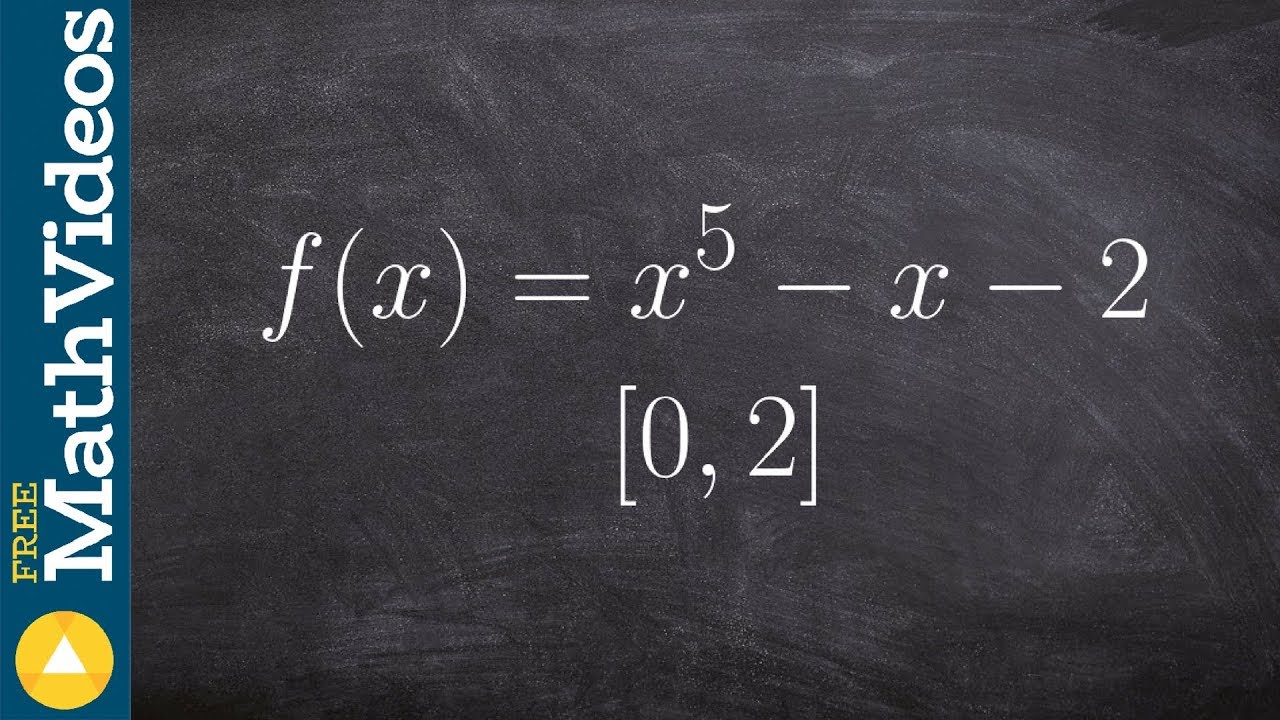
How to show that a solution exists to a functions using IVT

Mean Value Theorem

Justification with the intermediate value theorem: table | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsTheoremApplicationContinuousFunctionsRootFindingIntervalAnalysisEducationalContentProblemSolvingAlgebraicMethodsMathTutorialsMathematicsEducation