Using the Intermediate Value Theorem Examples
TLDRThe video script delves into the concept and application of the Intermediate Value Theorem (IVT), a fundamental principle in calculus. It explains that if a function, f(x), is continuous on a closed interval [a, b] and f(a) ≠ f(b), then for any value M between f(a) and f(b), there exists a point c within the open interval (a, b) where f(c) = M. The script illustrates how IVT can be used to prove the existence of solutions without necessarily finding them, which is often sufficient for many mathematical proofs. The presenter demonstrates the theorem's utility by solving two problems: one involving continuous functions f(x) and g(x) to show that f(x) = g(x) for some x between -2 and 8, and another to determine the minimum number of times a function equals zero on a given interval. The video emphasizes the importance of continuity and the theorem's role in establishing the existence of at least a certain number of solutions, providing a solid foundation for further exploration in calculus.
Takeaways
- 📌 The Intermediate Value Theorem (IVT) is applicable when a function f(x) is continuous on a closed interval [a, b].
- 📌 For IVT to be used, f(a) and f(b) must not be equal; they can be any values except the same value.
- 📌 If f(a) ≠ f(b), there exists at least one c in the open interval (a, b) such that f(c) equals any given y-value between f(a) and f(b).
- 📌 The value of c guaranteed by IVT exists only on the open interval (a, b), not at the endpoints.
- 📌 IVT allows us to prove the existence of a solution without necessarily finding it.
- 📌 Continuity of the function on the closed interval is a crucial requirement for IVT to be applicable.
- 📌 A new function H(x) can be defined as the difference of two continuous functions f(x) and g(x) to apply IVT.
- 📌 By calculating values of H(x) at given points and using IVT, one can prove that f(x) = g(x) for some x in a certain interval.
- 📌 IVT can be used to determine the minimum number of times a function equals zero on a given interval, if the function changes sign.
- 📌 The theorem is a powerful tool in calculus, often used in proofs and can appear in exams like the AP Calculus exam.
- 📌 When using IVT, it's important to articulate the reasoning clearly, as the process of applying the theorem is part of the answer.
Q & A
What is the Intermediate Value Theorem?
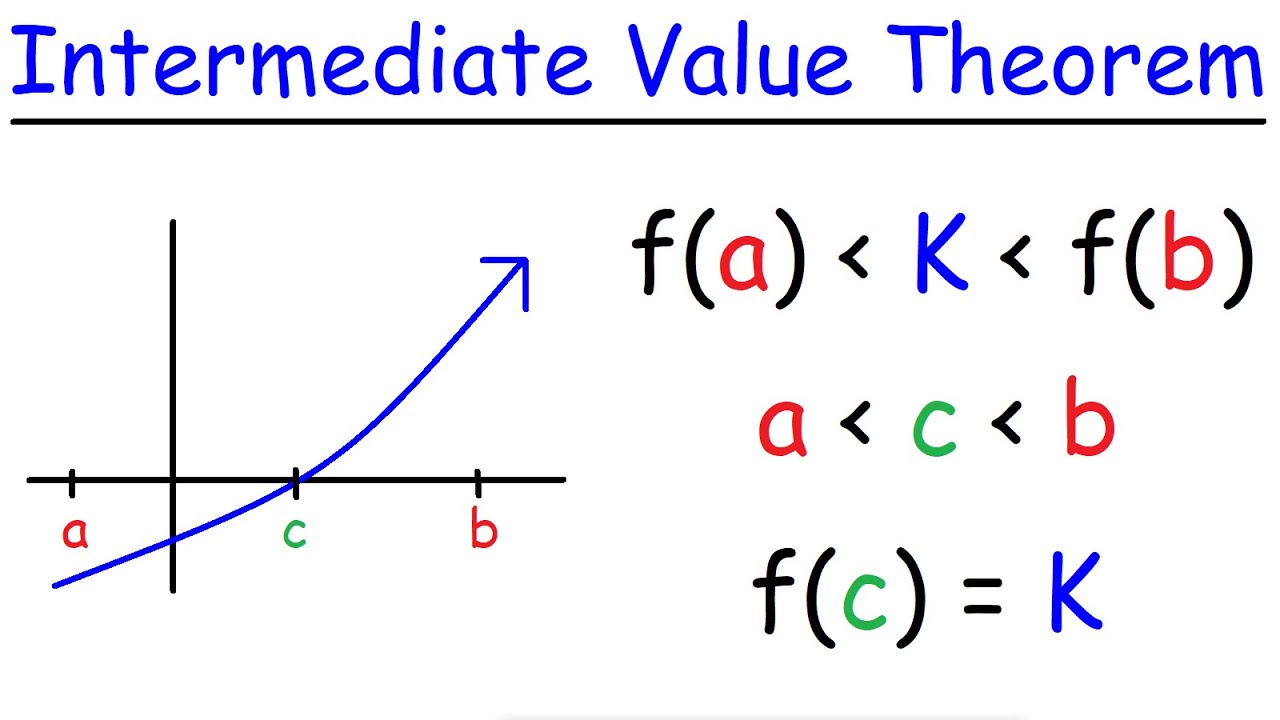
-The Intermediate Value Theorem states that if a function f(x) is continuous on a closed interval [a, b] and f(a) and f(b) are not equal, then for every value between f(a) and f(b), there exists at least one value c in the open interval (a, b) such that f(c) equals that value.
Why is continuity important for the Intermediate Value Theorem?
-Continuity is crucial because the theorem only applies to functions that are continuous on the closed interval [a, b]. If the function is not continuous, the theorem cannot guarantee the existence of a value c that satisfies the condition.
What does it mean for f(a) and f(b) to not be equal in the context of the theorem?
-For the theorem to apply, the function values at the endpoints a and b must not be the same. This ensures that there is a range of y-values between f(a) and f(b) where the function could potentially take on any value, including the one we are interested in.
How does the theorem help in proving the existence of a solution without finding it?
-The theorem allows us to assert that a solution exists within a given interval without explicitly finding it. This is particularly useful in complex problems where finding the solution directly may be difficult or impossible.
Can you provide an example of how to apply the Intermediate Value Theorem to a problem?
-Sure. Given two continuous functions f(x) and g(x) with known values at certain points, you can define a new function h(x) = f(x) - g(x). If h(x) is continuous and h(a) and h(b) have opposite signs, by the theorem, h(x) must equal zero for some x in the open interval (a, b), which implies that f(x) = g(x) for that x.
What is the significance of the value of c being only guaranteed to exist on the open interval (a, b)?
-The value of c is guaranteed to exist within the open interval (a, b) because that's where the function is guaranteed to take on all values between f(a) and f(b). The endpoints a and b themselves are not included in this guarantee because the theorem requires the function to change values within the interval.
How does the Intermediate Value Theorem relate to the graph of a continuous function?
-The theorem implies that if you draw a horizontal line on the graph of a continuous function at any y-value between f(a) and f(b), there will be at least one point where the line intersects the graph within the open interval (a, b).
What is the minimum number of times a continuous function f(x) must equal zero on a closed interval if f(1) and f(4) are not zero?
-If f(x) is continuous and f(1) and f(4) are not zero, and if there are values within the interval (1, 4) where the sign of f(x) changes, then by the Intermediate Value Theorem, f(x) must equal zero at least once on each of these intervals where the sign change occurs.
How can you determine the minimum number of times f(x) equals zero on a closed interval using the Intermediate Value Theorem?
-You can determine the minimum number by identifying points where the function values have different signs. Each sign change indicates at least one zero between those points due to the theorem. The actual number of zeros could be higher, but the theorem guarantees at least that many.
What is the role of the new function h(x) = f(x) - g(x) in applying the Intermediate Value Theorem?
-The new function h(x) is used to combine the properties of two continuous functions f(x) and g(x). If h(x) is continuous and h(a) and h(b) have opposite signs, then by the theorem, there exists some c in the open interval (a, b) such that h(c) = 0, which implies f(c) = g(c).
Why is it important to remember that the entire argument is the answer when using the Intermediate Value Theorem?
-The entire argument is important because it not only provides the answer but also justifies the use of the theorem. It shows the logical steps taken to apply the theorem and how the conclusion was reached, which is essential for understanding and proving mathematical concepts.
Outlines
📚 Introduction to the Intermediate Value Theorem
This paragraph introduces the concept of the Intermediate Value Theorem (IVT). It explains that for a function to apply IVT, it must be continuous on a closed interval, which includes the endpoints. The function values at these endpoints must not be equal, allowing for the existence of a value 'C' between them where the function equals a given 'M'. The IVT is useful for proving the existence of solutions without necessarily finding them. An example is given using two continuous functions, f(X) and g(X), to demonstrate how defining a new function H(X) = f(X) - g(X) and applying IVT can prove that f(X) = g(X) for some X within a given interval.
🔍 Applying IVT to Determine the Number of Zeros
The second paragraph delves into applying the Intermediate Value Theorem to determine the minimum number of times a function equals zero over a given interval. It uses a table of function values to establish that the function changes sign at three points within the interval from 1 to 4. By the IVT, it concludes that the function must cross the x-axis (equal zero) at least three times within the subintervals of 1 to 2, 2 to 3, and 3 to 4. The paragraph emphasizes the importance of writing out the reasoning process when using such theorems, as this forms the complete answer to the problem.
Mindmap
Keywords
💡Intermediate Value Theorem
💡Continuous function
💡Closed interval
💡Endpoints
💡Horizontal line
💡Y-value
💡Open interval
💡Combining functions
💡New function
💡Calculating values
💡Minimum number of times
Highlights
The Intermediate Value Theorem (IVT) is a fundamental principle in calculus that can be used to prove the existence of solutions to certain types of problems.
For IVT to apply, a function f(x) must be continuous on a closed interval [a, b], which includes the endpoints.
The values f(a) and f(b) must not be equal; they can be on different horizontal levels but cannot lie on the same horizontal line.
If f(a) and f(b) have different values, there exists at least one value c within the interval (a, b) such that f(c) equals any given y value between f(a) and f(b).
The value c guaranteed by IVT exists within the open interval (a, b) and not at the endpoints.
IVT is useful for proving the existence of solutions without necessarily providing a method to find them.
An example illustrates the theorem by showing that if f(a) is less than f(b) and a certain y-value M lies between them, there is a horizontal line that intersects the graph at some point c.
A new function H(x) can be defined as f(x) - g(x) to apply IVT when both f(x) and g(x) are continuous functions.
By calculating H(-2) and H(8), one can use IVT to show that H(x) must equal zero for some x between -2 and 8, implying f(x) = g(x) for that x.
IVT can be used to determine the minimum number of times a function equals zero within a given interval by examining the function values at specific points.
The theorem guarantees that if f(x) is continuous and f(1) and f(4) are not zero, f(x) must equal zero at least three times in the interval [1, 4].
The process of applying IVT often involves defining a new function, calculating values at endpoints, and then using the theorem to find the existence of a solution within an interval.
When using IVT, it is important to remember that the value of x that satisfies the condition is only guaranteed to exist within the open interval, not at the endpoints.
The theorem is a powerful tool in calculus that can be applied in various problems, including those that appear on AP Calculus exams.
The video provides a step-by-step approach to using IVT, starting from understanding the conditions required for its application to solving sample problems.
IVT is particularly useful when dealing with functions that are continuous but for which finding explicit solutions is challenging.
The video emphasizes the importance of continuity in applying IVT and how it ensures the existence of a solution within a specified interval.
The presenter demonstrates the application of IVT by solving two different problems, showcasing the versatility of the theorem in calculus.
Understanding and applying IVT is an essential skill for students studying calculus, as it is widely used to establish the existence of solutions to various mathematical problems.
Transcripts
Browse More Related Video
Intermediate Value Theorem
How to show that a solution exists to a functions using IVT

Justification with the intermediate value theorem: table | AP Calculus AB | Khan Academy

Calculus 1 Lecture 3.2: A BRIEF Discussion of Rolle's Theorem and Mean-Value Theorem.

Mean Value Theorem with Example
Intermediate Value Theorem, calculus 1 tutorial, showing a root of a function on an interval
5.0 / 5 (0 votes)
Thanks for rating: