Finding degrees of freedom, critical values, and a standard deviation confidence interval estimate

AspireMtnAcademy

25 May 201906:10

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, Professor Curtis from Aspire Mountain Academy guides viewers through calculating degrees of freedom, critical values, and a confidence interval estimate for the population standard deviation. Using a sample size of 25 with a standard deviation of 0.26 and a 99% confidence level, the video demonstrates how to find these statistics using StatCrunch. The process includes using the chi-square distribution for critical values and adjusting for variance to estimate the standard deviation, with a focus on clarity and application.

Takeaways

📚 The video is a statistics homework help by Professor Curtis from Aspire Mountain Academy.
🔢 The main topic is to find degrees of freedom, critical values, and a confidence interval estimate for the population standard deviation (Sigma).
📉 The assumption is that a simple random sample is selected from a normally distributed population.
🎯 A 99% confidence level is required for the interval estimate.
🔡 The sample size is 25, and the sample standard deviation is 0.26.
🔑 Degrees of freedom are calculated as one less than the sample size, which is 24 in this case.
📊 To find critical values, the chi-square distribution is used with StatCrunch, a statistical software.
📈 The chi-square calculator is accessed for the critical values corresponding to the 99% confidence level.
📐 The critical value on the left (subscript L) and the right (subscript R) are obtained from the calculator.
🧮 For the confidence interval estimate of the population standard deviation, the sample variance is calculated by squaring the sample standard deviation.
📝 The confidence interval for variance is computed in StatCrunch, and then the square root is taken to convert it to the standard deviation interval.
🌐 Aspire Mountain Academy offers more resources for learning statistics, and viewers are encouraged to provide feedback.

Q & A

What is the topic of the video by Professor Curtis from Aspire Mountain Academy?
-The video is about how to find degrees of freedom, critical values, and a confidence interval estimate for the population standard deviation in a statistics homework problem.
What is the sample size given in the problem statement?
-The sample size given in the problem statement is 25.
How is the number of degrees of freedom calculated in this context?
-The number of degrees of freedom is calculated as one less than the sample size, which in this case is 24 (25 - 1).
What statistical software does Professor Curtis use to find critical values?
-Professor Curtis uses StatCrunch to find the critical values.
What type of calculator is accessed in StatCrunch to find the critical values for this problem?
-The Chi-square calculator is accessed in StatCrunch to find the critical values.
What is the confidence level required for the interval in this problem?
-The required confidence level for the interval in this problem is 99%.
How does the video explain the relationship between sample standard deviation and sample variance?
-The video explains that the sample variance can be obtained by squaring the sample standard deviation.
What is the method used in StatCrunch to calculate the confidence interval for standard deviation?
-The method used is to first calculate the confidence interval for variance and then take the square root of the variance to get the confidence interval for standard deviation.
What is the purpose of the video's final remarks about Aspire Mountain Academy?
-The final remarks are an invitation for viewers to visit Aspire Mountain Academy's website for more lecture videos and to provide feedback on what they would like to see in future content.
How does the video script suggest improving one's understanding of statistics?
-The video script suggests that if a viewer's stats teacher is not helpful or engaging, they can visit Aspire Mountain Academy for more accessible and helpful lecture videos.
What is the significance of the critical values in the context of this video?
-The critical values are significant as they are used to define the boundaries of the confidence interval for the population standard deviation.

Outlines

00:00

📚 Introduction to Degrees of Freedom and Confidence Intervals

Professor Curtis from Aspire Mountain Academy introduces the topic of finding degrees of freedom, critical values, and the confidence interval estimate for the population standard deviation. The problem statement outlines the task of using given information to calculate these values, assuming a simple random sample from a normally distributed population. The professor explains that with a 99% confidence level, a sample size of 25, and a sample standard deviation of 0.26, the degrees of freedom are calculated as 24 (one less than the sample size).

05:01

📉 Calculating Critical Values Using StatCrunch

The professor demonstrates how to calculate the critical values required for a 99% confidence interval using StatCrunch. He accesses the chi-square distribution calculator within StatCrunch, inputs the degrees of freedom (24), and the confidence level (99%). The calculator provides two critical values, one for each tail of the distribution. The left critical value is identified as the primary value needed for the next steps, and the professor rounds it to three decimal places for accuracy.

🔍 Confidence Interval Estimate for Population Standard Deviation

To estimate the population standard deviation with a 99% confidence interval, the professor returns to StatCrunch and uses the 'stat variant stats' function, entering the squared sample standard deviation as the sample variance. With the sample size and confidence level set, the calculator provides the interval for the variance. The professor then takes the square root of these values to convert the interval estimate from variance to standard deviation, providing the final lower and upper limits for the confidence interval.

Mindmap

Keywords

💡Degrees of Freedom

Degrees of freedom refers to the number of independent values in a set of data that can vary freely. In the context of the video, it is calculated as one less than the sample size, which is 25, making it 24. This concept is crucial for understanding statistical tests, as it affects the distribution of the test statistic, particularly in the chi-squared distribution used to find critical values.

💡Critical Values

Critical values are the threshold values in a statistical test that determine the acceptance or rejection of a null hypothesis. The video demonstrates how to find these values using the chi-squared distribution for a 99% confidence level, which are essential for constructing confidence intervals and making statistical inferences about the population parameter.

💡Confidence Interval

A confidence interval is a range of values, derived from a statistical model, that is likely to contain the value of an unknown population parameter. The video focuses on calculating the 99% confidence interval estimate for the population standard deviation, which provides a measure of the precision of the sample standard deviation estimate.

💡Population Standard Deviation (Sigma)

Sigma, often represented by the Greek letter σ, is the standard deviation of the entire population. In the video, the task is to estimate this value using the sample standard deviation and the calculated confidence interval, which is a fundamental concept in inferential statistics.

💡Sample Size

Sample size is the number of observations or elements in a sample used for statistical analysis. In the script, a sample size of 25 is given, which is used to calculate degrees of freedom and is a key factor in determining the precision of the confidence interval.

💡Sample Standard Deviation

The sample standard deviation is a measure of the amount of variation or dispersion in a set of data values. In the video, a sample standard deviation of 0.26 is provided, which is then used to calculate the sample variance and subsequently the confidence interval for the population standard deviation.

💡Chi-Squared Distribution

The chi-squared distribution is a probability distribution used in statistical tests where the test statistic is a sum of the squares of k independent standard normal random variables. The video uses the chi-squared calculator in StatCrunch to find the critical values needed for the confidence interval.

💡StatCrunch

StatCrunch is a statistical software application used for data analysis. The video script describes using StatCrunch to calculate critical values and confidence intervals, demonstrating its utility in performing complex statistical calculations.

💡Variance

Variance is a measure of the dispersion of a set of data points around their mean value. In the video, the variance is calculated by squaring the sample standard deviation, which is then used to find the confidence interval for the population standard deviation.

💡99% Confidence Level

The 99% confidence level indicates the level of confidence that the calculated confidence interval will contain the true population parameter. The video script uses this level to determine the critical values and the confidence interval for the population standard deviation.

💡Square Root

In the context of the video, the square root is used to convert the confidence interval of variance to the confidence interval of standard deviation. This mathematical operation is essential for obtaining the final interval estimate in the correct units.

Highlights

Introduction to finding degrees of freedom, critical values, and confidence interval estimate for standard deviation.

Assumption of a simple random sample from a normally distributed population.

The requirement of a 99% confidence level for the interval.

Sample size of 25 and sample standard deviation of 0.26 provided.

Calculation of degrees of freedom as one less than the sample size.

Use of StatCrunch for finding critical values.

Accessing the chi-square distribution in StatCrunch for critical value calculation.

Entering the degrees of freedom and confidence level into StatCrunch.

Obtaining the critical values for the chi-square distribution.

Calculation of the left critical value for the confidence interval.

Calculation of the right critical value for the confidence interval.

Using StatCrunch to calculate the confidence interval for the population standard deviation.

Understanding that variance is the square of the standard deviation.

Entering the squared sample standard deviation as the sample variance in StatCrunch.

Setting up the confidence interval calculation in StatCrunch.

Computing the lower and upper limits of the confidence interval for variance.

Converting the confidence interval from variance to standard deviation by taking the square root.

Finalizing the confidence interval estimate for the population standard deviation.

Encouragement for feedback and further learning through Aspire Mountain Academy.

Transcripts

Browse More Related Video

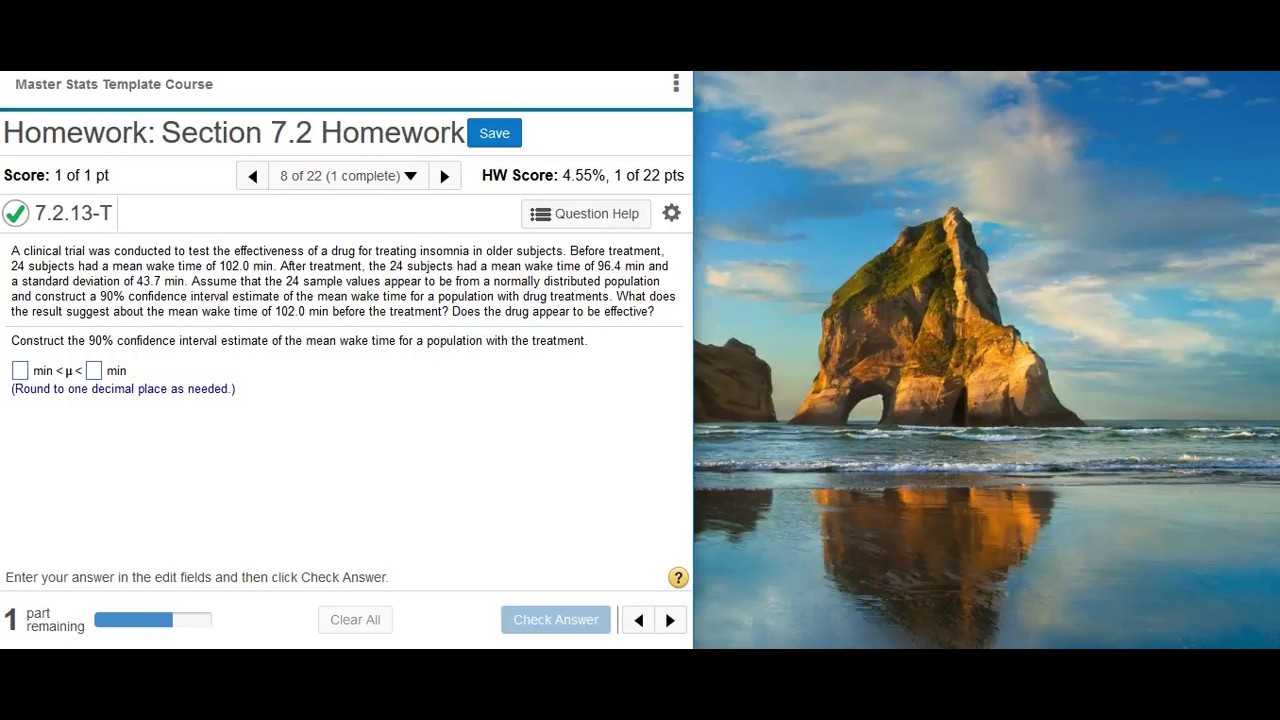
Finding and interpreting a confidence interval for a population mean (σ unknown)

Confidence Intervals | Population Mean: σ Unknown

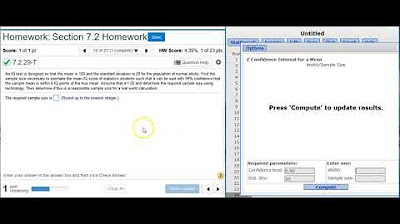
Finding the sample size needed to estimate a confidence interval on a population mean

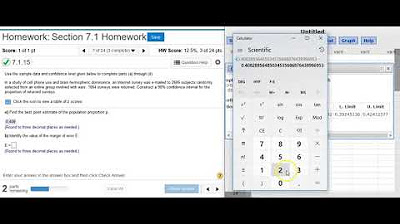
Finding the best point estimate and confidence interval for proportions

7.1.3 Estimating a Population Proportion - Critical Values, Rationale and How to Compute Them

[6.4.6-T] Finding probabilities for different sample sizes using a nonstandard normal distribution

Finding degrees of freedom, critical values, and a standard deviation confidence interval estimate

Takeaways

Q & A

What is the topic of the video by Professor Curtis from Aspire Mountain Academy?

What is the sample size given in the problem statement?

How is the number of degrees of freedom calculated in this context?

What statistical software does Professor Curtis use to find critical values?

What type of calculator is accessed in StatCrunch to find the critical values for this problem?

What is the confidence level required for the interval in this problem?

How does the video explain the relationship between sample standard deviation and sample variance?

What is the method used in StatCrunch to calculate the confidence interval for standard deviation?

What is the purpose of the video's final remarks about Aspire Mountain Academy?

How does the video script suggest improving one's understanding of statistics?

What is the significance of the critical values in the context of this video?