[6.4.6-T] Finding probabilities for different sample sizes using a nonstandard normal distribution

AspireMtnAcademy
15 Mar 201807:33
EducationalLearning
32 Likes 10 Comments

TLDRIn this Aspire Mountain Academy video, Professor Curtis offers a step-by-step guide on calculating probabilities for nonstandard normal distributions. He demonstrates using StatCrunch to find the probability of an individual's overhead reach exceeding 212.5 cm and adjusts the standard deviation for a sample mean exceeding 198.2 cm with a sample size of 20. Curtis emphasizes the Central Limit Theorem's flexibility in applying to normally distributed data regardless of sample size, providing clarity on its use in the context of the problem.

Takeaways
  • 📚 Professor Curtis from Aspire Mountain Academy is providing statistics homework help on finding probabilities with a nonstandard normal distribution.
  • 📊 The problem involves the overhead reach distances of adult females, which are normally distributed with a mean of 200 cm and a standard deviation of 8 cm.
  • 🔍 Part A of the problem asks to find the probability of an individual distance being greater than 212.5 cm, which can be calculated using the Normal calculator in StatCrunch.
  • 📝 Adjusting the mean and standard deviation in the Normal calculator is necessary to reflect the nonstandard normal distribution given in the problem statement.
  • 👉 In the Normal calculator, selecting 'greater than' and entering 212.5 cm will compute the desired probability, which should be rounded to four decimal places.
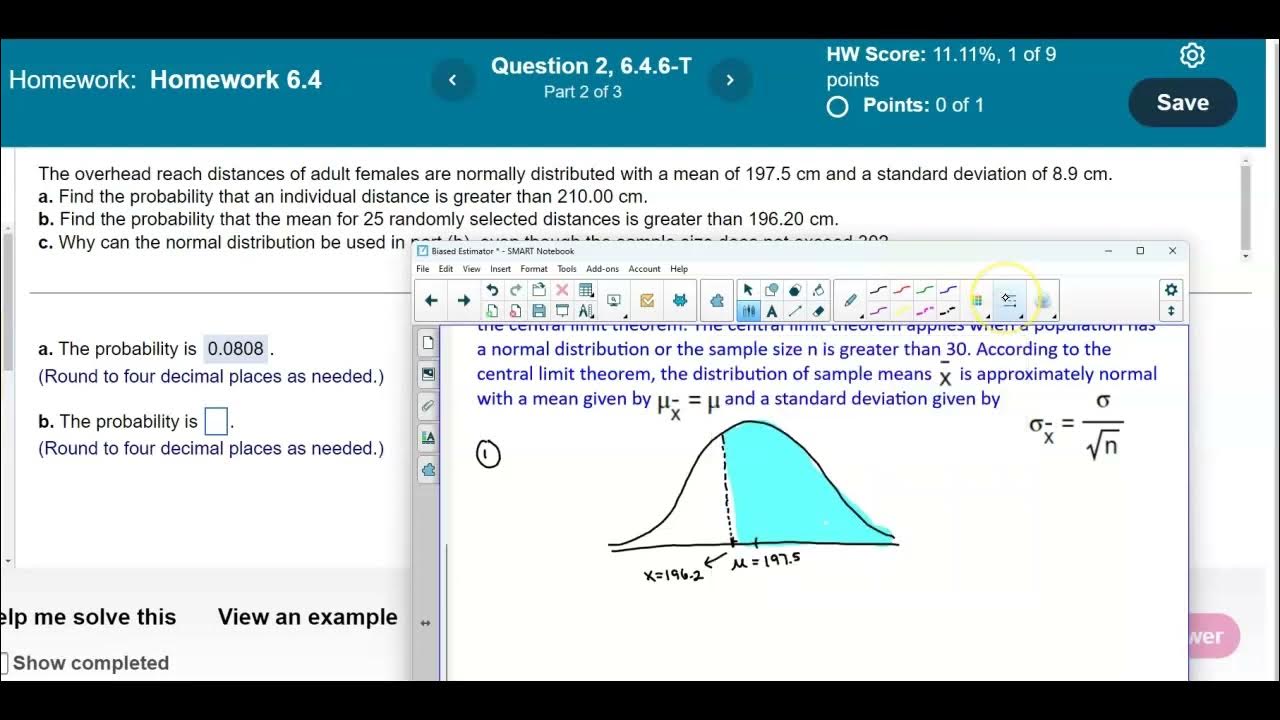
  • 🔄 Part B requires finding the probability that the mean of 20 randomly selected distances is greater than 198.2 cm, which involves an adjustment to the standard deviation.
  • 📐 The adjustment for Part B is calculated by dividing the population standard deviation by the square root of the sample size (20 in this case), resulting in a new standard deviation for the sample mean.
  • 💻 To avoid rounding errors, it's recommended to calculate the adjusted standard deviation using a computer calculator and then input it into StatCrunch.
  • 🔢 After adjusting the standard deviation and entering the new random variable value of 198.2 cm, the Normal calculator will compute the probability for the sample mean.
  • 📚 Part C discusses the use of the normal distribution in Part B, even with a sample size less than 30, referencing the Central Limit Theorem and the fact that the data is already normally distributed.
  • 🎯 The Central Limit Theorem allows for the assumption of normality for the sample mean if the sample size is large enough, but it's not a requirement if the data is already normally distributed.
  • 📝 Answer Option B is selected as the correct answer for Part C, emphasizing that the data's normal distribution is the reason for using the normal distribution in the problem.
Q & A

  • What is the topic of the video by Professor Curtis?

    -The video is about finding probabilities for different sample sizes using a nonstandard normal distribution in the context of statistics homework help.

  • What is the mean and standard deviation of the adult females' overhead reach distances mentioned in the video?

    -The mean of the overhead reach distances is 200 centimeters, and the standard deviation is 8 centimeters.

  • What is the probability calculation for Part A of the problem statement?

    -Part A asks for the probability that an individual distance is greater than 212.5 cm, which is calculated using the normal distribution with the given mean and standard deviation.

  • Why does Professor Curtis use the Normal calculator in StatCrunch for the problem?

    -The Normal calculator is used because the data are normally distributed, and it allows for the adjustment of mean and standard deviation to fit the nonstandard normal distribution given in the problem statement.

  • How does StatCrunch calculate the probability for an individual distance greater than a certain value?

    -StatCrunch calculates the probability by setting the 'greater than' condition in the calculator and inputting the specific value, which in this case is 212.5 cm.

  • What adjustment is needed for the standard deviation when calculating the probability in Part B of the problem?

    -For Part B, the standard deviation needs to be divided by the square root of the sample size to adjust for the sample mean of a larger sample.

  • Why is the sample size adjustment necessary when calculating the mean of 20 randomly selected distances?

    -The adjustment is necessary because when dealing with a sample size greater than 1, the variability of the sample mean is reduced, which is accounted for by dividing the population standard deviation by the square root of the sample size.

  • What is the Central Limit Theorem and how does it relate to Part B of the problem?

    -The Central Limit Theorem states that if the sample size is greater than 30, the sampling distribution of the sample mean will be approximately normally distributed. However, in this case, the data are already normally distributed, so there is no need for this assumption.

  • Why can the normal distribution be used in Part B even though the sample size is 20, which does not exceed 30?

    -The normal distribution can be used because the data are already normally distributed, as stated in the problem. The Central Limit Theorem's sample size condition is not a requirement when the original distribution is already normal.

  • What is the significance of rounding the standard deviation to four decimal places before inputting it into StatCrunch?

    -Rounding to four decimal places ensures precision in the calculation, avoiding potential discrepancies that could occur from rounding within the calculator itself, which might lead to incorrect results.

  • What is the final step in solving Part B of the problem after adjusting the standard deviation?

    -The final step is to input the adjusted standard deviation into StatCrunch, set the condition for the mean of 20 randomly selected distances to be greater than 198.2 cm, and compute the probability.

  • What is the purpose of the Aspire Mountain Academy mentioned in the video?

    -Aspire Mountain Academy provides additional resources such as lecture videos and homework help for students, especially in statistics, to enhance their learning experience and understanding.

Outlines
00:00
📚 Calculating Individual Probabilities with Nonstandard Normal Distribution

Professor Curtis introduces a statistics homework help video focused on finding probabilities for different sample sizes using a nonstandard normal distribution. He presents a problem involving the overhead reach distances of adult females, which are normally distributed with a mean of 200 cm and a standard deviation of 8 cm. The task is to find the probability that an individual distance exceeds 212.5 cm. The solution involves using StatCrunch's Normal calculator, adjusting the mean and standard deviation from the standard normal distribution to match the problem's nonstandard distribution, and computing the probability for the specified value. The result should be rounded to four decimal places.

05:06
🔍 Adjusting Standard Deviation for Sample Mean Probabilities

In the second part of the video, Professor Curtis addresses how to find the probability that the mean of 20 randomly selected distances is greater than 198.2 cm. He explains the need to adjust the standard deviation for a sample size greater than one, by dividing the population standard deviation by the square root of the sample size. Curtis demonstrates the calculation, ensuring precision by copying the exact value from a computer calculator into StatCrunch. He then inputs this adjusted standard deviation into the Normal calculator, sets the random variable value, and computes the probability, rounding it to four decimal places.

📘 Understanding the Central Limit Theorem in Nonstandard Normal Distributions

The final part of the script discusses why the normal distribution can be used in the previous calculation even though the sample size does not exceed 30, referencing the Central Limit Theorem. Curtis clarifies that while the theorem suggests a sample size greater than 30 for assuming normal distribution, it is not necessary when the data is already normally distributed. He concludes by selecting the correct answer option based on this understanding and encourages viewers to provide feedback or access more resources at Aspire Mountain Academy's website.

Mindmap
Keywords
💡Normal Distribution
Normal distribution, also known as Gaussian distribution, is a continuous probability distribution that is symmetric about the mean, showing the classic bell curve shape. In the video, the normal distribution is the basis for the statistical problems presented, as the overhead reach distances of adult females are described as being normally distributed with a mean of 200 cm and a standard deviation of 8 cm.
💡Sample Size
Sample size refers to the number of observations or elements in a sample used for a particular statistical study. In the context of the video, the sample size is crucial for adjusting the standard deviation when calculating probabilities for a sample mean, as seen in Part B where 20 randomly selected distances are considered.
💡Standard Deviation
Standard deviation is a measure of the amount of variation or dispersion in a set of values. In the video, the standard deviation of 8 cm for the overhead reach distances is used to calculate probabilities and is adjusted when considering the mean of a sample, as per the rules of the Central Limit Theorem.
💡Mean
The mean, often referred to as the average, is the sum of all values in a dataset divided by the number of values. In the video, the mean of 200 cm for the overhead reach distances is a central value around which the data is distributed, and the mean of a sample of 20 is used to find a probability in Part B.
💡Probability
Probability is a measure of the likelihood that a given event will occur. The video discusses finding probabilities for events related to the normal distribution of the overhead reach distances, such as the probability that an individual distance is greater than 212.5 cm.
💡StatCrunch
StatCrunch is a statistical software tool used for data analysis and graphics. In the video, StatCrunch is utilized to calculate probabilities for the normal distribution, demonstrating how to adjust for nonstandard distributions and compute probabilities for specific events.
💡Central Limit Theorem
The Central Limit Theorem is a statistical theory that states that the distribution of sample means approximates a normal distribution as the sample size gets larger, regardless of the shape of the population distribution. The video refers to this theorem to explain why the normal distribution can be used even when the sample size does not exceed 30.
💡Random Variable
A random variable is a variable whose values are determined by outcomes of a random phenomenon. In the video, the random variable could represent an individual's overhead reach distance or the mean of a sample of such distances, which are used to calculate probabilities.
💡Confidence Interval
Although not explicitly mentioned in the video, the concept of a confidence interval is related to the adjustments made to the standard deviation when calculating probabilities for a sample mean. A confidence interval provides a range that is likely to contain the population parameter with a certain level of confidence.
💡Calculation Adjustment
Calculation adjustment refers to the process of modifying the standard deviation when calculating probabilities for a sample mean, as shown in the video. This adjustment involves dividing the population standard deviation by the square root of the sample size to account for the reduced variability in the sample mean compared to individual observations.
💡Rounding
Rounding is the process of adjusting a number to a specified number of decimal places. In the video, rounding is mentioned as a step in ensuring that the probabilities calculated in StatCrunch are presented with the required precision, which is four decimal places in this case.
Highlights

Introduction to finding probabilities for different sample sizes using a nonstandard normal distribution.

Problem statement: Adult females' overhead reach distances are normally distributed with a mean of 200 cm and a standard deviation of 8 cm.

Part A of the problem asks for the probability of an individual distance being greater than 212.5 cm.

Using StatCrunch to tackle the problem with a nonstandard normal distribution.

Adjusting the mean and standard deviation in the Normal calculator to match the problem statement.

Understanding the probability calculation as an area under the curve in the Normal calculator.

Computing the probability for an individual distance greater than 212.5 cm in StatCrunch.

Part B of the problem involves finding the probability that the mean of 20 randomly selected distances is greater than 198.2 cm.

Adjusting the standard deviation for a sample size greater than 1 using the population standard deviation and the square root of the sample size.

Avoiding rounding errors by using a computer calculator for the standard deviation adjustment.

Copying the precise standard deviation value into StatCrunch to avoid rounding errors.

Calculating the probability for the mean of 20 distances being greater than 198.2 cm in StatCrunch.

Rounding the probability to four decimal places for accuracy.

Part C discusses the use of the normal distribution in Part B despite the sample size not exceeding 30.

Explanation of the Central Limit Theorem and its relation to sample size and normal distribution.

Clarification that the normal distribution can be used because the data is already normally distributed, not due to the sample size.

Selecting the correct answer option for Part C based on the normal distribution being stated in the problem.

Encouragement for feedback and further learning at Aspire Mountain Academy.

Invitation to access lecture videos or provide feedback on Aspire Mountain Academy's website.

Transcripts

Browse More Related Video

Finding the sample size needed to estimate a confidence interval on a population mean

Math 14 HW 6.4.6-T Using the Central Limit Theorem

Finding a confidence interval given summary sample data

Finding degrees of freedom, critical values, and a standard deviation confidence interval estimate

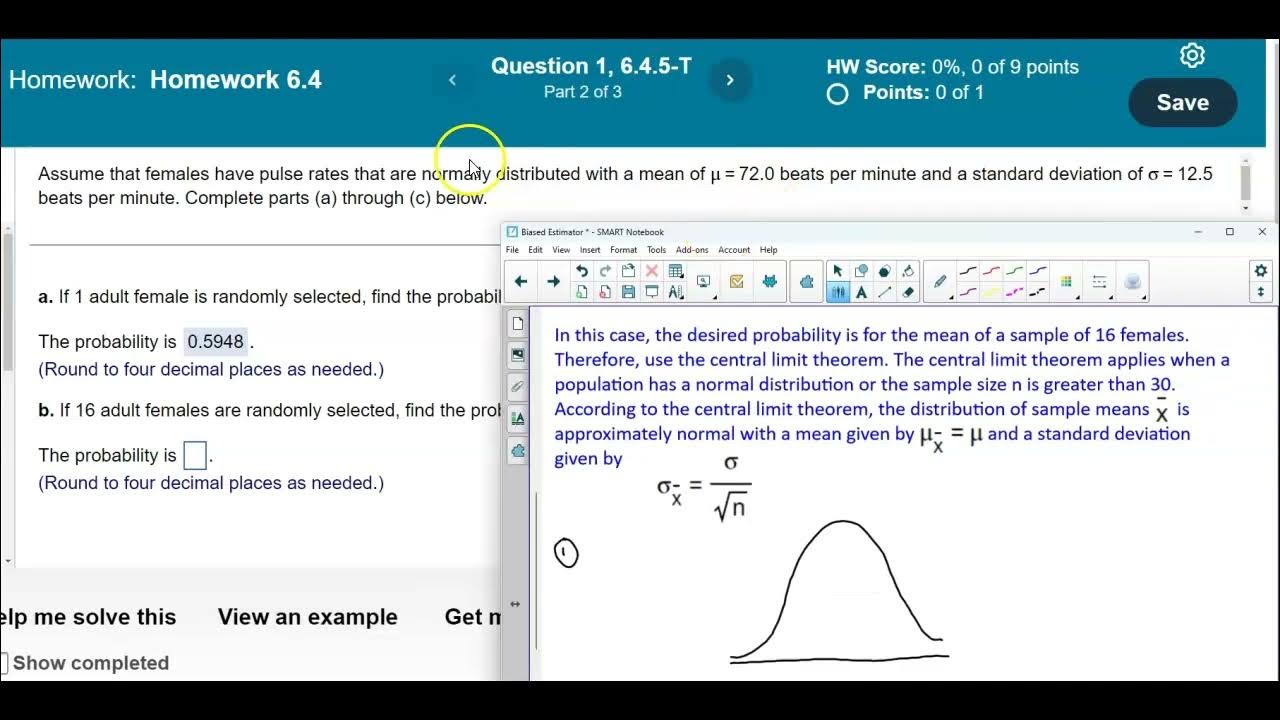
Math 14 HW 6.4.5-T Using the Central Limit Theorem

Finding the best point estimate and confidence interval for proportions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
StatisticsNormal DistributionProbabilitiesSample SizeCentral Limit TheoremEducationAspire Mountain AcademyStatCrunchCalculusData AnalysisAcademic Help