Math 119 Chap 6 part 3
TLDRThis educational video script covers the concept of normal distribution and its applications in statistics. It explains how to find quartiles, use the central limit theorem, and calculate probabilities for various scenarios, such as SAT scores, cholesterol levels, and body temperatures. The script also discusses the sampling distribution of the mean and how it can be approximated as normal, even for skewed populations, given a large enough sample size. The use of calculator functions like inverse norm and normal cdf is highlighted for solving these statistical problems.
Takeaways
- 📚 The lecture focuses on Chapter 6, specifically on statistical concepts related to normal distribution, quartiles, and z-scores.
- 📈 The importance of understanding quartiles as dividing the data into 25% increments is emphasized, especially in the context of normal distribution.
- 📊 The use of visual aids like drawing the normal distribution curve is highlighted to help students keep track of calculations and concepts.
- 🧮 The video demonstrates how to calculate the first quartile using the inverse norm function on a calculator, given the mean and standard deviation.
- 🔢 An example is provided to find the first quartile for 14-year-old boys' cholesterol levels, using the normal distribution properties.
- 🤔 The script discusses the process of 'unstandardizing' a z-score back to the original units of measurement using a specific formula.
- 📘 The SAT scores example is used to illustrate how to find the score that places a student in the top 5%, using the inverse norm function.
- 🚶♂️ The weights of adult men are described as normally distributed, and the script shows how to calculate the heaviest and lightest cutoffs for certain percentiles.
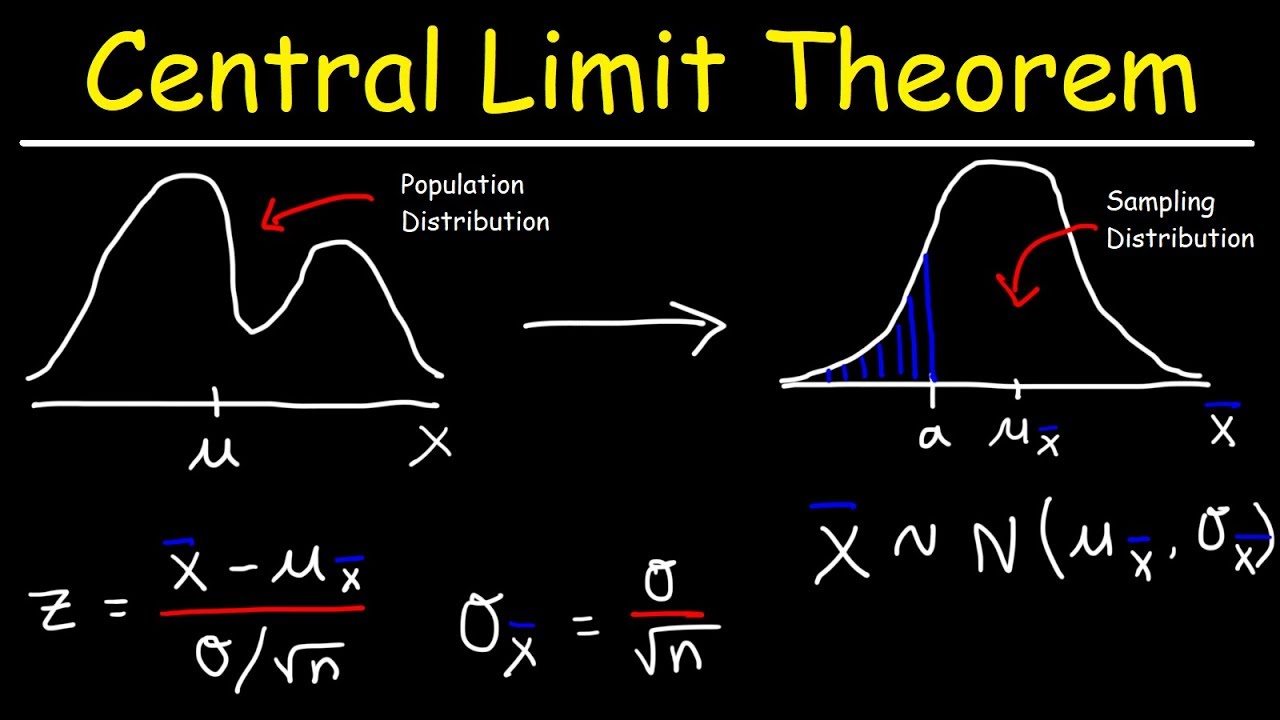
- 🔑 The Central Limit Theorem is explained, stating that the distribution of sample means will be approximately normal if the sample size is large enough, regardless of the original distribution.
- 🏢 An application of the Central Limit Theorem is shown with an example of apartment rental prices in San Diego, explaining the sampling distribution of the sample mean.
- 🤒 The script concludes with a discussion on body temperature distributions, emphasizing the use of the Central Limit Theorem to handle non-normal distributions when sample sizes are large.
Q & A
What is the main topic of the video script?
-The main topic of the video script is the explanation of statistical concepts related to normal distribution, quartiles, z-scores, and the central limit theorem, using various examples including cholesterol levels, SAT scores, rental prices, and body temperatures.
What is the significance of the first quartile in the context of the video?
-The first quartile is significant as it represents the 25th percentile of a dataset, which means that 25% of the data falls below this value. The video explains how to calculate the first quartile using a normal distribution curve and a calculator.
How does the video script explain the process of finding the z-score corresponding to a given proportion?
-The video script explains that to find the z-score corresponding to a given proportion, one should use the inverse norm function on a calculator, taking into account the mean and standard deviation of the distribution.
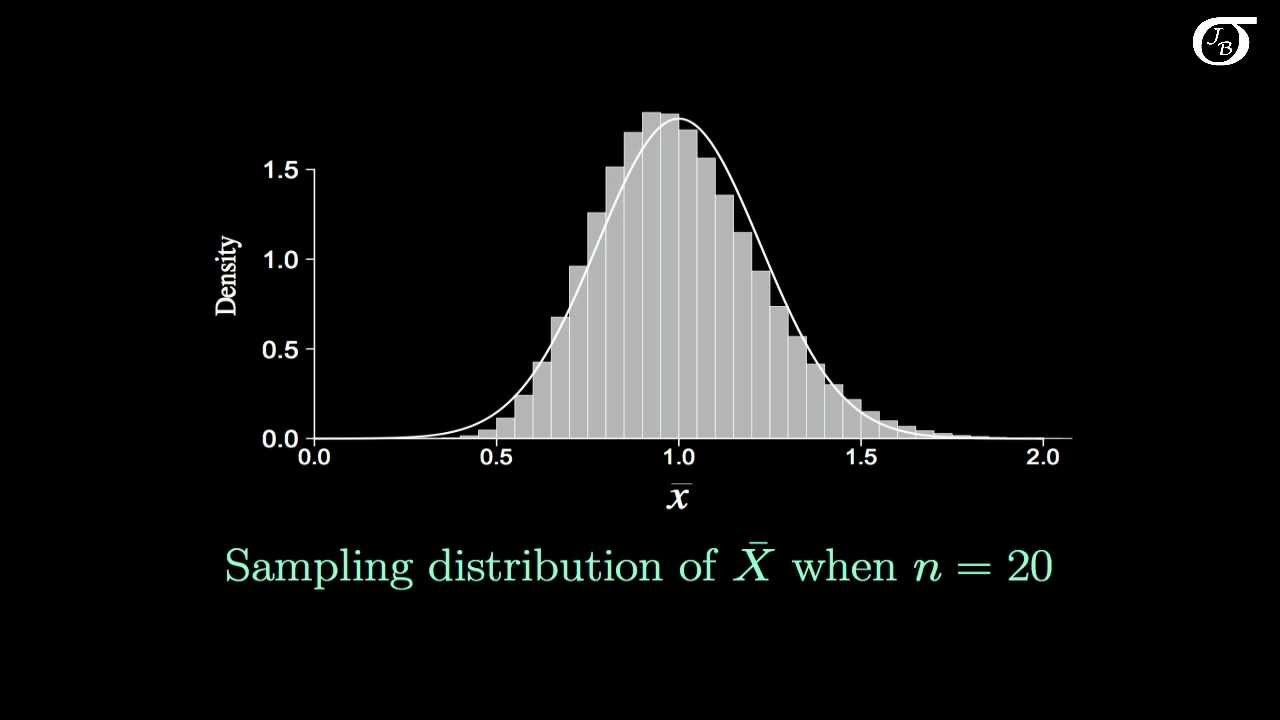
What is the central limit theorem and how is it demonstrated in the video?
-The central limit theorem states that the distribution of sample means will be approximately normal if the sample size is large enough, regardless of the shape of the population distribution. The video demonstrates this with an animation showing how the means of various samples from a non-normal distribution become normally distributed as more samples are taken.
How does the video script use the example of SAT scores to illustrate a statistical concept?
-The video script uses the example of SAT scores to illustrate how to find the score that places a student in the top five percent. It explains the process of using the inverse norm function with the given mean and standard deviation to find the specific SAT score.
What is the importance of knowing the mean and standard deviation when working with normal distributions?
-Knowing the mean and standard deviation is crucial when working with normal distributions because these values allow for the calculation of probabilities, percentiles, and z-scores, which are essential for statistical analysis and inference.
How does the video script explain the concept of unstandardizing a z-score?
-The video script explains the concept of unstandardizing a z-score by showing how to convert a z-score back into the original units of the data using the formula x = z * standard deviation + mean.
What is the purpose of drawing a picture when calculating quartiles or other statistical measures?
-Drawing a picture helps to visualize the distribution and understand the proportion of data that falls below or above certain values. It helps to avoid confusion and ensures that the correct calculations are being performed.
How does the video script address the concept of probability in relation to the top and bottom percentiles?
-The video script addresses the concept of probability by showing how to calculate the scores or values that correspond to specific percentiles, such as the top five percent or the bottom ten percent, using the inverse norm function and the properties of normal distribution.
What is the practical application of understanding the central limit theorem in real-world scenarios?
-Understanding the central limit theorem is important in real-world scenarios because it allows for making inferences about population parameters based on sample data. It is particularly useful in quality control, economics, social sciences, and any field where averages of samples are used to estimate population characteristics.
Outlines
📚 Chapter 6 IQ Scores and Cholesterol Distribution
The instructor discusses the completion of Chapter 6, focusing on IQ scores and cholesterol levels in 14-year-old boys. They explain the concept of quartiles and how to use the normal distribution to find the first quartile of cholesterol levels, given the mean and standard deviation. The process involves drawing a picture to visualize the distribution, using the normal cumulative distribution function (CDF), and calculating the inverse norm to find the z-score corresponding to the 25th percentile. The instructor emphasizes the importance of understanding the process rather than just using the calculator.
📉 SAT Scores and Z-Score Calculation
The video script moves on to discuss SAT scores, which are normally distributed with a mean of 504 and a standard deviation of 111. The task is to determine the score needed to be in the top five percent. The instructor uses the inverse norm function on a calculator to find the z-score that corresponds to the top five percent, which is not directly available from the calculator due to its left-to-right calculation direction. After finding the z-score, the score of 686.579 is calculated as the threshold for the top five percent. The process of unstandardizing the z-score using the formula is also demonstrated.
🏋️♂️ Weight Distributions in Adult Men and the Central Limit Theorem
The script covers the weights of adult men, which are normally distributed with a mean of 172 and a standard deviation of 29. The task is to find the weight that represents the heaviest 0.5 percent of men. The instructor uses the inverse norm function again, this time with a probability of 0.995 to find the cutoff weight for the heaviest 0.5 percent. The concept of the central limit theorem is introduced with an animation, illustrating how the distribution of sample means from a non-normal population can become normal as the sample size increases.
📊 Understanding the Central Limit Theorem with Sample Means
The instructor delves deeper into the central limit theorem, explaining that the distribution of sample means from any population will be approximately normal if the sample size is large enough (n > 30). They clarify that while the original population distribution does not have to be normal, the distribution of the sample means will be. The standard deviation of the sample means is shown to be the original standard deviation divided by the square root of the sample size, n.
🏢 Application of the Central Limit Theorem in Apartment Rent Prices
The script applies the central limit theorem to the rent prices of apartments in San Diego, which follow a skewed distribution with a mean of 715 and a standard deviation of 135. The task is to describe the sampling distribution of the sample mean rental price for 75 apartments. The instructor demonstrates that even though the original distribution is skewed, the sampling distribution of the mean can be treated as normal due to the central limit theorem, with a mean of 715 and a standard deviation of 135 divided by the square root of 75.
🚶♂️ Probability of Exceeding Weight Limits with a Sample of Men
The script discusses the probability that the average weight of a sample of 18 men exceeds the weight limit for an elevator, which is set at 3,500 pounds in total. The men's weights are normally distributed with a mean of 175 pounds and a standard deviation of 25. The instructor calculates the probability using the normal CDF function with the adjusted standard deviation for the sample mean and finds a very small probability of the event occurring, indicating it is highly unlikely for 18 men to exceed the weight limit on average.
🌡️ Body Temperature Distribution and Probability of a Sample Mean
The final paragraph discusses the distribution of human body temperatures, which are assumed to have a mean of 98.6 degrees Fahrenheit and a standard deviation of 0.62. With a sample size of 106 people, the instructor calculates the probability that the average body temperature of the sample is 98.2 or lower. The use of the central limit theorem allows the application of the normal distribution to find this probability, which is found to be extremely low, suggesting that it is rare for the average body temperature of a large sample to be below the commonly accepted mean.
Mindmap
Keywords
💡Quartiles
💡Normal Distribution
💡Standard Deviation
💡Mean
💡Inverse Norm
💡Z-Score
💡Central Limit Theorem
💡Sampling Distribution
💡Normal CDF Function
💡Body Temperature
Highlights
Introduction to Chapter 6, focusing on IQ scores and test questions.
Explanation of quartiles and their significance in statistical analysis.
Utilization of the normal distribution to find the first quartile of cholesterol levels in 14-year-old boys.
Instruction on using calculator functions for inverse norm calculations.
Clarification on how to interpret and use z-scores in statistical problems.
Demonstration of unstandardizing a z-score back to the original scale.
Application of normal distribution to SAT scores to determine percentiles.
Method to calculate the top and bottom percentiles using inverse norm.
Discussion on the central limit theorem and its implications for sample means.
Illustration of how sample means from non-normal distributions can approximate a normal distribution.
Explanation of how to calculate the standard deviation of a sampling distribution of the mean.
Analysis of the probability of a single 12th grader scoring above a certain threshold on a math test.
Calculation of the probability for a sample mean of 12th graders' scores exceeding a value.
Description of the sampling distribution of apartment rental prices in San Diego.
Probability calculation for the average rental price in a sample exceeding a certain value.
Application of the central limit theorem to the weights of men and the weight limit of an elevator.
Probability assessment of the average weight of 18 men exceeding an elevator's weight limit.
Final problem involving body temperature distributions and the probability of a sample mean being below a certain value.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: