Introduction to the Central Limit Theorem

jbstatistics
28 Dec 201213:13
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the Central Limit Theorem (CLT), a pivotal statistical concept illustrating how the distribution of sample means approaches normality as sample size increases, irrespective of the original population distribution. Through simulations, it demonstrates the CLT's application with different distributions, showing how a sample size of at least 30 generally ensures normality of the sample mean. The script also highlights the CLT's significance in enabling the use of normal distribution-based statistical methods, even with non-normal populations, and illustrates its utility in probability calculations, such as estimating the likelihood of an average salary exceeding a certain threshold in a large corporation.

Takeaways
  • ๐Ÿ“š The Central Limit Theorem (CLT) is a fundamental concept in statistics, stating that the distribution of sample means will approach a normal distribution as the sample size increases, regardless of the population distribution.
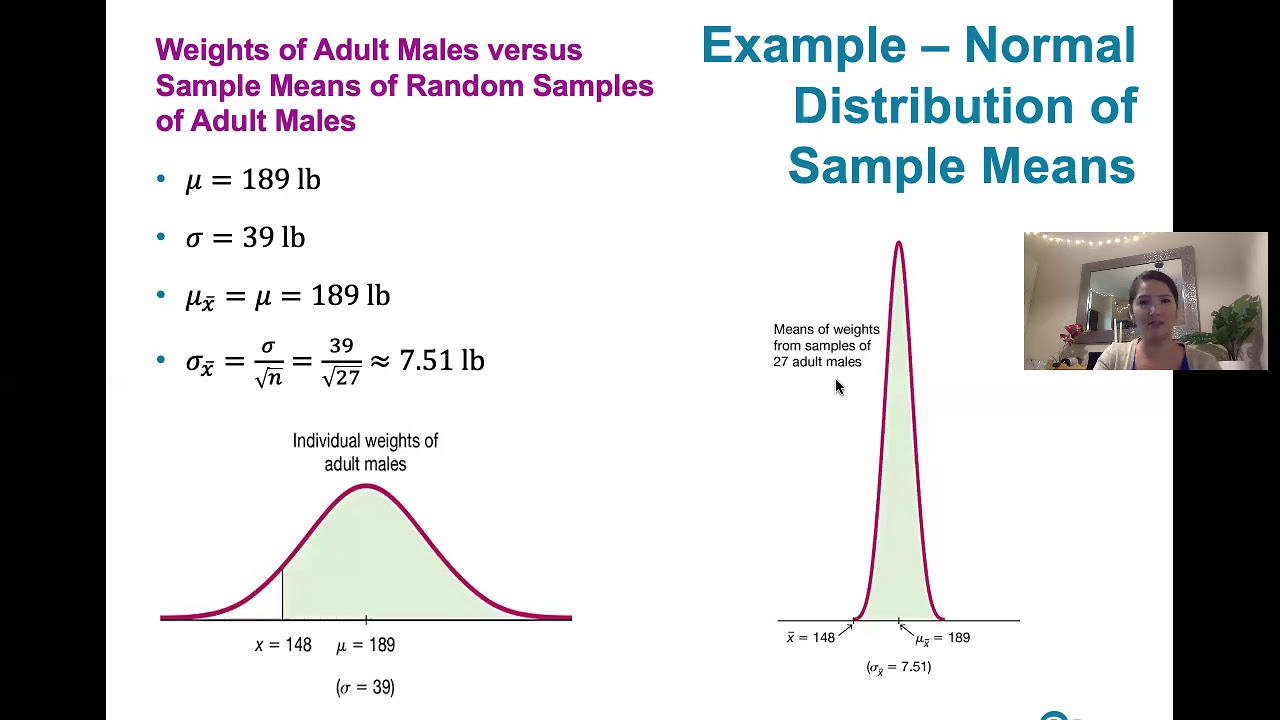
  • ๐Ÿ“Š The mean of the sampling distribution of the sample mean (Xฬ„) is equal to the population mean (ฮผ), and the standard deviation of this distribution is the population standard deviation (ฯƒ) divided by the square root of the sample size (n).
  • ๐Ÿ’ก If the population is normally distributed, the sample mean (Xฬ„) is also normally distributed. The CLT extends this to non-normal populations by stating that the sample mean will tend toward a normal distribution as n increases.
  • โš–๏ธ The CLT allows for the use of normal distribution-based statistical inference and probability calculations even when sampling from non-normal populations, provided the sample size is large enough.
  • ๐Ÿ“ˆ A rough guideline is that the sample mean can be considered approximately normally distributed if the sample size is at least 30, although this can vary depending on the specific context.
  • ๐Ÿ” Through simulation, it's demonstrated that as the sample size increases, the distribution of sample means becomes increasingly closer to a normal distribution, even for non-normal populations like exponential or mixed distributions.
  • ๐Ÿ“‰ The shape of the distribution of sample means changes as the sample size increases, with skewness reducing and the distribution becoming more symmetrically normal.
  • ๐Ÿงฎ Technically, the CLT requires that the population mean and variance be finite, which is typically the case for most practical applications.
  • ๐Ÿค” The CLT is particularly useful for probability calculations involving sample means, allowing for the estimation of probabilities even when the underlying population distribution is unknown or non-normal.
  • ๐Ÿ’ผ In practical scenarios, such as calculating the probability of an average salary exceeding a certain threshold in a large corporation, the CLT provides a method to estimate probabilities using a standardized normal distribution.
  • ๐ŸŒŸ The CLT is a powerful tool in statistics, enabling the application of normal distribution-based methods in a wide range of situations, and greatly simplifies the process of statistical analysis.
Q & A

  • What is the central limit theorem?

    -The central limit theorem is a statistical concept stating that the distribution of the sample mean tends toward a normal distribution as the sample size increases, regardless of the original distribution from which the samples are drawn.

  • Why is the central limit theorem important in statistics?

    -The central limit theorem is important because it allows us to use normal distribution-based statistical inference procedures and probability calculations even when we are sampling from populations that are not normally distributed, provided we have a sufficiently large sample size.

  • What are the characteristics of the sampling distribution of the sample mean?

    -The sampling distribution of the sample mean, represented by X bar, has a mean equal to the population mean (mu) and a standard deviation equal to sigma over the square root of the sample size (n).

  • How does the central limit theorem apply to non-normal populations?

    -According to the central limit theorem, even if the population is not normally distributed, the distribution of the sample mean will approach a normal distribution as the sample size increases.

  • What is the rough guideline for considering the sample mean to be approximately normally distributed?

    -As a rough guideline, the sample mean can be considered to be approximately normally distributed if the sample size is at least 30.

  • How does the central limit theorem help in probability calculations?

    -The central limit theorem allows us to approximate probabilities for the sample mean using the standard normal distribution, even when the underlying population distribution is unknown or non-normal, as long as the sample size is large enough.

  • What is the role of the sample size in the central limit theorem?

    -The sample size plays a crucial role in the central limit theorem, as it determines how closely the distribution of the sample mean approximates a normal distribution. Larger sample sizes result in a more normal distribution of the sample mean.

  • Can the central limit theorem be applied to any distribution, even if it is highly skewed or has outliers?

    -While the central limit theorem is generally robust, it is more applicable to distributions that are not extremely skewed or have too many outliers. However, for large enough sample sizes, the theorem can still provide a reasonable approximation to a normal distribution.

  • What is the technical restriction mentioned in the script regarding the application of the central limit theorem?

    -The technical restrictions for applying the central limit theorem include the requirement that the mean and variance of the population must be finite.

  • How does the central limit theorem assist in making statistical inferences about a population from a sample?

    -The central limit theorem allows us to make statistical inferences about a population's mean from a sample mean, even if the population distribution is unknown, by providing a way to approximate the distribution of the sample mean as normal for large sample sizes.

  • Can you provide an example of how the central limit theorem is used in a practical scenario?

    -In the script, an example is given where salaries at a large corporation have a mean of $62,000 and a standard deviation of $32,000. Using the central limit theorem, we can approximate the probability that the average salary of a randomly selected group of 100 employees exceeds $66,000, even though individual salaries may not follow a normal distribution.

Outlines
00:00
๐Ÿ“š Introduction to the Central Limit Theorem

The video script begins by introducing the Central Limit Theorem (CLT), a fundamental concept in statistics. It explains that the CLT states that the distribution of the sample mean will approach a normal distribution as the sample size increases, irrespective of the original population distribution. The script also reviews the characteristics of the sampling distribution of the sample mean, such as its mean being equal to the population mean and its standard deviation being equal to the population standard deviation divided by the square root of the sample size. The CLT's relevance is illustrated through a simulation using an exponential distribution, showing how the distribution of sample means becomes more normal as the sample size increases from 2 to 50. The video emphasizes the theorem's importance in statistical analysis, suggesting that a sample size of at least 30 is often a rough guideline for approximate normality.

05:05
๐Ÿ” Demonstrating CLT with Different Distributions

This paragraph continues the discussion on the Central Limit Theorem by conducting another simulation with a different, non-normal distribution. The simulation involves drawing samples of increasing sizes (from 2 to 50) and plotting the resulting sample means to observe their distribution. The script maintains the x-axis scaling across the plots while allowing the y-axis to adjust, demonstrating how the sample mean's distribution becomes increasingly normal with larger sample sizes. The importance of the CLT is highlighted again, noting that it allows for the use of normal distribution-based statistical inference procedures, even when the original population distribution is not normal, provided the sample size is sufficiently large.

10:06
๐Ÿง Applying CLT to Probability Calculations

The final paragraph of the script applies the Central Limit Theorem to a practical scenario involving salary distributions at a large corporation. It contrasts the probability calculation for a single employee's salary exceeding a certain amount with that of the average salary of a group of 100 employees. The script clarifies that while individual salaries are not normally distributed, the average salary of a sufficiently large group of employees can be approximated as normal due to the CLT. This allows for the use of z-scores and standard normal distribution to estimate probabilities. The video concludes by emphasizing the significance of the CLT in making statistical inferences and calculations possible, even in cases where the underlying population distribution is unknown or non-normal.

Mindmap
Keywords
๐Ÿ’กCentral Limit Theorem (CLT)
The Central Limit Theorem is a fundamental concept in statistics that states the distribution of sample means will approach a normal distribution as the sample size increases, regardless of the original distribution of the population. This theorem is central to the video's theme as it demonstrates how the distribution of sample means from non-normal populations can be approximated as normal for large enough sample sizes. The video illustrates this with simulations of different distributions, showing how increasing the sample size leads to a distribution that more closely resembles a normal curve.
๐Ÿ’กSample Mean
The sample mean, denoted as X bar in the script, is the average of a set of observations drawn from a population. It is a key concept in the video, as the Central Limit Theorem specifically discusses the distribution of sample means. The script explains that the mean of the sampling distribution of the sample mean is equal to the population mean, and as the sample size increases, the distribution of the sample mean tends toward normality, which is a direct application of the Central Limit Theorem.
๐Ÿ’กSampling Distribution
A sampling distribution is the probability distribution of a given statistic based on a random sample. In the context of the video, the sampling distribution of the sample mean is discussed in relation to the Central Limit Theorem. The script describes how the shape of this distribution changes as the sample size increases, eventually approximating a normal distribution, which is a direct consequence of the theorem.
๐Ÿ’กNormal Distribution
A normal distribution, also known as a Gaussian distribution, is a symmetric probability distribution that is defined by its mean and variance. The video emphasizes that the Central Limit Theorem allows the sample mean to be approximated as normally distributed for large sample sizes, even if the original population distribution is not normal. This is demonstrated through simulations where the histogram of sample means increasingly resembles a normal curve as the sample size grows.
๐Ÿ’กStandard Deviation
Standard deviation is a measure of the amount of variation or dispersion in a set of values. In the script, the standard deviation of the sampling distribution of the sample mean is described as being equal to the population's standard deviation (sigma) divided by the square root of the sample size (n). This concept is integral to understanding how the spread of the sample mean distribution changes with different sample sizes.
๐Ÿ’กPopulation Mean (mu)
The population mean, symbolized as mu in the script, is the average value of a population. It is a fundamental parameter in the discussion of the Central Limit Theorem, as the mean of the sampling distribution of the sample mean is equal to the population mean. The video uses the population mean as a reference point to illustrate how sample means are distributed around this central value.
๐Ÿ’กSample Size (n)
Sample size refers to the number of observations or individuals in a sample. The script demonstrates that as the sample size increases, the distribution of the sample mean approaches a normal distribution, which is a key aspect of the Central Limit Theorem. The video provides a rough guideline that a sample size of at least 30 can be considered large enough for the theorem to apply in most practical situations.
๐Ÿ’กExponential Distribution
An exponential distribution is a type of continuous probability distribution that is often used to model the time between events in a Poisson process. In the video, an exponential distribution is used as an example of a non-normal distribution from which samples are drawn. The simulation shows that even starting with such a distribution, the sample means' distribution will become more normal as the sample size increases, illustrating the Central Limit Theorem.
๐Ÿ’กHistogram
A histogram is a graphical representation of the distribution of a dataset, displaying the frequency or count of data points within specified intervals or 'bins'. In the video, histograms are used to visualize the sampling distribution of the sample mean for different sample sizes. The script describes how the shape of these histograms changes, becoming more bell-shaped (normal) as the sample size increases.
๐Ÿ’กSimulation
Simulation in the context of the video refers to the process of generating random samples from a given distribution and calculating the sample means. The script uses simulation to demonstrate the Central Limit Theorem by showing how the distribution of these sample means changes with increasing sample size. This method allows for a visual and practical understanding of the theorem's implications.
๐Ÿ’กZ-Score
A Z-score is a measure of how many standard deviations an element is from the mean. In statistics, it is used to standardize the distribution for comparison purposes. The video explains how the Central Limit Theorem allows for the use of Z-scores in calculating probabilities for sample means, even when the original population distribution is not normal, provided the sample size is large enough.
Highlights

The central limit theorem is a fundamental concept in statistics, stating that the sample mean will be approximately normally distributed for large sample sizes, regardless of the population distribution.

The mean of the sampling distribution of the sample mean is equal to the population mean.

The standard deviation of the sampling distribution of the sample mean is sigma over the square root of n.

If the population is normally distributed, the sample mean is also normally distributed.

The central limit theorem applies even if the population is not normally distributed, with the sample mean tending toward a normal distribution as sample size increases.

A simulation is used to illustrate the central limit theorem using an exponential distribution, which is not normal.

The shape of the distribution is more important than the scaling when observing the central limit theorem in action.

With a sample size of 2, the sampling distribution of the sample mean is not normal, even with a million simulations.

As sample size increases, the sampling distribution of the sample mean approaches a normal distribution.

A sample size of 50 is shown to produce a sampling distribution of the sample mean that is close to normal.

A rough guideline suggests that a sample mean can be considered approximately normally distributed if the sample size is at least 30.

The central limit theorem allows for the use of normal distribution-based statistical inference procedures even when sampling from non-normal populations, provided the sample size is large.

The theorem states that the sample mean tends in distribution to the standard normal distribution as the sample size tends to infinity.

Technical restrictions include the requirement for the mean and variance to be finite.

The central limit theorem facilitates probability calculations for sample means, even when the population distribution is unknown.

An example demonstrates how the central limit theorem can be used to calculate the probability of an average salary exceeding a certain value.

The importance of the central limit theorem in statistics is underscored by its ability to enable approximate probability calculations for large sample sizes.

The world of statistics would be very different without the central limit theorem, highlighting its foundational role.

Transcripts

Browse More Related Video

The Central Limit Theorem, Clearly Explained!!!

The Sampling Distribution of the Sample Mean

Elementary Stats Lesson #13

Central Limit Theorem & Sampling Distribution Concepts | Statistics Tutorial | MarinStatsLectures

6.4.1 The Central Limit Theorem - What the Central Limit Theorem Says and What It Doesn't Say

02 - What is the Central Limit Theorem in Statistics? - Part 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Central Limit TheoremStatisticsSamplingNormal DistributionSimulationData AnalysisPopulation MeanSample SizeStandard DeviationProbability Calculation