02 - What is the Central Limit Theorem in Statistics? - Part 1

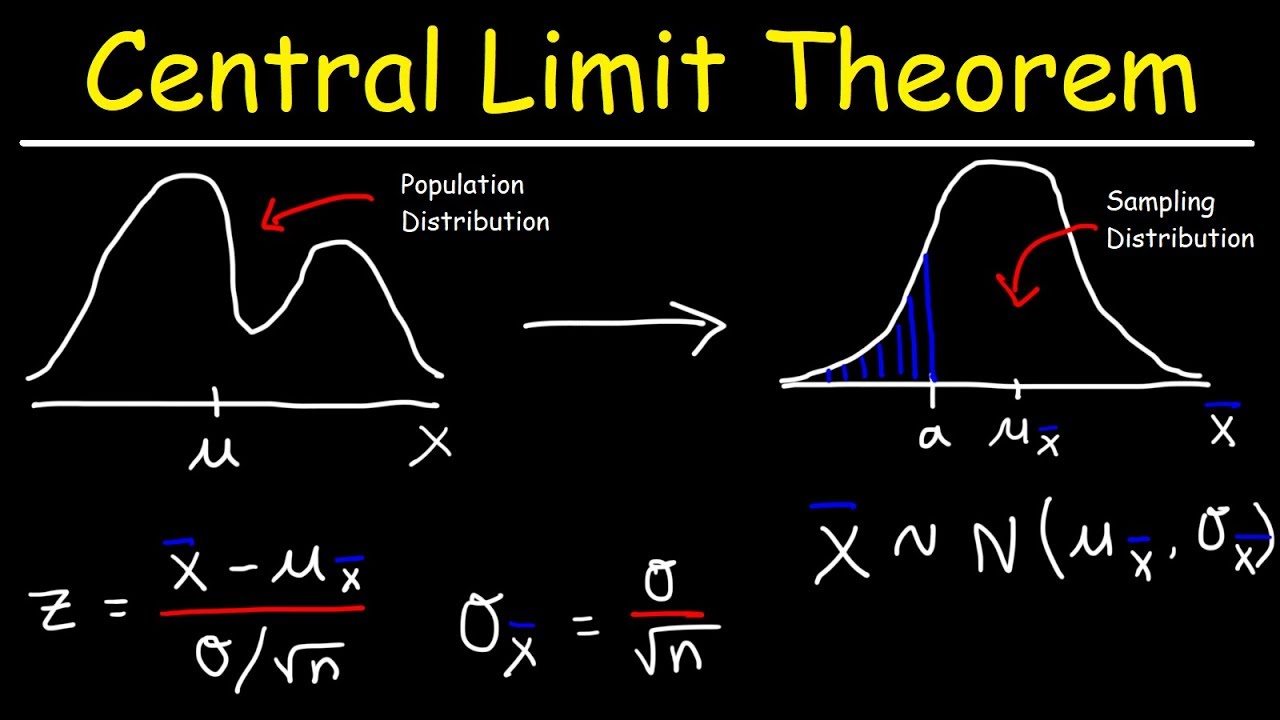
The first paragraph introduces the central limit theorem (CLT), emphasizing that while it can be challenging for students, the difficulty arises from the need to visualize the process rather than the complexity of the concept itself. The speaker sets expectations that understanding the CLT requires getting through the explanation and working through a few problems. The CLT is described as highly useful, especially when applied to problem-solving. The given population's mean (μ) and standard deviation (σ) are foundational to the discussion, and the concept of sampling from this population is introduced.

The second paragraph delves into the versatility of the CLT, highlighting its application regardless of the population's distribution shape. The process of sampling from a population of any distribution, calculating sample means, and the resulting distribution of these means is explained. The paragraph also touches on the theoretical aspect of sampling where every possible sample of a given size (n) is taken from the population. The practicality of the CLT is emphasized, noting its utility even when not every individual in the population is sampled.

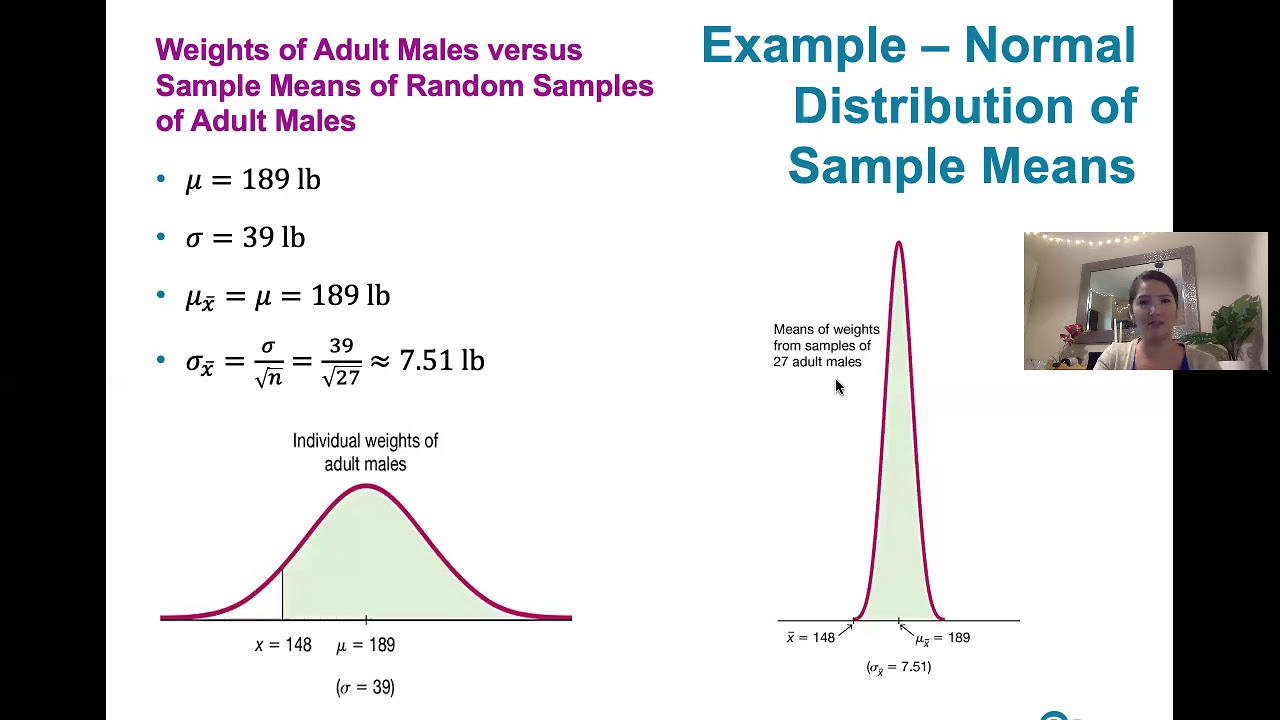
The third paragraph presents the core conclusions of the CLT. It states that the mean of all sample means will equal the population mean, irrespective of the sample size or the population's distribution. This is a powerful concept as it implies that by averaging enough sample means, one can approximate the population mean. The standard deviation of the sample means is also discussed, showing how it relates to the population standard deviation by a factor of the sample size's square root.

The fourth paragraph focuses on how to estimate the population's standard deviation using sample means and their standard deviation. It explains that by collecting multiple sample means and calculating their standard deviation, one can infer the population's standard deviation. The caveat of needing to sample the entire population to achieve this is acknowledged, but the paragraph clarifies that even without exhaustive sampling, a close approximation can be obtained through a large number of samples.

The fifth paragraph discusses the implications of the CLT when the population is normally distributed. It explains that if the population is normal, the distribution of sample means will also be normal, regardless of the sample size. The importance of this is underscored by the familiarity and ease with which statisticians can work with normal distributions. The concept is further extended to the scenario where the population is not normal but still results in a normal distribution of sample means if the sample size is greater than 30.

The sixth paragraph addresses the scenario where the population distribution is not normal. It clarifies that even with non-normal populations, if the sample size is greater than 30, the sampling distribution of sample means will approximate a normal distribution. This is a significant revelation as it implies that the shape of the original population distribution is not a limiting factor when applying the CLT with sufficiently large samples. The practical upshot is that one can still use normal distribution tables and methods to solve problems, which is particularly useful for statisticians.

The seventh and final paragraph provides a hypothetical example using the IQ distribution of MIT students to illustrate the CLT. It visualizes how even if the IQ distribution of MIT students is skewed due to selection bias, taking numerous samples of 30 students each and calculating their means will result in a normal distribution centered around the average IQ of MIT students. This example solidifies the concept that the CLT allows for the application of normal distribution methods to a wide array of distributions when the sample size is sufficiently large.