Entropy - 2nd Law of Thermodynamics - Enthalpy & Microstates

The Organic Chemistry Tutor

30 Mar 202129:45

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script delves into the concept of entropy, explaining spontaneous and non-spontaneous processes. It illustrates how processes like a ball rolling downhill are spontaneous, contrasting with cleaning a room, which is not. The script explores the relationship between entropy, probability, and the second law of thermodynamics, emphasizing that spontaneous processes tend to increase the universe's entropy. It uses examples like gas distribution and coin tosses to clarify how disordered states are more probable, leading to higher entropy. The script also discusses how to determine if a process is spontaneous based on heat flow and its impact on system and surroundings' entropy.

Takeaways

🔄 A spontaneous process is one that occurs naturally without external intervention, while a non-spontaneous process requires energy input to occur.
⛰️ The rolling of a ball down a hill is a spontaneous process, whereas rolling it up would be non-spontaneous.
🌿 Rusting of iron is a spontaneous process when exposed to air and water, happening naturally over time.
🧹 Cleaning a room is non-spontaneous as it requires work and does not happen by itself; rooms tend to become disorganized without intervention.
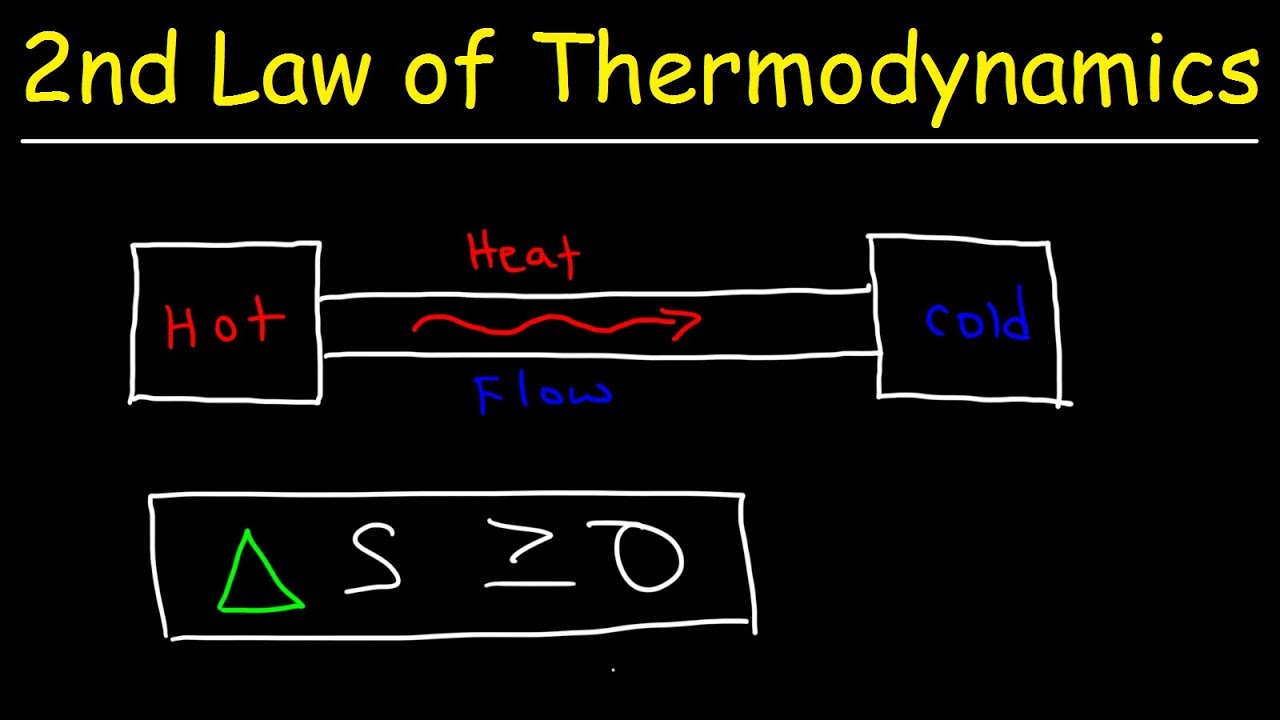
🔥 Heat naturally flows from hot to cold, which is a spontaneous process, but requires energy to reverse this flow, as seen in refrigerators.
💧 Gasoline reacts with air to produce carbon dioxide and water, a spontaneous process that can be accelerated with a spark.
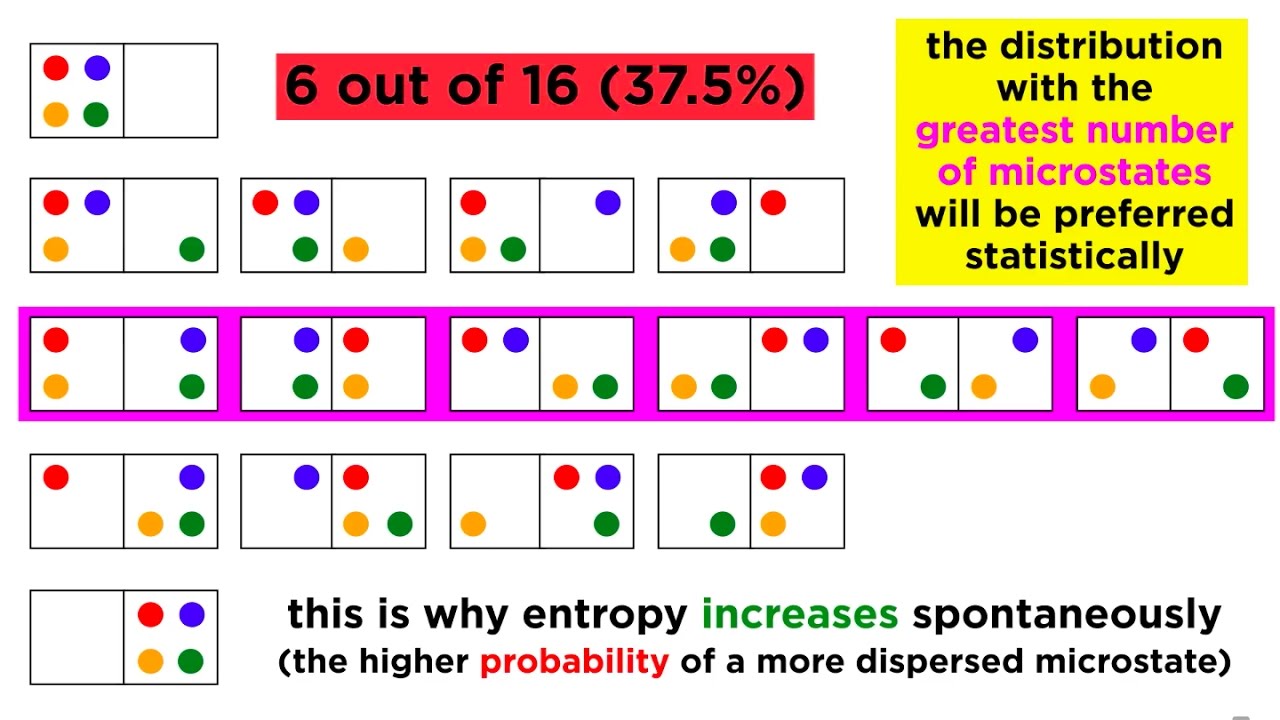
📈 The concept of positional probability relates to the number of microstates a system can occupy, with higher numbers indicating a more probable state.
🔄 Entropy is associated with the number of microstates; a system tends to move towards a state of higher entropy or greater disorder.
🎲 Flipping coins illustrates the principle of entropy, where a disorganized mix of heads and tails is more probable than all heads or all tails.
⚖️ The second law of thermodynamics states that the entropy of the universe increases for spontaneous processes and decreases for non-spontaneous ones.
🌡️ In an exothermic process, heat flows from the system to the surroundings, increasing the entropy of the surroundings and decreasing the system's entropy.

Q & A

What is a spontaneous process?
-A spontaneous process is one that can occur without any outside intervention. It happens naturally on its own.
Why is rolling a ball down a hill considered a spontaneous process?
-Rolling a ball down a hill is a spontaneous process because it will naturally occur on its own without any external force or energy input.
What does it mean for a process to be non-spontaneous?
-A non-spontaneous process is one that does not happen on its own and requires energy or work to be initiated or to continue.
How does the rusting of iron in the presence of air and water illustrate a spontaneous process?
-The rusting of iron is a spontaneous process because it will naturally occur over time when iron is exposed to air and water, without any additional intervention.
Why is cleaning a bedroom considered a non-spontaneous process?
-Cleaning a bedroom is non-spontaneous because it requires work and energy to organize and tidy up the space, which does not happen naturally on its own.
What is the relationship between entropy and the probability of a state?
-Entropy is associated with the probability of a state. Higher entropy indicates a higher number of microstates, making a state more probable or likely to occur.
Why do spontaneous processes tend to increase the disorder of a system?
-Spontaneous processes tend to increase disorder because disordered states generally have a higher number of microstates, making them more probable than ordered states.
How does the tossing of four coins illustrate the concept of entropy and probability?
-When tossing four coins, the most probable outcome is a mix of heads and tails, which represents a higher entropy state compared to the less probable outcomes of all heads or all tails.
What does the second law of thermodynamics state about the entropy of the universe in relation to spontaneous processes?
-The second law of thermodynamics states that for a spontaneous process, the change in the entropy of the universe is positive, indicating an increase in overall disorder.
How does the concept of microstates relate to the entropy of a system?
-The number of microstates in a system is directly related to its entropy. A system with more microstates has higher entropy, reflecting a greater degree of disorder or randomness.
Why is it improbable for all molecules in a container to be on one side, according to the script?
-It is improbable for all molecules to be on one side of a container because this state has fewer microstates, indicating a lower probability compared to a distribution that maximizes microstates, such as an even spread of molecules.

Outlines

00:00

🔄 Understanding Spontaneity and Entropy

This paragraph introduces the concept of spontaneous and non-spontaneous processes in relation to entropy. It explains that a spontaneous process occurs naturally without external influence, while a non-spontaneous process requires energy input. The paragraph uses the analogy of a ball rolling down a hill to illustrate a spontaneous process and the difficulty of rolling it back up as non-spontaneous. It also discusses the spontaneous rusting of iron and the non-spontaneous act of cleaning a room, emphasizing that natural processes tend toward increased disorder. The paragraph concludes by identifying the cleaning of a room as a non-spontaneous process due to the work required to achieve order.

05:01

📈 Calculating Microstates and Positional Entropy

The second paragraph delves into calculating the number of microstates to determine the positional probability and entropy of different systems. It explains that gases naturally expand to fill containers, representing a state of high positional probability. The paragraph provides examples of calculating microstates for different systems, such as one with all molecules on one side of a container, another with a single molecule on one side, and a system with an equal distribution of molecules. It concludes that system B, with an equal distribution of molecules, has the highest number of microstates and thus the highest positional entropy, making it the most probable state.

10:02

🎲 The Probability Driving Spontaneous Processes

This paragraph explores the idea that the driving force behind spontaneous processes is an increase in probability, with disordered states being more probable than ordered ones. It uses the example of organizing and disorganizing a room to illustrate this point and explains that natural processes tend toward higher entropy or more disorder. The paragraph also discusses the tossing of coins to demonstrate how the probability of a disorganized outcome (a mix of heads and tails) is higher than that of an organized outcome (all heads or all tails). It concludes by emphasizing that the entropy of a system increases as the number of microstates increases, aligning with the tendency of natural processes to move toward higher probability and disorder.

15:04

🔢 Entropy and Coin Tossing Probabilities

The fourth paragraph examines the relationship between entropy and the probability of disorganized states using the example of coin tossing. It explains how the probability of achieving an organized state (all heads or all tails) decreases as the number of coins increases, while the probability of a disorganized state (a mix of heads and tails) increases. The paragraph calculates the probabilities for different numbers of coins and illustrates that with a large number of coins, such as Avogadro's number, the chance of all coins landing on one side becomes negligible. It concludes by reinforcing the idea that the probability of a disorganized state increases with the number of particles involved, aligning with the second law of thermodynamics.

20:05

⚙️ Entropy and the Second Law of Thermodynamics

This paragraph discusses the second law of thermodynamics in the context of entropy changes in spontaneous, reversible, and non-spontaneous processes. It explains that for a spontaneous process, the entropy change of the universe is positive, indicating an increase in disorder. For a process at equilibrium, the entropy change is zero, and for a non-spontaneous process, the entropy change is negative, indicating a decrease in disorder. The paragraph also addresses common misconceptions about the entropy changes of the system and surroundings, emphasizing that these changes can be positive or negative and are not always in the same direction. It concludes by identifying statement D as the true statement that the entropy change of the universe is negative for a non-spontaneous process.

25:05

🌡️ Entropy Changes in Exothermic Processes

The final paragraph examines the entropy changes in an exothermic spontaneous process, focusing on the direction of heat flow and its impact on the entropy of the system and surroundings. It explains that during an exothermic process, heat flows from the hot system to the colder surroundings, leading to an increase in entropy for the surroundings and a decrease in entropy for the system. The paragraph also discusses the relationship between temperature and entropy, noting that higher temperatures correspond to higher entropy values. It concludes by evaluating statements about the entropy changes in the system, surroundings, and universe, identifying statements B, C, and D as true, indicating that the entropy of the surroundings increases, the entropy of the universe increases for a spontaneous process, and the entropy of the system decreases.

Mindmap

Keywords

💡Spontaneous process

A spontaneous process is one that occurs naturally without any external influence or intervention. In the context of the video, it is used to describe processes such as a ball rolling down a hill or iron rusting when exposed to air and water. These processes are highlighted as examples to illustrate what constitutes a spontaneous change according to the second law of thermodynamics.

💡Non-spontaneous process

A non-spontaneous process is one that does not occur naturally and requires external energy or work to proceed. The video uses the example of a ball rolling uphill, which cannot happen on its own without the input of energy, to explain this concept. It is the opposite of a spontaneous process and is integral to understanding entropy and the direction of natural processes.

💡Entropy

Entropy is a thermodynamic property that measures the degree of disorder or randomness in a system. The video script discusses entropy in relation to spontaneous and non-spontaneous processes, emphasizing that natural processes tend to increase entropy, moving towards a state of greater disorder. It is a central theme in the discussion of why certain processes occur spontaneously while others do not.

💡Microstates

Microstates refer to the different possible arrangements of particles in a system. The video explains that a system with a higher number of microstates is more probable and thus more likely to be the natural state of a system. It uses the analogy of gas particles spreading out to fill a container to illustrate that the most probable state has the highest positional probability and entropy.

💡Probability

In the video, probability is discussed as the driving force behind spontaneous processes. It is the likelihood of a particular state or arrangement occurring. The script explains that disordered states are more probable than ordered states, which is why natural processes tend to increase in entropy. The concept is exemplified by the tossing of coins, where a mix of heads and tails is more probable than all heads or all tails.

💡Second law of thermodynamics

The second law of thermodynamics is a fundamental principle stating that the total entropy of an isolated system can never decrease over time. The video script uses this law to explain the direction of spontaneous processes, stating that for a process to be spontaneous, the change in the entropy of the universe must be positive.

💡Exothermic process

An exothermic process is one that releases energy, usually in the form of heat, to its surroundings. In the video, it is mentioned in the context of a spontaneous process where the system's temperature is higher than the surroundings, leading to a flow of heat from the system to the surroundings, resulting in an increase in entropy of the surroundings.

💡Endothermic process

Although not explicitly defined in the script, an endothermic process is the opposite of an exothermic one, where a system absorbs energy from its surroundings. The script implies this concept when discussing the transfer of heat in relation to entropy changes, suggesting that an endothermic process would decrease the entropy of the surroundings.

💡Equilibrium

Equilibrium in the context of the video refers to a state where the forward and reverse reactions occur at the same rate, resulting in no net change in the system. It is mentioned in relation to reversible reactions and is associated with a change in the entropy of the universe being zero.

💡Disorder

Disorder, as discussed in the video, is a state of increased randomness or lack of organization in a system. It is closely related to the concept of entropy, with higher entropy indicating greater disorder. The script uses the example of a room becoming disorganized over time to illustrate how natural processes tend towards states of higher disorder.

💡Organization

Organization is the opposite of disorder and refers to a state of arrangement or order. The video contrasts organization with disorder when discussing entropy, noting that while there are many ways to disorder a room, there are fewer ways to keep it organized. This illustrates why natural processes tend to move towards increased entropy and disorder rather than organization.

Highlights

A spontaneous process is one that occurs naturally without outside intervention.

Non-spontaneous processes require energy input to occur.

A ball rolling down a hill exemplifies a spontaneous process.

Cleaning a room is a non-spontaneous process as it requires work.

Heat naturally flows from hot to cold, illustrating a spontaneous process.

Gasoline's reaction with air to produce carbon dioxide is spontaneous but slow.

The driving force for a spontaneous process is an increase in probability.

Disordered states are more probable than ordered states, leading to higher entropy.

The concept of microstates is introduced to explain the most probable state of a system.

Calculating the number of microstates can determine the system's positional entropy.

The most probable state of a system has the highest number of microstates.

Flipping coins illustrates the concept of increasing disorder and decreasing probability of an organized outcome.

The second law of thermodynamics relates to the entropy of the universe in spontaneous and non-spontaneous processes.

The entropy of the universe is the sum of the system's and surroundings' entropy changes.

Spontaneity of a process is determined by comparing the magnitudes of entropy changes in the system and surroundings.

An exothermic process results in a decrease in the system's entropy and an increase in the surroundings' entropy.

The entropy of the universe always increases for a spontaneous process according to the second law of thermodynamics.

Transcripts

Browse More Related Video

Second Law of Thermodynamics - Heat Energy, Entropy & Spontaneous Processes

What is entropy? - Jeff Phillips

The Second Law of Thermodynamics: Heat Flow, Entropy, and Microstates

6.2 Entropy, Gibbs Free Energy, and the Equilibrium Constant | Organic Chemistry

Understanding Second Law of Thermodynamics !

Entropy: Embrace the Chaos! Crash Course Chemistry #20

Related Tags

Entropy Spontaneity Thermodynamics Natural Processes Energy Conversion Order and Chaos Heat Transfer Probability Theory Second Law Disorder