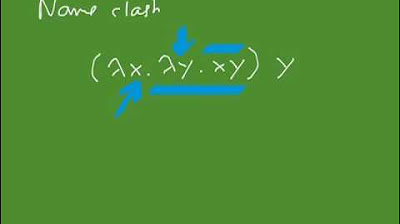Weak head normal form WHNF
TLDRThe script delves into the concept of Weak Head Normal Form (WHNF) in lambda calculus, a fundamental aspect of functional programming languages like Haskell or Miranda. It explains that a term in WHNF either starts with a variable followed by any term or a lambda abstraction with a WHNF body. The script contrasts WHNF with normal forms, illustrating that while all normal forms are WHNFs, not all WHNFs are normal forms. It uses examples to demonstrate the properties and differences, highlighting the importance of WHNF in evaluating and reducing lambda expressions.
Takeaways
- 😀 A weak head normal form (abbreviated as WHNF) in lambda calculus is a term that satisfies specific properties, different from normal form.
- 📌 The first property of WHNF is that a lambda term must be in the form of \( \lambda x . p \) where \( p \) is any lambda term.
- 🔍 The second property is that a term can be in the form of \( \lambda x \, P_1 \, ... \, P_n \) where \( n \geq 0 \) and \( P_1, ..., P_n \) are arbitrary lambda terms, with \( x \) being a variable.
- 🌐 Every normal form is a weak head normal form, but not every WHNF is a normal form, indicating a hierarchy in the reduction process.
- 🔑 The identity lambda term \( \lambda x \, x \) is both a WHNF and a normal form, satisfying both sets of properties.
- 🚫 A term like \( \lambda x \) does not have a normal form because it can be reduced indefinitely, but it is a WHNF due to its structure.
- 🔄 The term \( \lambda x \, (M \, x) \) is a WHNF but not a normal form because it can be reduced further, illustrating the difference between the two concepts.
- 📚 The script explains that a term in WHNF will always remain in the form \( \lambda x \, P' \) after reduction, emphasizing the stability of the head position.
- ♻️ The concept of better reduction is introduced, which is a relation that is reflexive, symmetric, and transitive, underpinning the reduction process.
- 🔑 The script uses the transitive, symmetric, reflexive closure of better reduction to explain the persistence of the head variable \( x \) in WHNF after reduction.
- 📉 The difference between WHNF and normal form is highlighted through examples, showing that WHNF is a broader category that includes terms that can still be reduced.
- 🔬 The script concludes by emphasizing the intuition behind WHNF, where the head of the term remains unchanged no matter the reduction process.
Q & A
What is a weak head normal form (WHNF) in lambda calculus?
-A weak head normal form (WHNF) is a lambda term that satisfies certain properties. It can be in one of two forms: 1) \( \lambda x . p \) where \( p \) is any lambda term, or 2) \( x \) \( P_1 \) ... \( P_n \) where \( n \geq 0 \) and \( P_1 \) to \( P_n \) are any lambda terms with \( x \) being a variable.
What is the difference between weak head normal form and normal form?
-Every normal form is a weak head normal form, but not every weak head normal form is a normal form. A normal form is a lambda term that cannot undergo any more reductions, whereas a weak head normal form can still have reducible parts but maintains a specific structure in its head.
What are the two patterns that define a weak head normal form?
-The two patterns are: 1) \( \lambda x . p \) where \( p \) is any lambda term, and 2) \( x \) \( P_1 \) ... \( P_n \) where \( n \geq 0 \), \( x \) is a variable, and \( P_1 \) to \( P_n \) are any lambda terms.
Can a lambda term be in both weak head normal form and normal form?
-Yes, a lambda term can be in both weak head normal form and normal form. For example, the identity lambda term \( \lambda x . x \) is both a weak head normal form and a normal form.
Why is the term \( \lambda x . \text{identity of } x \) considered a weak head normal form but not a normal form?
-The term \( \lambda x . \text{identity of } x \) is considered a weak head normal form because it satisfies the property of having a variable in the head position. However, it is not a normal form because the body of the lambda can be reduced further.
What is an example of a lambda term that is in weak head normal form but not in normal form?
-An example is \( \lambda x . x \) applied to an identity combinator. It is in weak head normal form because it maintains the head structure, but it is not in normal form because the body can be reduced.
What is the significance of the variable \( x \) in the definition of a weak head normal form?
-In the definition of a weak head normal form, the variable \( x \) must be in the first position. This ensures that the term maintains a specific structure in its head, which is crucial for the properties of weak head normal forms.
How does the concept of better reduction relate to weak head normal forms?
-Better reduction is used to determine the transitive, symmetric, and reflexive closure of reductions. It helps in understanding how a term in weak head normal form will always remain in a specific form no matter how it is reduced.
What is the relationship between the properties of reflexivity, symmetry, and transitivity in the context of lambda calculus?
-Reflexivity, symmetry, and transitivity are properties used to define the better reduction relation in lambda calculus. Reflexivity ensures that a term is always reducible to itself, symmetry allows for reductions in both directions, and transitivity ensures that if a term can be reduced to another and that term can be further reduced, the original term can be reduced to the final term.
Why is it important to distinguish between weak head normal form and normal form in lambda calculus?
-Distinguishing between weak head normal form and normal form is important because it helps in understanding the structure and behavior of lambda terms. It provides insights into how terms can be reduced and what their final forms might look like after reduction.
Outlines
📚 Introduction to Weak Head Normal Form in Lambda Calculus
This paragraph introduces the concept of weak head normal form (WHNF) in the context of lambda calculus, particularly in languages like Haskell or Miranda. It explains that a lambda term in WHNF has a specific structure, either starting with a lambda abstraction followed by a variable and a term, or a variable applied to a series of terms. The paragraph also distinguishes between WHNF and normal form, noting that while every normal form is a WHNF, not every WHNF is a normal form. Examples are provided to illustrate these concepts, such as the identity lambda term, which is both a WHNF and a normal form, and the variable X, which is a WHNF but not a normal form due to its reducible body.
🔍 Further Exploration of Weak Head Normal Form
The second paragraph delves deeper into the properties and implications of weak head normal form. It discusses the conditions under which a lambda term is considered to be in WHNF, emphasizing the importance of the first part of the term being reducible. The paragraph also explores the relationship between WHNF and normal form, highlighting that terms in WHNF can undergo reduction but may not necessarily reach a normal form. Examples are given to illustrate terms that are in WHNF but not in normal form, such as the combinator 'X', which can be reduced indefinitely. The paragraph concludes by explaining the intuition behind WHNF, suggesting that it represents a form that can be reduced but will always retain its initial structure, with the variable 'X' remaining in the first position.
Mindmap
Keywords
💡Weak Head Normal Form (WHNF)
💡Lambda Term
💡Normal Form
💡Reduction
💡Identity Lambda Term
💡Combinator
💡Variable
💡Reflexivity, Symmetry, and Transitivity
💡Better Reduction
💡Reduction Inside
💡Infinite Reduction Steps
Highlights
Weak head normal form (WHNF) is a specific property of Lambda terms in some functional programming languages like Haskell or Miranda.
A Lambda term in WHNF has one of two forms: either '(\ x . p)' where 'p' is any term, or 'x P1 ... PN' with 'x' a variable and 'P1 ... PN' any Lambda terms.
Every normal form is a weak head normal form, but not every WHNF is a normal form.
The identity Lambda term is both a WHNF and a normal form due to satisfying the properties of both.
A term in WHNF remains in the form 'Lambda x. P' after reduction, where 'P' is a reducible term.
A normal form cannot be reduced further, unlike a WHNF which may still undergo reduction.
The variable 'X' in 'Lambda X' is an example of a term that is in WHNF but not in normal form because it can be reduced.
A term like 'Lambda X X' is both in WHNF and normal form because it satisfies the second pattern with 'N' equal to zero.
The term 'Lambda X (identity of X)' is a WHNF because it meets the criteria but is not a normal form due to reducibility of its body.
The combinator 'X' is a WHNF but lacks a normal form because it can be reduced infinitely.
A term in WHNF will always remain in the form 'Lambda x. P' or 'X P1 ... PN' after reduction, maintaining the position of 'X'.
The 'P1 Prime to PN Prime' in the term 'X P1 ... PN' are the results of better reduction applied to the initial 'Pi' terms.
The concept of better reduction is integral to understanding the transitive, symmetric, and reflexive properties of WHNF.
The 'E' situation in the transcript refers to the first pattern of WHNF, emphasizing the importance of the variable 'X'.
The second situation in the transcript discusses the transitive and symmetric properties of WHNF, focusing on the variable 'X' and the terms 'P1 ... PN'.
The intuition behind WHNF is that the first part of a term can be reduced without affecting the overall form, as demonstrated by the 'Lambda x. P' structure.
The transcript explains that WHNF is a state where a term, once reduced, will always maintain a specific form, highlighting its importance in functional programming.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: