Example (2.2) - Finding the limit of a function #11 (Calc)

Cory Sheeley
16 Oct 201803:15
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the presenter tackles the challenge of finding the limit of a function as T approaches 11. Initially, it's clear that direct substitution results in division by zero, prompting the need for factoring. The presenter skillfully demonstrates how to factor the quadratic expressions in the numerator and denominator, leading to the cancellation of the (T-11) term. This strategic approach removes the domain error and allows for a successful evaluation of the limit, which is found to be 25 over 22. The video serves as an excellent tutorial for those looking to sharpen their factoring skills and understand how to handle limits that initially seem undefined.

Takeaways
  • 📚 The video is about finding the limit of a function as T approaches 11.
  • ❗ The function cannot be directly evaluated at T=11 due to division by zero.
  • 🔍 Factoring is suggested as a method to simplify the function and avoid undefined behavior.
  • 🔑 The function given is \( T^2 + 3T - 150 \) over \( T^2 - 121 \).
  • 🧩 The top part of the function factors into \( (T + 14)(T - 11) \).
  • 🧩 The bottom part of the function factors into \( (T - 11)(T + 11) \).
  • 🤔 The challenge is to find two numbers that multiply to -154 and add up to 3T.
  • 🔢 The numbers found are 14 and -11, which satisfy the conditions for the top part of the function.
  • 💡 The term \( T - 11 \) in the numerator and denominator will cancel each other out.
  • 🔄 After canceling, the simplified expression becomes \( (T + 14) / (T + 11) \).
  • 🎯 The limit as T approaches 11 is calculated by substituting T with 11, resulting in \( 25/22 \).
Q & A

  • What is the function given in the script for which the limit is being evaluated?

    -The function given is (T^2 + 3T - 150) / (T^2 - 121).

  • Why can't we directly plug in T=11 into the function to find the limit?

    -We can't plug in T=11 directly because it results in division by zero, which is undefined.

  • What mathematical concept is being tested in this script?

    -The mathematical concept being tested is factoring, specifically the factoring of quadratic expressions.

  • What are the two numbers that are factors of -154 that add up to 3T?

    -The two numbers are 14 and -11, which add up to 3T and multiply to give -154.

  • What is the purpose of factoring the quadratic expressions in the numerator and denominator?

    -The purpose is to simplify the expression and potentially cancel out terms, which can help in evaluating the limit without encountering a domain error.

  • What is the factored form of the numerator after identifying the correct factors?

    -The factored form of the numerator is (T + 14)(T - 11).

  • What is the factored form of the denominator after identifying the correct factors?

    -The factored form of the denominator is (T + 11)(T - 11).

  • What happens when T=11 is substituted into the simplified expression?

    -The term (T - 11) cancels out, leaving us with (T + 14) / (T + 11), which simplifies to 25/22 when T=11.

  • What is the limit of the function as T approaches 11 according to the script?

    -The limit of the function as T approaches 11 is 25/22.

  • Why is the process of factoring important in evaluating limits?

    -Factoring is important because it can simplify expressions and reveal opportunities to cancel terms, which can help in evaluating limits without encountering undefined operations like division by zero.

  • What is the final step in evaluating the limit after factoring and canceling terms?

    -The final step is to substitute the value T=11 into the simplified expression and calculate the result, which gives the limit.

Outlines
00:00
📚 Factoring to Find the Limit

In this educational video segment, the presenter introduces a limit problem from section 2.2, focusing on finding the limit as T approaches 11 for a given function. Initially, it's noted that plugging in T=11 results in a division by zero, which is undefined. To circumvent this, the presenter suggests factoring the function to eliminate the division by zero. The function in question is T^2 + 3T - 150 over T^2 - 121. The presenter guides through the factoring process, identifying factors of -154 that add up to 3T and factors of 121 that will allow for cancellation. The top polynomial is factored into (T + 14)(T - 11), and the bottom into (T + 11)(T - 11). After factoring, the (T - 11) terms cancel out, simplifying the function to (T + 14) / (T + 11). Substituting T=11 into the simplified function yields the limit as 25/22.

Mindmap
Keywords
💡Limit
In mathematics, a 'limit' refers to the value that a function or sequence approaches as the input or index approaches some value. In the context of the video, the limit is being calculated for a specific function as the variable T approaches 11. The script demonstrates the process of finding this limit, which is a fundamental concept in calculus.
💡Function
A 'function' is a mathematical relationship between two sets that assigns to each element from the domain exactly one element from the codomain. The video script discusses a specific function, which is given by a rational expression, and the process of evaluating its limit as T approaches 11.
💡Factoring
Factoring is the process of breaking down a polynomial into a product of its factors, which are simpler polynomials. In the script, factoring is used as a method to simplify the given function and cancel out terms, making it possible to evaluate the limit without encountering division by zero.
💡Domain Error
A 'domain error' occurs when a function is evaluated at a point where it is not defined, such as division by zero. The script mentions the need to avoid a domain error by factoring the function to cancel out the term that would cause division by zero when T equals 11.
💡T
In the script, 'T' is the variable of the function for which the limit is being evaluated. It is a placeholder for the input value in the function, and the process involves finding the limit as T approaches a specific value, which is 11 in this case.
💡Quadratic
A 'quadratic' is a polynomial of degree 2. In the video, the numerator and denominator of the function are quadratic expressions, and the process of factoring these quadratics is crucial for simplifying the function and finding the limit.
💡Binomials
Binomials are algebraic expressions with two terms. The script refers to breaking down the quadratic expressions into sets of binomials, which is part of the factoring process to simplify the function.
💡Factor Pairs
Factor pairs are pairs of numbers that multiply together to give a certain product. In the script, the factor pairs for the constant terms in the quadratic expressions are identified to facilitate the factoring process.
💡Cancellation
Cancellation is the process of eliminating a term from both the numerator and the denominator of a fraction, which simplifies the expression. In the context of the video, cancellation is used to simplify the function after factoring, allowing for the limit to be evaluated without division by zero.
💡Rational Expression
A 'rational expression' is a fraction where both the numerator and the denominator are polynomials. The function in the script is a rational expression, and the process of finding its limit involves simplifying this expression to avoid undefined operations.
💡Undefined
In mathematics, a term or expression is 'undefined' when it does not have a value, such as division by zero. The script discusses avoiding an undefined expression by factoring and canceling terms in the function to ensure the limit can be evaluated.
Highlights

Finding the limit of a function as T approaches 11, with initial evaluation showing a division by zero issue.

Introduction of the need for factoring to avoid domain errors in limit evaluation.

Demonstration of factoring the numerator T^2 + 3T - 150 into (T + 14)(T - 11).

Explanation of finding factors of -154 that add up to 3T, which are 14 and -11.

Factoring the denominator T^2 - 121 into (T + 11)(T - 11), recognizing it as a difference of squares.

Cancellation of (T - 11) terms in the numerator and denominator to simplify the expression.

Illustration of how the domain error is resolved after factoring and cancellation.

Substitution of T with 11 in the simplified expression to find the limit.

Final calculation of the limit as T approaches 11, resulting in the value 25/22.

Emphasis on the importance of factoring skills in evaluating limits of functions.

Highlighting the method of avoiding undefined expressions in limit calculations.

Use of a specific example to demonstrate the process of factoring and limit evaluation.

Step-by-step walkthrough of the factoring process for both the numerator and the denominator.

Clarification of the concept of domain errors and how they are circumvented.

Application of the difference of squares formula in factoring the denominator.

Visual representation of the cancellation process in the function's expression.

Explanation of the final step in limit evaluation after simplification.

Conclusion of the limit evaluation process with the final result.

Transcripts

Browse More Related Video

Example (2.2) - Finding the limit of a function #10 (Calc)

Example (2.2) - Finding the limit of a function #15 (Calc)

Example (2.2) - Finding the limit of a function #14 (Calc)

Example (2.2) - Finding the limit of a function #12 (Calc)

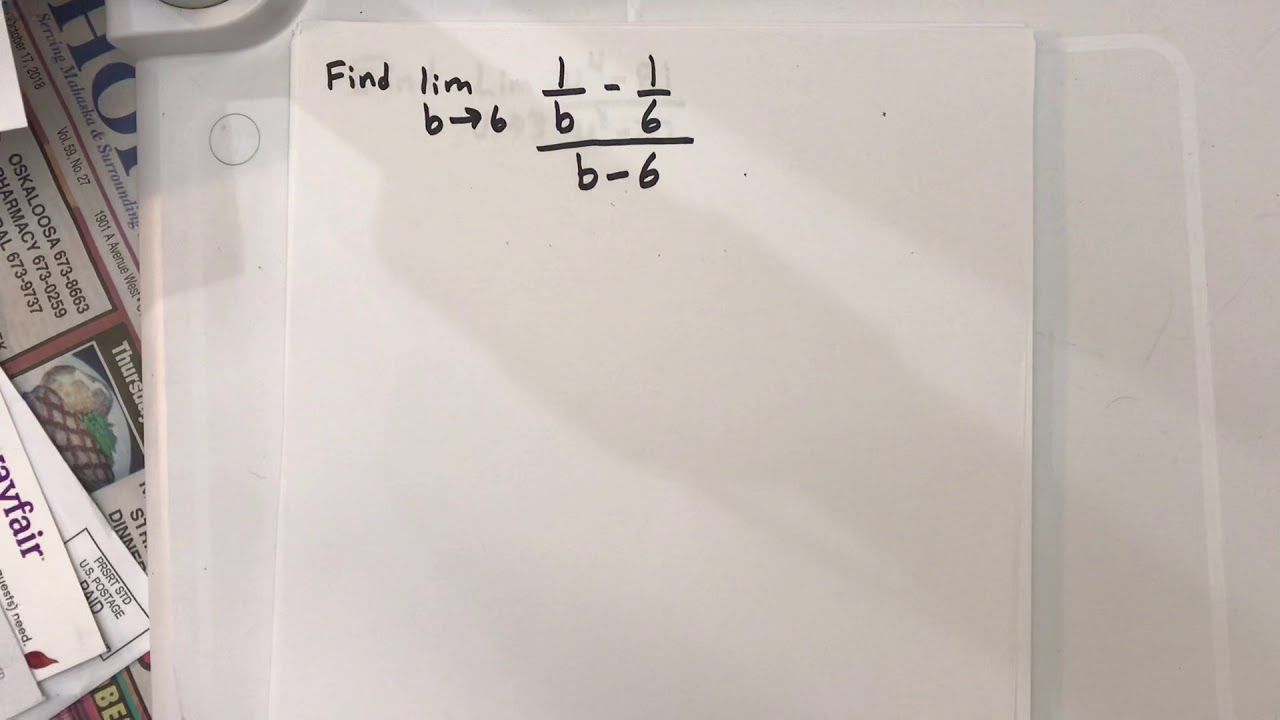
Example (2.2) - Finding the limit of a function #13 (Calc)

2.2 - Problem #4 (Calc)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusLimitFactoringSimplificationMathematicsEducationalTutorialFunction AnalysisCritical ThinkingProblem Solving