Lecture 16: Economics and Architecture
TLDRThis lecture explores optimization concepts through economics and architecture. It discusses maximizing business profit by balancing revenue and cost functions, using calculus to determine optimal production levels. An architectural example involves finding the best viewing distance for a museum artwork by maximizing the viewing angle. The lecture also delves into historical challenge problems, such as describing the curve of a hanging chain (catenary) and the brachistochrone problem, which seeks the fastest curve for an object to slide down under gravity. The video concludes with an introduction to the calculus of variations, exemplified by Dido's problem, concerning the shape that encloses the maximum area using a fixed length of material.
Takeaways
- 📈 Optimization in economics is about maximizing profit by finding the right balance between revenue and cost functions.
- 🔍 In business, the cost function includes fixed costs and variable costs, while revenue depends on the quantity of goods sold and their selling price.
- 📊 To maximize profit, one should produce the quantity of goods where the marginal revenue equals the marginal cost, which is found by setting their derivatives equal to each other.
- 📉 The graph of revenue typically shows a maximum point, indicating the peak of potential sales before demand drops off.
- 🏛 The concept of optimization extends beyond economics into architecture, such as finding the optimal viewing position for a piece of art in a museum.
- 🎨 The shape of a hanging chain, known as a catenary, is an example of a challenge problem from the 17th century that was solved using calculus.
- 🌉 The inverted catenary shape is ideal for arches due to the equilibrium of horizontal forces, as exemplified by the St. Louis Arch.
- 🚴♂️ An interesting property of the catenary is that a road made of inverted catenaries could allow for smooth bicycle riding with square wheels.
- 📉 The brachistochrone problem, posed by Johann Bernoulli, sought the curve of fastest descent for a point under the influence of gravity, which was found to be a cycloid.
- 🏰 Dido's problem from Virgil's Aeneid is an optimization problem that asks for the shape of a curve that encloses the maximum area with a given perimeter, which is proven to be a circle.
- 🔁 The cycloid curve has the unique property of being an isochrone, meaning a ball rolling down from any point on the curve reaches the bottom in the same amount of time.
Q & A
What is the basic concept of optimization in the context of business?
-The basic concept of optimization in business involves maximizing profit. This is achieved by finding the right balance between revenue and cost, where the profit, which is the difference between revenue and cost, is at its maximum.
How does a company determine the optimal number of goods to produce for maximum profit?
-A company determines the optimal number of goods to produce by using calculus to analyze the cost function and the revenue function. The goal is to find the point where the marginal revenue (the derivative of the revenue function) equals the marginal cost (the derivative of the cost function), which indicates the production level that maximizes profit.
What are marginal cost and marginal revenue in economic terms?
-In economic terms, marginal cost refers to the derivative of the cost function, which is the additional cost incurred in producing one more unit of a good. Marginal revenue is the derivative of the revenue function, representing the additional revenue generated from selling one more unit of a good.
Can you provide an example of how a company might use calculus to maximize profit?
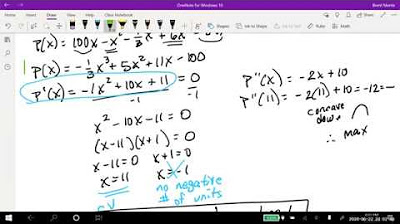
-An example provided in the script involves a company with a fixed cost of $100,000 and a variable cost of $30 per unit. The cost function is 100,000 + 30x, with a derivative of 30. The revenue function depends on the price and quantity sold, and the example given is 400x - x^2/50. The marginal revenue is 400 - x/25. The maximum profit occurs when the marginal revenue equals the marginal cost, which upon solving gives x = 9,250 units as the optimal production level for maximum profit.
What is the significance of the catenary curve in architecture?
-The catenary curve, the shape of a hanging chain, is significant in architecture because it represents a natural equilibrium of forces. An inverted catenary is an excellent shape for an arch, as the forces are tangential along the arch, as exemplified by the St. Louis Arch.
Why is the catenary curve also known as an isochrone curve?
-The catenary curve is known as an isochrone curve because it has the property that a ball rolling down from any point on the curve will reach the bottom in the same amount of time, making it an ideal shape for certain structures where consistent timing is desired.
What was the brachistochrone problem and who solved it?
-The brachistochrone problem, posed by Johann Bernoulli in 1696, was a challenge to find the curve of fastest descent for a point particle sliding down under the influence of gravity. The problem was solved by Johann Bernoulli, Jacob Bernoulli, the Marquis de l'Hôpital, and independently by both Leibniz and Newton.
What shape allows an object to slide down under gravity in the quickest possible time?
-The shape that allows an object to slide down under gravity in the quickest possible time is the cycloid, a curve traced by a point on the circumference of a rolling circle.
What is Dido's problem and what is the optimal solution?
-Dido's problem, named after Queen Dido from Virgil's Aeneid, is an optimization problem where the goal is to enclose the maximum area with a fixed length of material, such as the hide of an ox. The optimal solution is to form a circle, as it encloses the maximum area for a given perimeter.
What is the calculus of variations and how does it relate to the problems discussed in the script?
-The calculus of variations is a field of mathematics that deals with optimization problems, often involving finding the shape of a curve that maximizes or minimizes a certain quantity. It relates to the problems discussed in the script, such as the catenary, brachistochrone, and Dido's problem, where the goal is to find the optimal curve for a given set of conditions.
Outlines
📈 Optimization in Economics and Architecture
This paragraph introduces the concept of optimization, using calculus to maximize profits in economics and to find optimal viewing angles in architecture. The speaker explains how a company's profit is the difference between revenue and cost, and how calculus can be used to determine the optimal quantity of goods to produce for maximum profit. The paragraph also touches on the idea of marginal cost and revenue, which are the derivatives of their respective functions. An example is provided with a cost function and a revenue function, demonstrating how to set their derivatives equal to find the quantity that maximizes profit.
📊 Derivatives and Profit Maximization in Business
The speaker delves deeper into the application of derivatives for profit maximization in business. They discuss the cost function, which includes fixed and variable costs, and the revenue function, which depends on the quantity of goods sold and their price. The profit function is defined as the difference between revenue and cost. The goal is to find the quantity of goods that will maximize this profit. The paragraph explains how to analyze the slope of the tangent lines (the derivatives) of the revenue and cost functions to determine the optimal production level. An example with specific cost and revenue functions is used to illustrate the process, concluding with the calculation of the optimal number of items to produce for maximum profit.
🎨 Optimal Viewing Angles in Architecture
Shifting from economics to architecture, the speaker explores how to find the optimal viewing angle for a piece of art in a museum. They explain that standing too close to or too far from the artwork results in a small viewing angle, while the optimal distance maximizes the angle. The paragraph discusses the strategy of using calculus to find this distance by considering the tangent of the angles formed by the viewer's line of sight to the top and bottom of the artwork. The process involves setting up equations based on the geometry of the situation and using calculus to find the distance that maximizes the angle, thus providing the best view.
📚 Historical Challenge Problems in Calculus
This paragraph discusses historical challenge problems that were central to the development of calculus in the 17th century. The speaker mentions the catenary problem, which involves finding the shape of a hanging chain, and the brachistochrone problem, which is about finding the curve of fastest descent for a sliding object under gravity. The paragraph highlights the contributions of mathematicians like Galileo, Junius, Huygens, Johann Bernoulli, and Leibniz to these problems. It also touches on the properties of the catenary curve, such as its use in the design of the St. Louis Arch and its interesting characteristic related to square-wheeled bicycles.
🔍 The Catenary and Brachistochrone Problems
The speaker provides more details on the catenary and brachistochrone problems. They explain that the catenary curve is the shape formed by a hanging chain and that it has practical applications, such as in the construction of arches. The brachistochrone problem, posed by Johann Bernoulli, challenged mathematicians to find the curve that allows an object to slide down the fastest. The paragraph mentions that the solution to this problem was the cycloid curve, created by tracing a point on the rim of a rolling circle. The speaker also recounts the story of how Newton solved the brachistochrone problem and how his solution was recognized by Bernoulli.
🌐 Cycloid Curve and Dido's Problem
The paragraph continues the discussion on the cycloid curve, which is the solution to the brachistochrone problem. It explains that the cycloid curve allows a ball to reach the bottom faster than any other path when rolled down from a height. The speaker also introduces Dido's problem, an optimization problem from Virgil's Aeneid, where Queen Dido needed to enclose the maximum area with a fixed length of material. The paragraph suggests that the circle is the shape that maximizes the area, but it also hints at the complexity of proving this intuition using calculus, which is part of the field of calculus of variations.
🚀 Upcoming Lecture on Derivatives and Integrals
In the concluding paragraph, the speaker previews the next lecture, which will continue to explore the applications and variations of derivatives and integrals. They mention an upcoming discussion on flying objects, such as baseballs, indicating that the next lecture will delve into the physics of motion and how calculus is applied to understand and predict the trajectories of objects in flight.
Mindmap
Keywords
💡Optimization
💡Derivative
💡Profit
💡Marginal Cost and Marginal Revenue
💡Revenue Function
💡Cost Function
💡Catenary
💡Brachistochrone Problem
💡Cycloid
💡Calculus of Variations
Highlights
Introduction to optimization concepts using calculus in economics and architecture.
Explanation of profit maximization for a company by analyzing revenue and cost functions.
Derivative as a tool to find the rate of change in cost and revenue functions.
Definition and importance of marginal cost and marginal revenue in economic decision-making.
Graphical representation of revenue, cost, and profit functions to illustrate optimization.
Strategy to maximize profit by setting the derivative of revenue equal to the derivative of cost.
Example calculation to determine the optimal number of items to produce for maximum profit.
Transition to architectural optimization, specifically finding the best viewing angle for art in a museum.
Use of calculus to determine the optimal distance to stand from a painting to maximize viewing angle.
Introduction to the catenary curve, the shape of a hanging chain, and its unique properties.
Historical account of the catenary curve's discovery and its relevance to architecture.
Description of the brachistochrone problem and its significance in the history of calculus.
Solution to the brachistochrone problem involving the cycloid curve.
Demonstration of the cycloid's efficiency in a physical experiment comparing different paths.
Introduction to Dido's problem from Virgil's Aeneid, an optimization problem in land enclosure.
Overview of the calculus of variations as a field for solving complex optimization problems.
Anticipation of future lectures discussing derivatives, integrals, and the physics of flying objects.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: