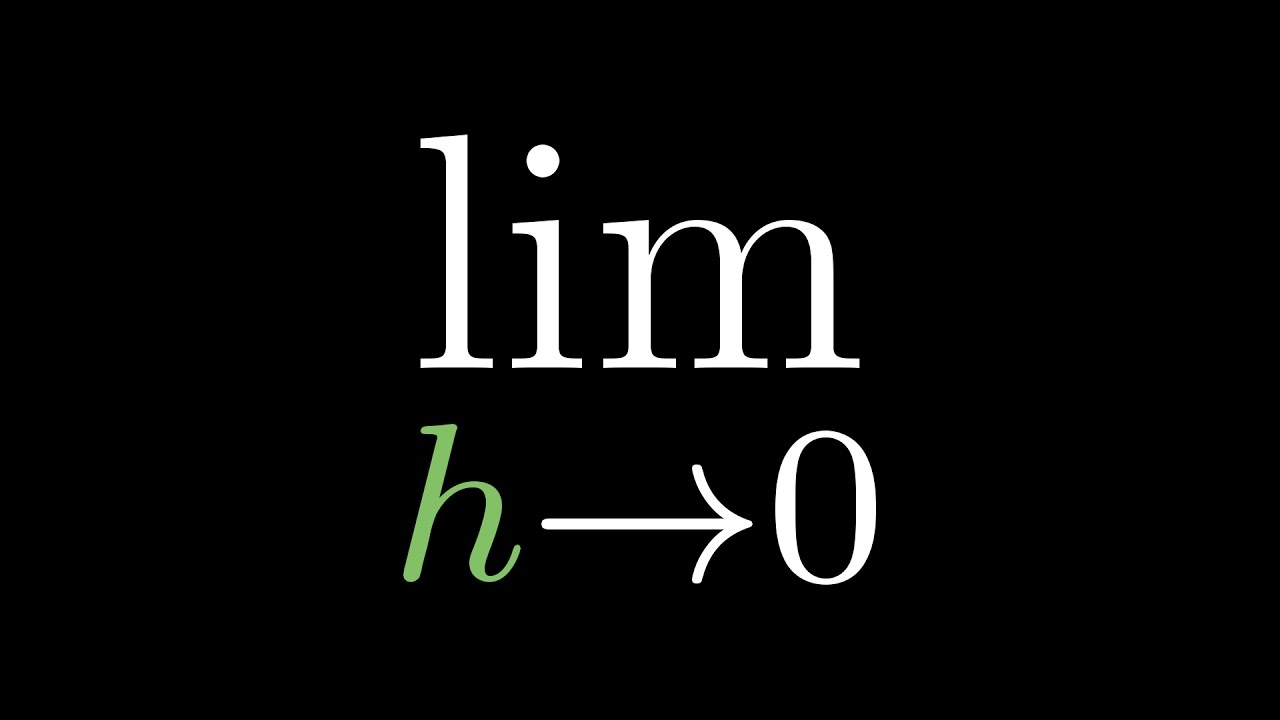Limits and Continuous Functions

MIT OpenCourseWare

15 Sept 201036:26

EducationalLearning

32 Likes 10 Comments

TLDRIn this educational video, Professor Gilbert Strang from MIT explores the concept of limits and continuity in functions. He uses intuitive explanations and visual representations to clarify what it means for a sequence or function to approach a limit, emphasizing the importance of understanding the behavior of functions as they near specific values. Strang also discusses the 'risky' cases where limits might not exist or are indeterminate, such as 0/0 or infinity/infinity, and introduces L'Hôpital's Rule as a method to tackle certain indeterminate forms. The video concludes with the formal definition of a continuous function using epsilon-delta logic, illustrating the historical significance and complexity of this fundamental calculus topic.

Takeaways

📚 The script discusses the concept of limits in sequences and functions, emphasizing the idea that the first few numbers in a sequence do not affect its limit.
🔍 It explains that for a sequence to approach a limit 'A', the terms must eventually fall within an arbitrarily small interval around 'A' and stay within it as the sequence progresses.
🌟 The script highlights three possible limits for a sequence: infinity, a positive number, or zero, but also notes that many sequences may not have a limit at all, such as sine(n) or cosine(n).
❓ The importance of questioning the behavior of limits is underscored, as mathematicians often look for special or unusual cases where limits might not behave as expected.
🚫 The script identifies 'dangerous' cases for limits, such as when both sequences approach infinity, where the result of operations like subtraction or division can be indeterminate.
🤔 It poses questions about the behavior of limits under different operations, such as addition, multiplication, and division, and emphasizes the uncertainty in cases like 'infinity minus infinity' or '0 over 0'.
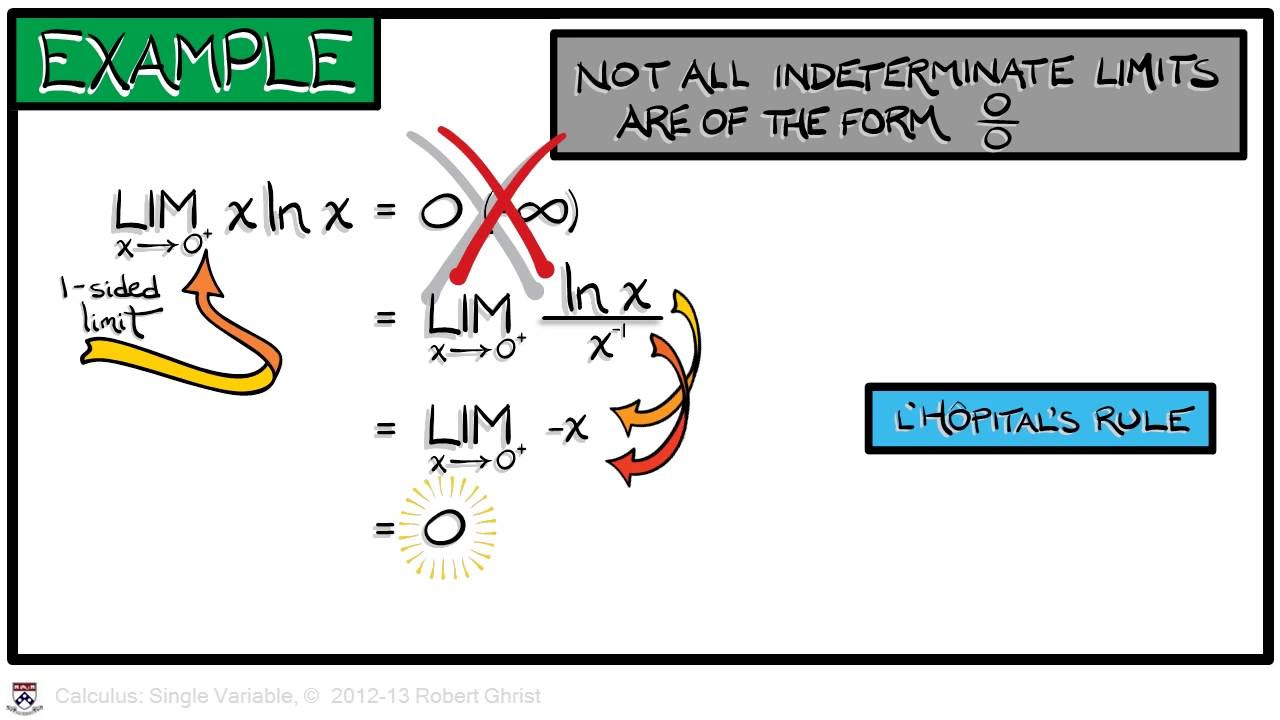
📉 The concept of L'Hopital's rule is introduced as a method to determine limits of the form '0/0' or 'infinity/infinity' by considering the slopes of the functions involved.
📈 The script differentiates between a function having a defined slope and being continuous, noting that a function can be continuous even if its slope is not defined, as in the case of the square root function at x=0.
🛑 The formal definition of a continuous function is presented, involving the idea of epsilon and delta, and the necessity for a function to stay within a given band around a point as it approaches that point.
🚫 An example of a discontinuous function is given, where the sine of 1/x does not stay within any band as x approaches 0, illustrating the oscillation and divergence of the function.
🔑 The takeaways from the script highlight the nuanced understanding required for limits and continuity, the potential pitfalls in assuming behavior, and the mathematical tools and concepts used to analyze them.

Q & A

What is the basic idea of a limit in mathematics?
-The basic idea of a limit is to determine what a sequence of numbers approaches as the sequence progresses. Specifically, for a sequence to approach a limit A, the numbers must eventually get close to A and stay within any arbitrarily small interval around A.
What does it mean for a sequence to approach a number, such as 7?
-For a sequence to approach 7, the numbers in the sequence must get closer and closer to 7 and stay within any chosen small interval around 7 as the sequence progresses.
What are the possible limits for a sequence?
-The possible limits for a sequence are any positive number, zero, and infinity. However, many sequences do not have limits at all, such as the sine or cosine of n.
What is an example of a sequence where the limit is infinity?
-A sequence has a limit of infinity if the numbers in the sequence eventually become larger than any arbitrarily large number and stay there.
Why is the concept of 0/0 considered dangerous in calculus?
-The concept of 0/0 is dangerous because it is indeterminate; the limit depends on the rate at which both the numerator and the denominator approach zero. This can result in a variety of outcomes, making it impossible to determine the limit without additional information.
What is L'Hopital's rule and when is it used?
-L'Hopital's rule is a method used to evaluate limits of indeterminate forms like 0/0 or infinity/infinity. It states that if the limits of the functions in the numerator and denominator both approach zero or infinity, the limit of the quotient can be found by taking the limit of the quotient of their derivatives.
What is the definition of a continuous function?
-A function is continuous at a point a if the function's value at that point equals the limit of the function as x approaches a. In other words, f(x) approaches f(a) as x approaches a.
What is an example of a function that is not continuous?
-The function sine(1/x) as x approaches 0 is not continuous because the oscillations of the sine function increase without bound as x gets closer to 0, making it impossible to stay within any fixed interval around a single value.
What does the epsilon-delta definition of continuity state?
-The epsilon-delta definition of continuity states that for every epsilon greater than zero, there exists a delta greater than zero such that if the distance between x and a is less than delta, the distance between f(x) and f(a) is less than epsilon.
Why is the slope of the square root function at x=0 considered infinite?
-The slope of the square root function at x=0 is considered infinite because the derivative of the square root function, which is 1/(2*sqrt(x)), becomes unbounded as x approaches 0, leading to a vertical tangent line at the origin.

Outlines

00:00

📊 Introduction to Limits and Continuity

The professor introduces the concept of limits and continuity, using a visual approach to explain how a sequence of numbers approaches a limit. He explains the behavior of numbers approaching a specific value, zero, or infinity, emphasizing the importance of understanding limits in mathematical analysis.

05:01

🔍 Analyzing Limits with Examples

The professor discusses potential pitfalls in limit calculations, particularly when dealing with expressions like infinity minus infinity or zero times infinity. He uses examples to show how different sequences can produce varied outcomes, highlighting the need for careful consideration in mathematical analysis.

10:04

⚖️ The Challenge of Division in Limits

The focus shifts to division in limit calculations, with particular attention to cases where both numerator and denominator approach zero. The professor explains how the behavior of sequences determines the limit, and introduces L'Hopital's rule as a method to resolve indeterminate forms by comparing the rates at which functions approach zero.

15:06

📈 Continuity and Its Importance

The professor elaborates on the concept of continuity in functions, explaining that a function is continuous if it can be drawn without lifting the pen. He introduces the formal definition involving epsilon and delta, and uses examples to show how continuous functions behave near specific points, even when slopes are not defined.

20:06

🧮 Practical Examples of Continuity

Further examples are provided to illustrate continuity, including cases where functions have infinite slopes. The professor explains that despite infinite slopes, functions can still be continuous if they meet the epsilon-delta criterion. He underscores the distinction between continuity and having a well-defined slope.

25:07

🌉 Visualizing Continuity with Graphs

Graphical representations are used to explain continuous functions. The professor demonstrates how a function that approaches a value smoothly can still be continuous even if it has an infinite slope at a point. He stresses the importance of understanding how functions behave as they approach specific points.

30:09

📐 The Epsilon-Delta Definition of Continuity

The professor delves into the epsilon-delta definition of continuity, explaining the logic behind choosing bands around function values and points. He uses a narrative involving Socrates and Plato to illustrate how functions must stay within defined bands to be considered continuous.

35:17

🚫 Example of Discontinuity

An example of a discontinuous function is presented with the sine of 1 over x as x approaches zero. The professor explains how this function fails to stay within any epsilon band, demonstrating discontinuity. He contrasts this with modified functions that restore continuity.

Mindmap

Keywords

💡Limit

A limit in mathematics, particularly in calculus, refers to the value that a function or sequence 'approaches' as the input (often denoted as 'x') approaches some value (often denoted as 'a'). The concept is central to understanding continuity and differentiability. In the video, the professor illustrates the idea of limits with sequences and functions, using the example of a sequence approaching a number like 7 or infinity to explain the concept intuitively.

💡Continuous Function

A continuous function is one where there are no abrupt changes in value, meaning that it can be drawn without lifting the pen from the paper. It is a fundamental concept in calculus, closely related to the idea of a function having a limit at every point in its domain. The video discusses the properties of continuous functions and provides examples, such as the function approaching a limit as x approaches a specific value.

💡Epsilon (ε)

Epsilon is a small, positive number often used to describe an arbitrarily small positive distance in mathematical definitions, particularly in limits and continuity. In the video, epsilon is used to define the 'band' or 'strip' around a number where the function's value must lie to be considered close to another value, illustrating the precision needed for a function to be continuous.

💡Delta (Δ)

Delta, another Greek letter used in calculus, represents a small change in the input of a function. It is used in conjunction with epsilon to define continuity formally. In the video, delta is introduced as the 'vertical band' chosen by 'Plato' to ensure that for any epsilon 'band' chosen by 'Socrates', the function's value stays within the epsilon band when the input is within the delta band.

💡Infinity

Infinity is not a number but rather a concept representing an unbounded quantity. In the context of limits, it describes a situation where a function or sequence does not approach a finite number but rather increases without bound. The video discusses the concept of infinity in relation to limits, such as when a sequence of numbers 'approaches infinity'.

💡Sequence

A sequence is an ordered list of numbers, which can be finite or infinite. In the video, sequences are used to illustrate the concept of limits, showing how a sequence of numbers might approach a certain value or infinity as the sequence progresses.

💡Derivative

The derivative of a function at a certain point is a measure of the rate at which the function's value changes with respect to changes in its input. It is a fundamental concept in calculus and is related to the slope of the function's graph. In the video, the concept of derivatives is introduced in the context of L'Hôpital's rule, which involves taking derivatives to evaluate limits involving indeterminate forms like 0/0 or ∞/∞.

💡Indeterminate Form

An indeterminate form is a result that does not provide a specific value and typically arises when simplifying the limit of a function that results in 0/0, ∞/∞, 0·∞, 1^∞, or ∞ - ∞. In the video, the professor discusses indeterminate forms as situations where the direct calculation of a limit is not immediately clear and additional methods, like L'Hôpital's rule, are needed.

💡L'Hôpital's Rule

L'Hôpital's rule is a method in calculus for finding the limit of a function in cases where the direct application of limit definitions results in an indeterminate form. It states that if the limit of the ratio of two functions results in an indeterminate form, then this limit is equal to the limit of the ratio of their derivatives, provided the latter exists. The video explains L'Hôpital's rule as a strategy to deal with tricky limits involving 0/0 or ∞/∞.

💡Slope

In the context of functions, the slope refers to the steepness or gradient of the function's graph. It is a measure of how much the function's value changes with respect to changes in the input. In the video, the professor uses the concept of slope to explain how the behavior of a function near a certain point can be understood, especially when discussing continuity and the approach to limits.

Highlights

Introduction to the concept of limits in sequences and functions without using formal definitions.

Explanation of what it means for a sequence to approach a limit, using the analogy of a 'slit' that numbers must eventually stay within.

Clarification that the first few numbers in a sequence do not affect the limit.

Discussion on the behavior of sequences approaching infinity and the concept of epsilon.

Introduction of the idea of limits for multiplication and division of sequences, including the indeterminate forms of 0/0 and ∞/∞.

Highlighting the potential pitfalls in determining limits, especially when dealing with infinity.

Use of L'Hopital's rule to resolve indeterminate forms like 0/0 by considering the slopes of the functions involved.

Illustration of the difference between a function with a defined slope and one with an infinite slope at a certain point.

Differentiation between a function being continuous and having a well-defined slope.

Definition of a continuous function in terms of approaching a value as x approaches a specific point.

The epsilon-delta definition of continuity, explaining the relationship between vertical and horizontal 'bands' around a point.

Examples demonstrating the difference between functions that are continuous and those that are not, using sine functions as an example.

The importance of understanding the behavior of functions near a point to determine continuity.

The historical significance of the development of the concept of continuity and its impact on calculus.

The practical application of the epsilon-delta definition in determining the continuity of functions.

The role of examples in understanding the theoretical concepts of limits and continuity.

The presentation of MIT OpenCourseWare and Gilbert Strang, along with a call for donations to support free and open access to MIT courses.

Transcripts

Browse More Related Video

Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus

Limits via Graphs!

Using L'Hopital's Rule to show that exponentials dominate polynomials

Calculus Chapter 1 Lecture 8 l'Hopital's Rule

Challenging Limits from Graphs

Calculus Chapter 1 Lecture 7 Limits

Related Tags

Limits Continuous Functions Mathematics Calculus Learning Concepts Examples Educational MIT Lecture