Differentiability of Piecewise Functions - Calculus
TLDRIn this educational video, Van demonstrates three methods to determine the differentiability of piecewise functions. He starts with a visual approach, identifying non-differentiability at sharp turns, then moves to algebraic techniques involving derivatives and absolute value properties. Finally, he discusses the limit definition, emphasizing the importance of checking continuity before differentiability. The video includes examples to illustrate each method, highlighting potential pitfalls and the significance of proper analysis in mathematical functions.
Takeaways
- 📚 The video discusses methods to determine the differentiability of piecewise functions.
- 🎨 The first example uses graphing to identify non-differentiability at a sharp turn in the function's graph.
- 🔍 An alternative method involves rewriting the absolute value function to facilitate derivative calculation.
- 📐 The chain rule is applied to find the derivative of the rewritten function, leading to the conclusion of non-differentiability at a specific point.
- 🚫 The domain of the derivative function must be checked for forbidden values that cause the denominator to be zero.
- 🤔 The limit definition of differentiability is explored as a more complex approach, requiring the evaluation of left and right side limits.
- 🔄 The video emphasizes the importance of checking for continuity before attempting to prove differentiability.
- 📉 For the second example, continuity and differentiability are proven by comparing left and right side limits and the function value at a critical point.
- 📈 The derivative of each piece of the function is calculated to check for differentiability, ensuring the left and right limits match the derivative.
- ❗ The video warns against prematurely concluding differentiability without first confirming continuity.
- 🚫 The final example demonstrates a common mistake of assuming differentiability without verifying continuity, highlighting the importance of a thorough approach.
Q & A
What is the easiest way to determine if a piecewise function is differentiable according to Van?
-The easiest way to determine if a piecewise function is differentiable, as suggested by Van, is to sketch the graph of the function. If there is a sharp turn or a discontinuity at a certain point, the function is not differentiable at that point.
Why is the function with the absolute value of x minus four not differentiable at x equals four?
-The function with the absolute value of x minus four is not differentiable at x equals four because the graph has a sharp 'V' shape at this point, indicating a discontinuity in the derivative.
What is an alternative method to determine differentiability without graphing the function?
-An alternative method is to use the definition of absolute value, rewriting the function in terms of square roots and then applying the chain rule to find the derivative. If the derivative simplifies to a form that does not have a discontinuity, it can help determine differentiability.
How does the derivative of the absolute value function relate to the original function?
-The derivative of the absolute value function, f'(x), is related to the original function by being the ratio of x - 4 over the absolute value of x - 4, which helps in determining the differentiability of the function at x = 4.
What is the significance of checking the domain of f'(x) when determining differentiability?
-Checking the domain of f'(x) is important because it reveals any values of x that would make the denominator of the derivative equal to zero, which would indicate points where the function is not differentiable.
How does Van suggest using the limit definition to determine differentiability?
-Van suggests using the limit definition by finding the limit as x approaches a certain point of (f(x) - f(a)) / (x - a). If this limit does not exist, the function is not differentiable at that point.
Why is it important to first show that a function is continuous before proving differentiability?
-It is important to first show that a function is continuous because a function must be continuous at a point to be differentiable at that point. Discontinuity automatically disqualifies a function from being differentiable.
What is the process to show that a piecewise function is continuous at a certain point?
-To show that a piecewise function is continuous at a certain point, one must check if the left and right limits at that point are equal to each other and to the function value at that point.
How does the derivative of a piecewise function affect its differentiability?
-The derivative of a piecewise function must be evaluated term by term, and the left and right limits of the derivative at points of interest must be equal for the function to be differentiable at those points.
What is the common mistake that students make when trying to determine differentiability without checking for continuity first?
-The common mistake is to rush into finding the derivative of each piece of the function and checking the limits of the derivative without first ensuring the function is continuous. Continuity must be established before differentiability can be considered.
Why is the function h(x) not differentiable at x equals one according to the script?
-The function h(x) is not differentiable at x equals one because it is not continuous at that point. The left and right limits of h(x) as x approaches one are not equal, indicating a discontinuity.
Outlines
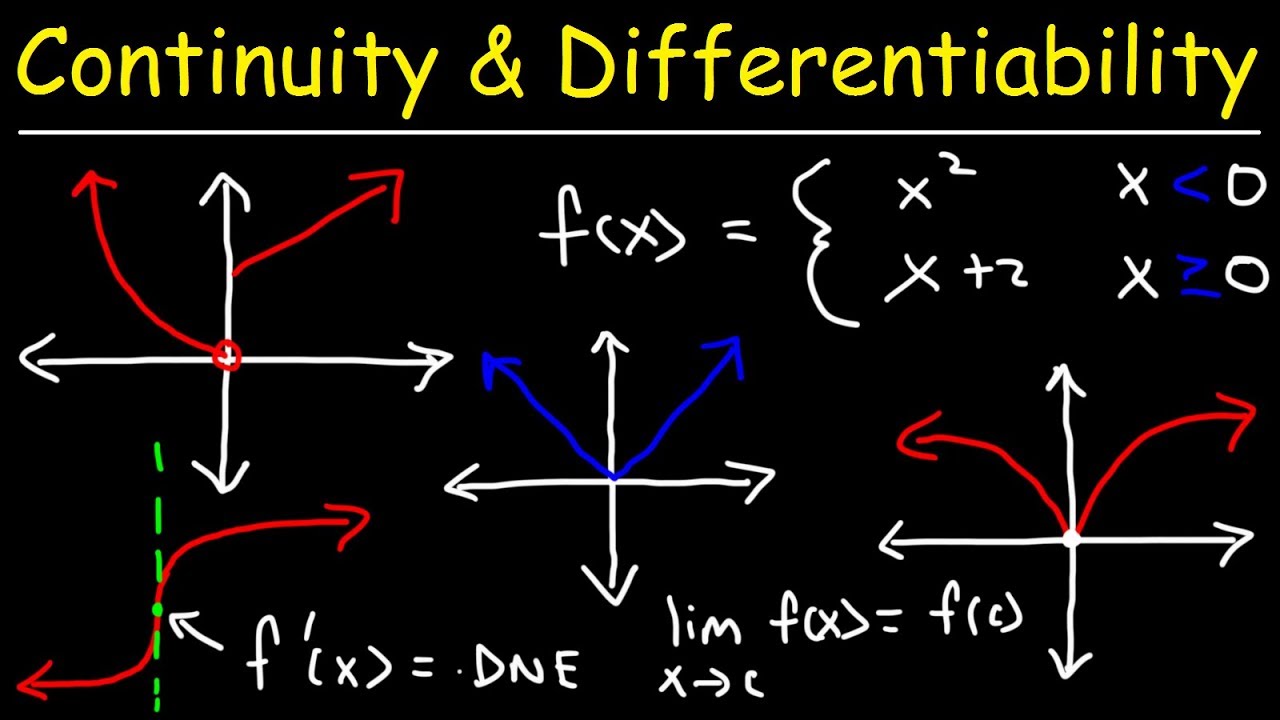
📚 Understanding Differentiability of Piecewise Functions
Van introduces the concept of differentiability for piecewise functions, focusing on three examples. He explains that the first function, involving the absolute value of x minus four, is not differentiable at x equals four due to its V-shape graph. He then suggests an alternate method using the definition of absolute value and the chain rule to find the derivative. The derivative simplifies to x minus four over the absolute value of x minus four. Van also points out that the domain of the derivative function is restricted at x equals four, which supports the non-differentiability at that point. Lastly, he mentions the limit definition as a more complex approach to determine differentiability, which in this case also shows the function is not differentiable at x equals four.
🔍 Demonstrating Continuity and Differentiability
In the second paragraph, Van demonstrates how to show a piecewise function is continuous and then differentiable. He uses the function g(x) as an example, showing that the left and right limits at x equals two are equal to the function value at that point, confirming continuity. He then proceeds to find the derivative of each piece of the function and checks the left and right limits of the derivative at x equals two, finding them to be equal, which confirms differentiability at that point. Van emphasizes the importance of first establishing continuity before checking for differentiability.
⚠️ The Pitfall of Skipping Continuity Checks
The final paragraph serves as a cautionary tale about the importance of checking for continuity before attempting to prove differentiability. Van uses the function h(x) to illustrate a common mistake where a student might incorrectly assume differentiability by only checking the derivative's left and right limits. However, upon closer inspection, the function is found to be discontinuous at x equals one, as the left and right limits do not match. This discontinuity automatically disqualifies the function from being differentiable at that point, highlighting the necessity of a thorough analysis before concluding differentiability.
📢 Closing Remarks and Call to Action
Van concludes the video with a call to action, encouraging viewers to like and subscribe to support the channel's growth. He also invites viewers to leave comments with topic requests for future videos, expressing gratitude for the audience's engagement.
Mindmap
Keywords
💡Differentiable
💡Piecewise function
💡Absolute value
💡Derivative
💡Continuity
💡Limit
💡Chain rule
💡Domain
💡Graphical analysis
💡Slope
Highlights
Introduction to determining the differentiability of piecewise functions with three examples.
The first example involves a function with an absolute value, which is not differentiable at a sharp turn at x=4.
An alternate method for finding the derivative of an absolute value function using the square root definition.
Deriving the function using the chain rule and simplifying to find the derivative of the absolute value function.
Explaining the domain of the derivative and identifying the point where the original function is not differentiable.
Using the limit definition to determine differentiability, with the example of a function not differentiable at x=4.
The importance of checking continuity before determining differentiability, demonstrated with the second example.
Showing that a piecewise function is continuous by comparing left and right side limits at a critical point.
Differentiability is confirmed when the left and right limits of the derivative match at a critical point.
A cautionary note about not rushing to check differentiability without first ensuring continuity.
The third example demonstrates a common mistake in assuming differentiability without checking continuity.
Identifying the lack of continuity in the third example by comparing left and right side limits.
The automatic disqualification of differentiability when a function is not continuous.
The three conditions for continuity: existence of the limit, function definition, and equality of limit and function value.
Conclusion of the video with a summary of the process for determining the differentiability of piecewise functions.
Encouragement for viewers to like, subscribe, and leave comments for further content requests.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: