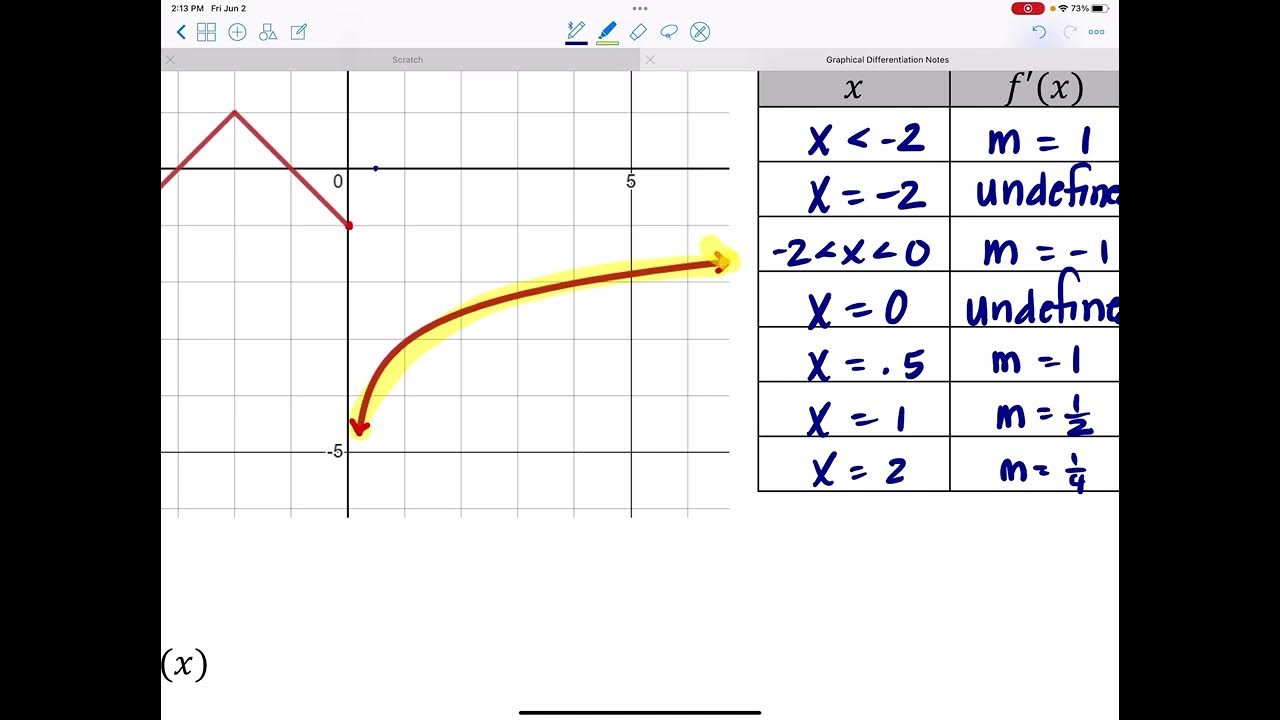
Screencast 1.7.4: Determining differentiability graphically

GVSUmath
31 Jul 201304:41
EducationalLearning
32 Likes 10 Comments

TLDRThis screencast teaches viewers to identify differentiability of a function by its graph. A function is differentiable at a point if it appears locally linear upon zooming in, allowing a tangent line with a well-defined slope. The video demonstrates this concept using a graph without a formula, highlighting points where the function is differentiable due to linearity and points where it is not, such as at discontinuities, jumps, or sharp corners, which prevent the function from being locally linear.

Takeaways
  • 📚 A function is differentiable at a point x=a if its derivative exists at that point.
  • 📈 Graphically, differentiability implies that a tangent line with a well-defined slope can be drawn to the graph at x=a.
  • 🔍 When zooming in on a graph at a certain point, if it appears as a single straight line, the function is locally linear and thus differentiable there.
  • 👀 The script uses a visual approach to determine differentiability by examining the graph of a function without a formula.
  • 📍 At x=1, the function appears locally linear upon zooming, indicating differentiability despite slight curvature.
  • 📉 At x=2, the graph looks like a single straight line upon zooming, confirming differentiability.
  • 🚫 At x=4, the function is not differentiable because it does not exist at that point, represented by a hollow circle.
  • 🔗 At x=6, the function is not differentiable due to a jump in the graph, preventing the appearance of a single straight line upon zooming.
  • ⚠️ At x=8, the function has a corner or cusp, which means it is not locally linear and hence not differentiable.
  • 🛑 The function is not differentiable at specific points where the graph breaks, jumps, or forms a corner.
  • 🔑 Differentiability can be visually assessed by checking if the graph is locally linear at a given point when zoomed in.
Q & A

  • What does it mean for a function to be differentiable at a point?

    -A function is differentiable at a point x=a if the derivative of the function at that point exists, which graphically means that a tangent line with a well-defined slope can be drawn to the graph of the function at x=a.

  • How can you determine if a function is differentiable by looking at its graph?

    -You can determine if a function is differentiable by zooming in on the graph at a specific point. If the graph appears to be a single straight line upon zooming in, then the function is locally linear at that point and is differentiable there.

  • What does the presence of a hollow circle on the graph of a function signify?

    -A hollow circle on the graph of a function signifies that the function does not exist at that point, which means it is not differentiable at that point because there is no graph to which a tangent line can be attached.

  • Why is the function not differentiable at x=4 in the given example?

    -The function is not differentiable at x=4 because the graph has a break at that point, represented by a hollow circle. Upon zooming in, it would not appear as a straight line but rather a line with a break, indicating the function is not locally linear there.

  • What is the graphical representation of a function being differentiable at x=6?

    -At x=6, the function is not differentiable because there is a jump in the graph, which prevents the appearance of a single straight line upon zooming in. The presence of multiple line segments instead of a single unbroken line indicates non-differentiability.

  • What is the significance of a sharp corner or cusp on the graph of a function?

    -A sharp corner or cusp on the graph of a function indicates that the function is not differentiable at that point. No matter how much you zoom in, the corner remains, and the function does not appear locally linear, preventing the drawing of a tangent line.

  • Why is the function differentiable at x=1 according to the script?

    -The function is differentiable at x=1 because, upon zooming in on that portion of the graph, it appears locally linear, even though there is a slight curvature. The more you zoom in, the straighter it looks, indicating the presence of a well-defined tangent line.

  • What is the condition for a function to be differentiable at x=2 in the script's example?

    -The function is differentiable at x=2 because when you zoom in on the graph at that point, it looks like a single straight line, allowing for the drawing of a tangent line and indicating differentiability.

  • What is the term used in the script to describe a function that appears as a straight line when zoomed in at a certain point?

    -The term used in the script to describe this property is 'locally linear,' which is a condition for differentiability at a point.

  • Can a function be differentiable at a point where its graph has a sharp turn?

    -No, a function cannot be differentiable at a point where its graph has a sharp turn or corner. The function must be locally linear, which a sharp turn does not satisfy, thus preventing the drawing of a tangent line.

  • What is the conclusion about the differentiability of the function f in the script?

    -The conclusion is that the function f is not differentiable at three points: x=4, x=6, and x=8. It is differentiable everywhere else, as the graph appears locally linear upon zooming in at any other point.

Outlines
00:00
📈 Understanding Differentiability Through Graph Analysis

This paragraph introduces the concept of differentiability in functions using a graphical approach. It explains that a function is differentiable at a point if its derivative exists at that point, which graphically means that a tangent line with a well-defined slope can be drawn. The function's graph should appear as a single straight line when zoomed in at the point of interest. The script uses an unnamed function 'f' to illustrate this by identifying points where the function is locally linear and thus differentiable, such as at x=1 and x=2, and points where it is not, such as at x=4, x=6, and x=8, due to the absence of the function, jumps, or corners in the graph.

Mindmap
Keywords
💡Differentiable
Differentiable refers to a property of a function where it has a derivative at a certain point. In the context of the video, a function is differentiable at a point x=a if the derivative exists, which graphically means that a tangent line with a well-defined slope can be drawn to the graph at that point. The script uses the graph of a function to illustrate where it is differentiable, such as at x=1 and x=2, where the graph appears to be locally linear upon zooming in.
💡Derivative
The derivative of a function at a given point is a measure of the rate at which the function changes at that point. It is a fundamental concept in calculus and is related to the slope of the tangent line to the function's graph. In the video, the existence of a derivative is what makes a function differentiable, as seen in the discussion of the function being differentiable at x=1 and x=2.
💡Tangent Line
A tangent line is a straight line that touches a curve at a single point without crossing it. It represents the linear approximation of the function at that point. The script explains that if a function is differentiable at a point, one should be able to draw a tangent line to the graph at that point, indicating a well-defined slope.
💡Locally Linear
Locally linear means that in the vicinity of a certain point, the function's graph appears to be a straight line. The script uses this term to describe the property of a function's graph when it is differentiable. For example, when zooming in on the graph at x=1, the function appears to be locally linear, suggesting differentiability.
💡Zoom In
Zooming in is the action of focusing on a specific part of a graph to examine it more closely. In the script, zooming in is used as a method to determine if the function's graph appears linear at a certain point, which is a criterion for differentiability.
💡Hollow Circle
In the context of the script, a hollow circle on the graph represents a point where the function does not exist. The script mentions x=4 as an example where the function is not differentiable because the graph has a hollow circle, indicating a discontinuity.
💡Discontinuity
Discontinuity refers to a point on the graph of a function where the function is not defined or the limit does not exist. The script uses the hollow circle at x=4 to illustrate a point of discontinuity, which is why the function is not differentiable at that point.
💡Jump
A jump in the context of the script refers to a sudden change or discontinuity in the graph of a function. For instance, at x=6, the graph has a jump, which prevents the function from being differentiable at that point because zooming in would not result in a single straight line.
💡Corner or Cusp
A corner or cusp on a graph is a point where the function changes direction abruptly, forming a sharp angle. The script points out x=8 as an example where the function has a corner, which means it is not locally linear and hence not differentiable at that point.
💡Non-Differentiable Points
Non-differentiable points are the specific locations on the graph of a function where the function is not differentiable. The script identifies x=4, x=6, and x=8 as non-differentiable points because at these points, the graph does not appear locally linear upon zooming in.
💡Local Linearity
Local linearity is the property of a function's graph that appears as a straight line in the vicinity of a point. The script emphasizes that for a function to be differentiable at a point, it must exhibit local linearity, as seen in the discussion of the function being differentiable at x=1 and x=2.
Highlights

A function is differentiable at a point if the derivative exists and a tangent line can be drawn with a well-defined slope.

Differentiability implies the graph appears as a single straight line when zoomed in at a specific point.

The function f is represented graphically without a formula, focusing on differentiability through visual analysis.

At x equals 1, the function appears locally linear and thus is differentiable despite slight curvature.

The graph's locally linear appearance at x equals 2 indicates differentiability.

Non-differentiability at x equals 4 due to the function's non-existence, represented by a hollow circle.

A hollow circle suggests a break in the graph, preventing the function from being locally linear and differentiable.

At x equals 6, a jump in the graph signifies non-differentiability as it does not form a single straight line upon zooming.

Non-differentiability at x equals 8 is due to a sharp corner or cusp, which does not allow a tangent line to be drawn.

The function f is not differentiable at x equals 4, 6, and 8, but differentiable everywhere else.

Differentiability can be visually determined by the graph's locally linear appearance upon zooming in at any given point.

The screencast provides a conceptual visual method to assess a function's differentiability from its graph.

Differentiability implies the absence of breaks, jumps, or corners in the graph at the point of interest.

A tangent line's inability to be drawn at a point indicates the function is not differentiable there.

The function's graph must appear as an unbroken straight line to be considered differentiable at a point.

Zooming in on the graph is a practical way to visually confirm differentiability by checking for a single straight line.

The screencast concludes with a summary of the visual criteria for differentiability from a graph.

Transcripts

Browse More Related Video

BusCalc 16 Continuity and Differentiability

Linear Approximations | Using Tangent Lines to Approximate Functions

Calculus 1 Lecture 3.2: A BRIEF Discussion of Rolle's Theorem and Mean-Value Theorem.

Graphical Differentiation

1.4 - Differentiation Using Limits of Difference Quotients

Mean Value Theorem

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DifferentiabilityFunction GraphsLocal LinearityDerivativeTangent LineZoom InNon-DifferentiableCusp PointJump DiscontinuityMath ConceptsEducational Content