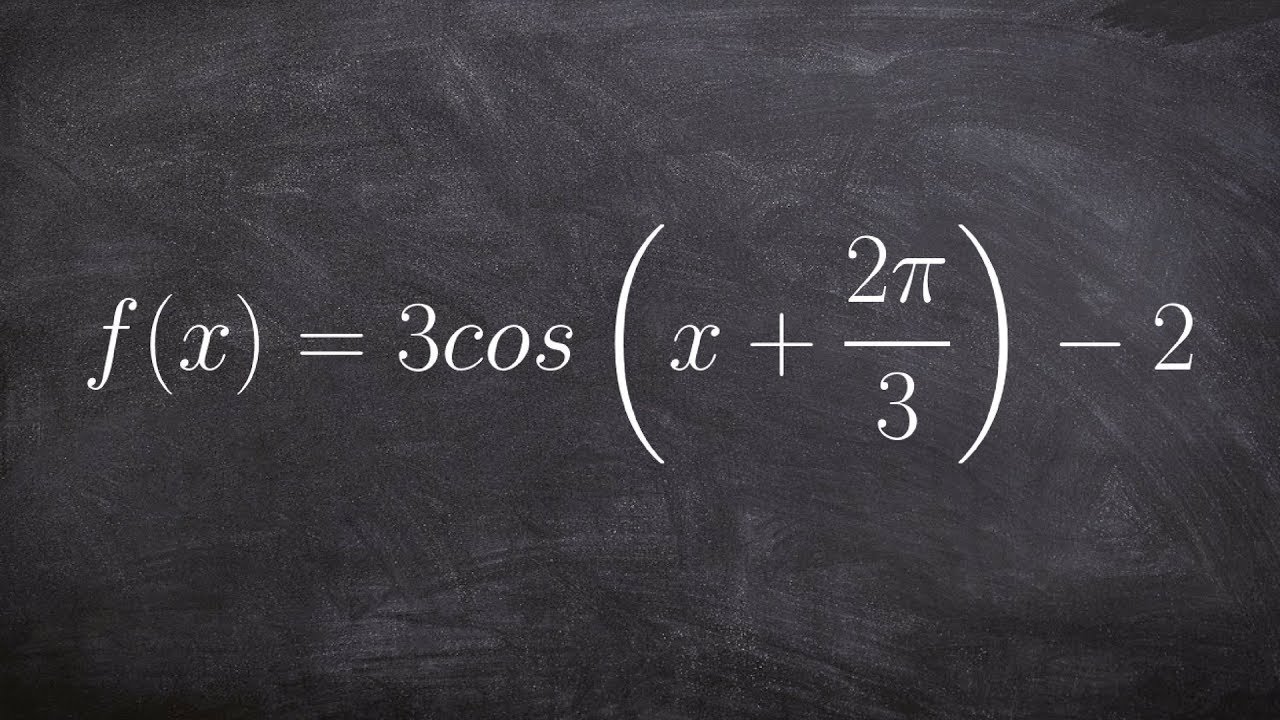MCR3U UNIT 5 Writing Sine Cosine Equation Given Graph

Learning with Lee
13 May 201409:08
EducationalLearning
32 Likes 10 Comments

TLDRThis lesson teaches how to derive the equations for sine and cosine functions by analyzing a given graph. The instructor identifies key features such as crests at 5, minimums at -3, and the axis at y=1, leading to an amplitude of 4. The period is determined to be 180 degrees by examining points on the graph. Using this information, the K value is calculated as 2. The lesson demonstrates how to write equations for both sine and cosine functions, accounting for amplitude, period, phase shift, and vertical shift, with examples provided for each.

Takeaways
  • πŸ“š The lesson's objective is to derive the equation for a sine or cosine function from a given graph.
  • πŸ” The graph's maximum points, or crests, are at 5, indicating a key feature for determining the amplitude.
  • πŸ“‰ The minimum points, or troughs, are at -3, -2, and -1, which helps calculate the total distance from maximum to minimum.
  • πŸ“ The axis of the curve is midway between the crests and troughs, found to be at y = 1.
  • πŸ“ The amplitude is the distance from the axis to the peak or trough, calculated to be 4 units.
  • πŸ” The period of the function is determined by the distance between two crests or troughs, found to be 180 degrees.
  • πŸ”’ The K value, which relates to the period, is calculated to be 2 by fitting two complete cycles within 360 degrees.
  • πŸ“ˆ The sine function starts on the axis and has a phase shift of 45 degrees to the right.
  • πŸ“‰ The cosine function aligns with the zero point on the graph, indicating no phase shift and a direct match with the sine function's parameters except for the phase shift.
  • πŸ’‘ The equation for the sine function includes a negative amplitude due to its downward opening, a phase shift of -45 degrees, a period determined by K=2, and an axis of y=1.
  • πŸ“ The equation for the cosine function mirrors the sine function's parameters but without the negative amplitude and phase shift, maintaining the same axis of y=1.
Q & A

  • What is the main objective of the lesson in the provided transcript?

    -The main objective of the lesson is to write the equation for a sine function and a cosine function that models the graph presented in the lesson.

  • What is the first step in analyzing the graph to determine the equation of the sine or cosine function?

    -The first step is to identify the maximum points (crests) and minimum points (troughs) of the graph to determine the amplitude and the axis of the curve.

  • What is the amplitude of the graph in the lesson?

    -The amplitude of the graph is four, which is the distance from the axis of the curve to either a maximum peak or a minimum trough.

  • How is the axis of the curve determined from the maximum and minimum points?

    -The axis of the curve is determined to be exactly halfway between the crests and troughs, which in this case is at y equals one.

  • What is the total distance between the maximum and minimum points on the graph?

    -The total distance between the maximum point at 5 and the minimum point at -3 is eight.

  • What is the period of the sine curve in the lesson?

    -The period of the sine curve is 180, which is the distance between two crests or two troughs.

  • How can you determine the value of 'K' for the sine or cosine function?

    -The value of 'K' can be determined by dividing 360 by the observed period length, which in this case gives a 'K' value of two.

  • What is the significance of the phase shift in the sine function equation?

    -The phase shift indicates how much the sine function has been moved to the left or right on the graph. In the lesson, the sine function has been pushed over by 45 degrees.

  • How does the reflection of the sine function affect its equation in the lesson?

    -The reflection of the sine function, which causes it to open downwards instead of upwards, is indicated by a negative sign in front of the sine function in the equation.

  • What is the equation of the sine function if it is pushed over by 45 degrees and opens downwards?

    -The equation of the sine function in this case would be y = -4 * sin(2 * (theta - 45)) + 1.

  • What would be the equation of the cosine function for the given graph?

    -The equation of the cosine function for the given graph would be y = 4 * cos(2 * theta + 1), assuming no phase shift and the same amplitude and axis as the sine function.

Outlines
00:00
πŸ“š Analyzing Graph to Determine Sine and Cosine Equations

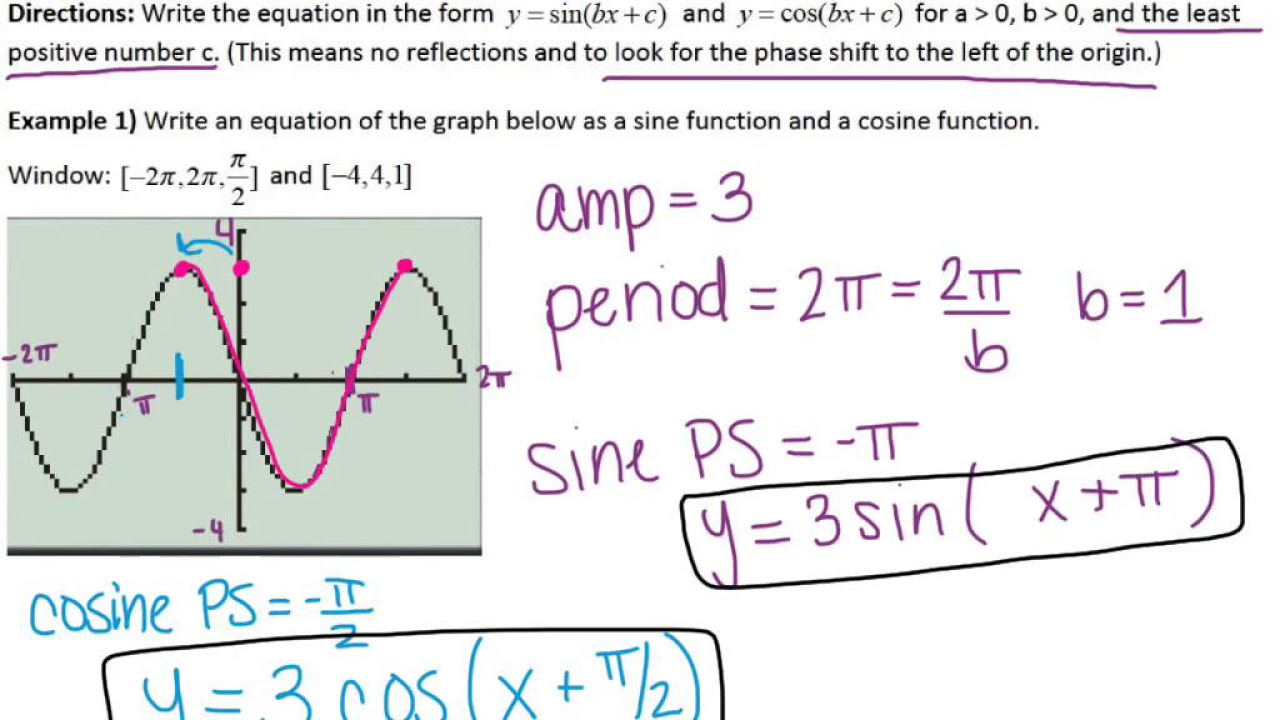
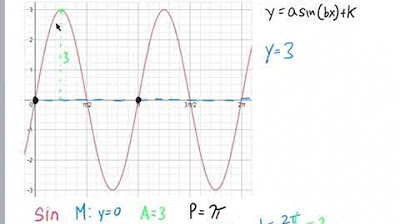
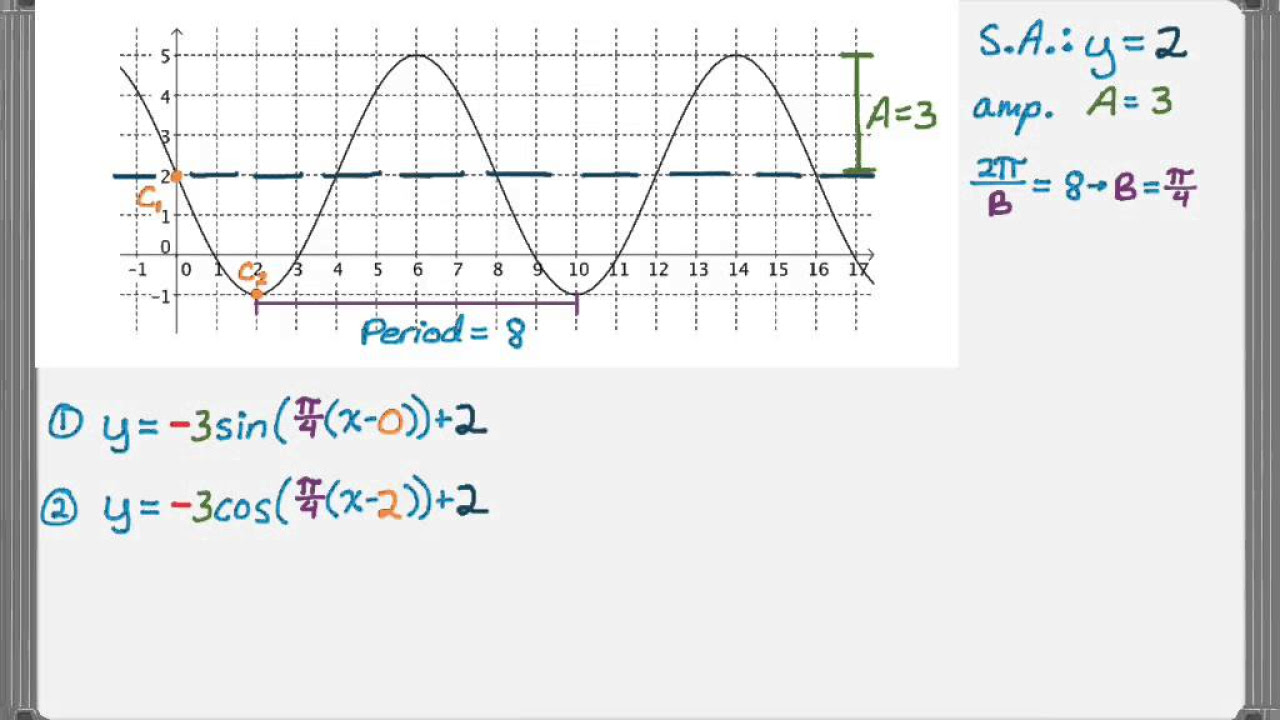
This paragraph discusses the process of deriving the equations for sine and cosine functions based on a given graph. The speaker begins by identifying the maximum and minimum points of the graph, which are at 5 and -3 respectively, leading to an amplitude of 4 and an axis at y=1. The total distance between these points is 8. The period of the function is determined by the distance between two crests or troughs, which is found to be 180 degrees. The speaker then explains how to calculate the K value, which is 2 in this case, by dividing 360 degrees by the observed period. This information is crucial for writing the equations of the sine and cosine functions that model the graph.

05:02
πŸ” Writing Sine and Cosine Functions for a Given Graph

In this paragraph, the focus shifts to writing the actual sine and cosine functions for the graph analyzed in the previous section. The speaker chooses a specific sine function on the graph that has been shifted by 45 degrees and opens downwards. The equation for this sine function is derived by incorporating the amplitude (negative due to the downward opening), the K value (2), the phase shift (-45 degrees), and the vertical shift (+1). This results in the equation y = -sin(2ΞΈ - 45) + 1. For the cosine function, the speaker identifies a function on the graph that aligns with the zero line, indicating no phase shift. The cosine function shares the same amplitude and axis as the sine function but does not have a phase shift or reflection. The resulting equation is y = cos(2ΞΈ) + 1. The speaker emphasizes that there are multiple solutions for both sine and cosine functions that could model the graph.

Mindmap
Keywords
πŸ’‘Sine Function
A sine function is a mathematical representation of a smooth, periodic oscillation. It is defined as the ratio of the length of the opposite side to the hypotenuse in a right-angled triangle, and in trigonometric functions, it represents the y-coordinate of a point on the unit circle. In the video's context, the sine function is used to model the graph of a wave with specific characteristics such as amplitude, period, and phase shift. The script mentions writing an equation for a sine function that fits the given graph, emphasizing its importance in analyzing the wave's behavior.
πŸ’‘Cosine Function
The cosine function is similar to the sine function but represents the adjacent side's ratio to the hypotenuse in a right-angled triangle or the x-coordinate on the unit circle. It is also a periodic function that oscillates between -1 and 1. The video discusses the cosine function as an alternative to the sine function for modeling the graph, highlighting that it shares the same amplitude and axis but may differ in phase shift.
πŸ’‘Amplitude
Amplitude refers to the maximum displacement of a periodic wave from its equilibrium or mean position. In the context of the video, the amplitude is determined by the distance from the axis of the curve to either the maximum (crest) or minimum (trough) of the wave. The script identifies the amplitude as four, which is half the total distance between the maximum and minimum points on the graph.
πŸ’‘Axis
The axis of a wave is the vertical line that passes through the middle of the wave, exactly halfway between the maximum and minimum points. It serves as a reference point for the wave's displacement. In the video, the axis is identified as y equals one, which is the midpoint between the crests and troughs of the graphed wave.
πŸ’‘Period
The period of a wave is the length of one complete cycle of the wave, measured from one crest (or trough) to the next. It is a key characteristic in understanding the frequency of oscillation. The script calculates the period by measuring the distance between two crests on the graph, finding it to be 180 degrees, which is crucial for determining the wave's temporal properties.
πŸ’‘Crest
A crest is the highest point of a wave, representing the peak of the oscillation. In the video, the crests are identified as points where the wave reaches its maximum value, which is five in this case. The crests are used to help determine the amplitude and the period of the wave.
πŸ’‘Trough
A trough is the lowest point of a wave, corresponding to the minimum value of the oscillation. The script mentions the troughs as being at negative values (-1, -2, -3), which, along with the crests, helps in determining the total distance that the wave travels and thus the amplitude.
πŸ’‘Phase Shift
Phase shift is the horizontal displacement of a wave from its standard position. It is often measured in degrees or radians and affects the starting point of the wave's cycle. In the video, the sine function is described as being 'pushed over by 45 degrees,' indicating a phase shift to the right, which is a critical aspect when writing the wave's equation.
πŸ’‘K Value
The K value, or angular frequency, is a factor that relates to the period of the wave. It is used in the wave's equation to determine how many cycles fit within a certain angle, typically 360 degrees. The script calculates the K value as two by dividing 360 by the observed period (180), which is essential for writing the correct equation for the wave.
πŸ’‘Graph Analysis
Graph analysis involves examining the visual representation of data to extract meaningful information. In the context of the video, graph analysis is used to identify key features of the wave, such as amplitude, period, and phase shift, by observing the graph's shape and points. This analysis is crucial for determining the appropriate mathematical equation to model the graph.
Highlights

The lesson focuses on deriving the equation for a sine or cosine function from a given graph.

The graph's crests (maximum points) are identified at y=5.

The graph's minimum points are observed at y=-3.

The total distance between the maximum and minimum points is 8, indicating the amplitude.

The axis of the curve is determined to be halfway between the crests and troughs at y=1.

The amplitude is calculated as 4, the distance from the axis to the peak or trough.

The period of the sine curve is analyzed and determined to be 180 degrees.

Exact points on the graph are revealed to gather information about the period.

The K value, based on the period, is calculated to be 2.

The process of determining the K value by dividing 360 by the observed period is explained.

The sine function is assumed for the equation derivation, with the graph analyzed for a starting point.

A sine function is identified starting at the axis and moving down and back up.

The sine function is noted to be shifted by 45 degrees to the right.

The equation of the sine function is derived with a negative amplitude due to reflection.

The cosine function is identified on the graph, with no phase shift.

The equation for the cosine function is written with a positive amplitude and no phase shift.

Multiple solutions for both sine and cosine functions are acknowledged.

Transcripts

Browse More Related Video

Precalc 5.5 Day 2 Notes

Writing Equations for Sinusoidal Functions

Writing Sine and Cosine Equations from Graphs

How to Graph the Cosine Graph with Multiple Transformations

Trigonometry - Graphing transformations of sin and cos

Writing Equations for Trig Graphs

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Sine FunctionCosine FunctionGraph AnalysisTrigonometryAmplitudePeriodPhase ShiftAxis of CurveEducational ContentMathematics LessonFunction Modeling