How to Graph the Cosine Graph with Multiple Transformations

Brian McLogan

10 Jul 201408:44

EducationalLearning

32 Likes 10 Comments

TLDRThe video script is an instructional guide on graphing the function f(x) = 3cos(x + 2π/3) - 2. It explains the process of identifying key features such as amplitude, period, phase shift, and vertical translations. The amplitude is determined as 3, the period as 2π, and the phase shift calculated to be -2π/3, leading to a downward shift of the graph by 2 units. The script then illustrates how to plot two complete periods of the transformed cosine function, emphasizing the importance of understanding the transformations and the function's behavior.

Takeaways

📈 The function to graph is f(x) = 3cos(x + 2π/3) - 2, which is a transformed cosine function.
🔄 The general form of a cosine transformation is a*cos(bx - c) + d, where 'a' is the amplitude, 'b' affects the period, 'c' is the phase shift, and 'd' is the vertical translation.
📌 To find the amplitude 'a', take the absolute value of the coefficient in front of the cosine function, which in this case is 3.
🔄 The period is calculated by dividing 2π by the coefficient 'b'. With 'b' being 1, the period is 2π.
📐 The x-scale is the period divided by 4, which for this function is π/2.
🚫 To determine the phase shift, set the expression inside the parentheses to zero and solve for 'x'. Here, the phase shift is -2π/3.
📉 The vertical translation 'd' is the constant term at the end of the function, which is -2, indicating a downward shift.
📊 Start graphing by identifying key points such as the maximum and minimum values based on the amplitude and period.
🔢 Work through the x-axis by adding the x-scale (π/2) to find subsequent points on the graph.
📈 The graph begins at -2π/3 on the x-axis and follows the pattern of the cosine function, shifted accordingly.
🎥 The final graph will show two complete periods, reflecting the changes in amplitude, phase shift, and vertical transformation.

Q & A

What is the function being graphed in the transcript?
-The function being graphed is f(x) = 3cos(x + 2π/3) - 2.
What does the 'a' value represent in the function's transformation?
-The 'a' value represents the amplitude of the function, which is the distance from the maximum to the minimum value of the graph.
How is the amplitude determined from the given function?
-The amplitude is determined by taking the absolute value of 'a', which in this case is the absolute value of 3, giving us an amplitude of 3.
What is the period of the function?
-The period of the function is calculated by dividing 2π by the value of 'b', which is 1 in this case. So, the period is 2π/1, which simplifies to 2π.
How is the phase shift determined for the given function?
-The phase shift is determined by setting the value inside the parentheses (x + 2π/3) equal to zero and solving for 'x'. This results in a phase shift of -2π/3.
What is the vertical translation of the graph?
-The vertical translation is represented by 'd' in the function. In this case, 'd' is -2, which means the graph is shifted down by 2 units.
How does the amplitude affect the graph of the function?
-The amplitude of 3 affects the graph by determining the maximum and minimum values the function reaches, which are 3 units above and 3 units below the x-axis, respectively.
What is the x scale of the graph?
-The x scale is determined by dividing the period by 4. Since the period is 2π, the x scale is 2π/4, which simplifies to π/2.
How does the phase shift of -2π/3 affect the starting point of the graph?
-The phase shift of -2π/3 affects the starting point by moving it to the left by 2π/3 units on the x-axis, which is the negative direction on the horizontal scale.
What is the process for graphing the function with the given transformations?
-The process involves starting at the phase shift (-2π/3), then moving one x scale to the right and left (π/2 units), and plotting the maximum and minimum values based on the amplitude (3 units up and down from the x-axis), while also accounting for the vertical shift (down by 2 units).
How many periods are graphed in the example provided in the transcript?
-Two complete periods of the function are graphed in the example provided in the transcript.

Outlines

00:00

📊 Understanding Trigonometric Graphs - Amplitude, Period, and Phase Shift

This paragraph introduces the process of graphing a trigonometric function, specifically f(x) = 3cos(x + 2π/3) - 2. The speaker explains the importance of understanding the impact of different numbers on the graph and identifies the need to determine the amplitude, period, x scale, phase shift, and vertical translations. The amplitude is found by taking the absolute value of 'a', the period is calculated as 2π divided by 'b', and the phase shift is determined by setting the expression inside the parentheses equal to zero. The vertical translation is identified as 'd'. The speaker then calculates these values for the given function, resulting in an amplitude of 3, a period of π, a phase shift of -2π/3, and a vertical shift down by 2 units.

05:01

📈 Plotting the Trigonometric Function - Identifying X Scale and Graphing

The speaker continues by discussing the practical steps of plotting the trigonometric function. They emphasize the importance of identifying the x scale and start by plotting a complete period to the left and right of the starting point. The amplitude's effect on the graph is explained, with the speaker noting that it represents the distance from the maximum to the minimum or the crossing of the x-axis. The speaker then calculates the x scale points, starting at -2π/3 and adding π/2 increments to find subsequent points. The graph is described as shifting down by two units, and the speaker outlines the process of plotting the maximum and minimum points to complete the graph, resulting in a clear visual representation of two periods with the given transformations.

Mindmap

Keywords

💡Graphing

Graphing is the process of visually representing data or functions on a coordinate plane. In the video, the speaker is guiding the audience through the steps to graph the function f(x) = 3cos(x + 2π/3) - 2, which involves understanding the transformations and properties of the function.

💡Amplitude

Amplitude in the context of trigonometric functions, such as cosine, refers to the maximum distance from the graph's peak or trough to the horizontal axis (x-axis). In the video, the amplitude is determined by the absolute value of 'a' in the function, which is 3, indicating the graph oscillates between 3 units above and 3 units below the x-axis.

💡Period

The period of a trigonometric function is the interval over which the function's values repeat. It is a measure of how long it takes for the function to complete one full cycle. In the video, the period is calculated by dividing 2π by the value of 'b', which is 1 in this case, resulting in a period of 2π.

💡Phase Shift

A phase shift in a trigonometric function is a horizontal translation of the graph, either to the left or right, that causes the function's cycle to start at a different point. In the video, the phase shift is determined by setting the value inside the parentheses to zero and solving for 'x', resulting in a phase shift of -2π/3.

💡Vertical Translation

Vertical translation refers to the upward or downward movement of the entire graph of a function. It is represented by the value 'd' in the function's form a times cosine of bx minus c plus d. In the video, the vertical translation is found by the value of 'd', which is -2, indicating the graph is shifted down by 2 units.

💡Transformations

Transformations are the changes made to the graph of a function that result in a new graph. These include amplitude, period, phase shift, and vertical translation. In the video, the speaker explains how each of these transformations affects the graph of the cosine function.

💡Cosine Function

The cosine function is a fundamental trigonometric function that describes periodic fluctuations or oscillations in a wave. It is used in the video to understand the basic shape and behavior of the graph of the given function f(x) = 3cos(x + 2π/3) - 2.

💡X Scale

The x scale, or x-axis scale, refers to the distance between points along the x-axis on a graph. In the video, the x scale is determined by the period and is used to identify the points where the graph reaches its maximum and minimum values.

💡Trigonometric Function

A trigonometric function is a function that relates the angles of a right-angled triangle to the ratios of its sides. In the video, the cosine function is a specific type of trigonometric function that the speaker uses to graph and analyze the given mathematical expression.

💡Coordinate Plane

A coordinate plane is a two-dimensional grid system used to represent points and shapes in a Cartesian coordinate system. In the video, the coordinate plane is the medium on which the graph of the function is drawn and analyzed.

💡Equation

An equation is a mathematical statement that asserts the equality of two expressions. In the video, the given equation f(x) = 3cos(x + 2π/3) - 2 is the starting point for the graphing process and the basis for all subsequent calculations and transformations.

Highlights

The speaker introduces a method for graphing the function f(x) = 3cos(x + 2π/3) - 2.

The process begins by identifying the components of the function to understand the transformations.

The amplitude of the function is found by taking the absolute value of 'a', which is 3 in this case.

The period is calculated by dividing 2π by 'b', resulting in a period of 2π.

The x-scale is determined by dividing the period by 4, leading to π/2.

The phase shift is calculated by setting the inside of the parentheses equal to zero, resulting in x = -2π/3.

The vertical translation is found to be -2, indicating a downward shift of the graph.

The speaker explains the impact of amplitude on the graph, which is the distance from the maximum to the minimum.

The x-scale is established by starting at -2π/3 and adding π/2 to find subsequent points.

A pattern is identified for the x-scale, adding 5π/6 for each subsequent point.

The graph is shifted down by 2 units, represented by a dashed x-axis.

The highest point of the cosine graph is determined by the amplitude of 3.

The graph's intercept, minimum, and maximum points are plotted to form one complete period.

The process is repeated to graph two complete periods with the given transformations.

The speaker emphasizes the importance of understanding the x-scale and the pattern of the cosine function.

The final graph demonstrates the combined effects of amplitude, phase shift, and vertical transformation.

Transcripts

Browse More Related Video

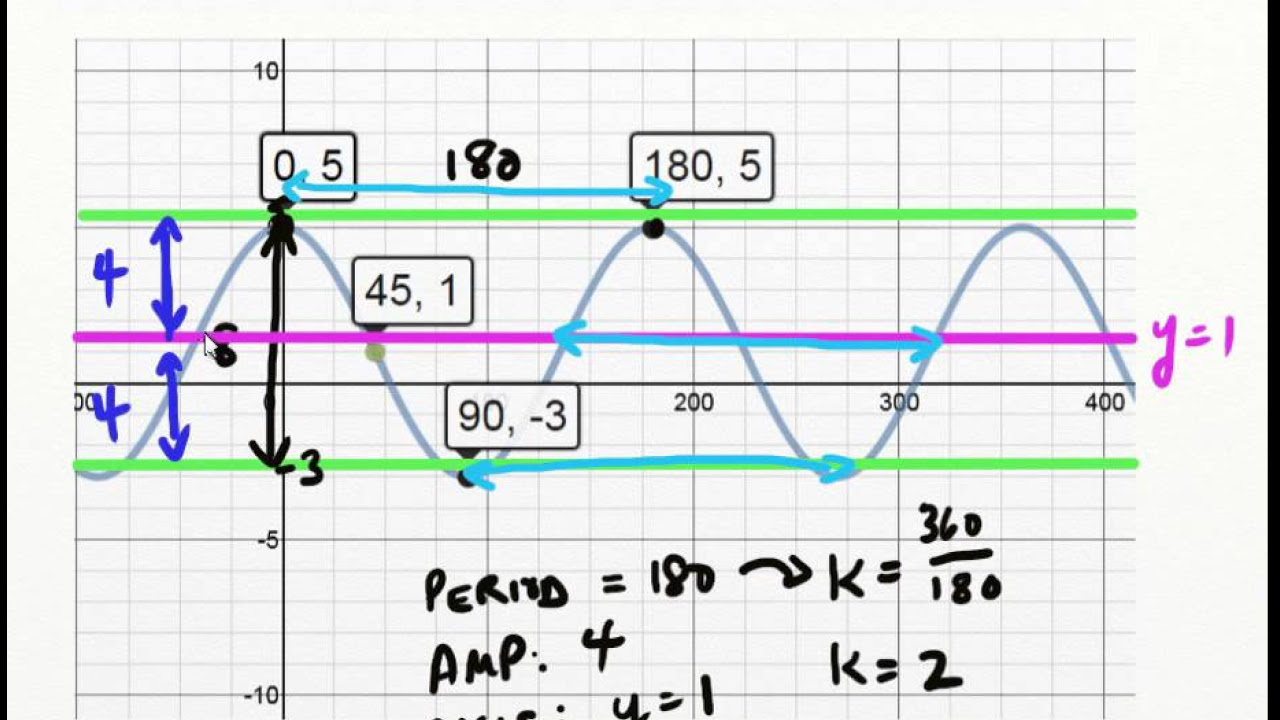
MCR3U UNIT 5 Writing Sine Cosine Equation Given Graph

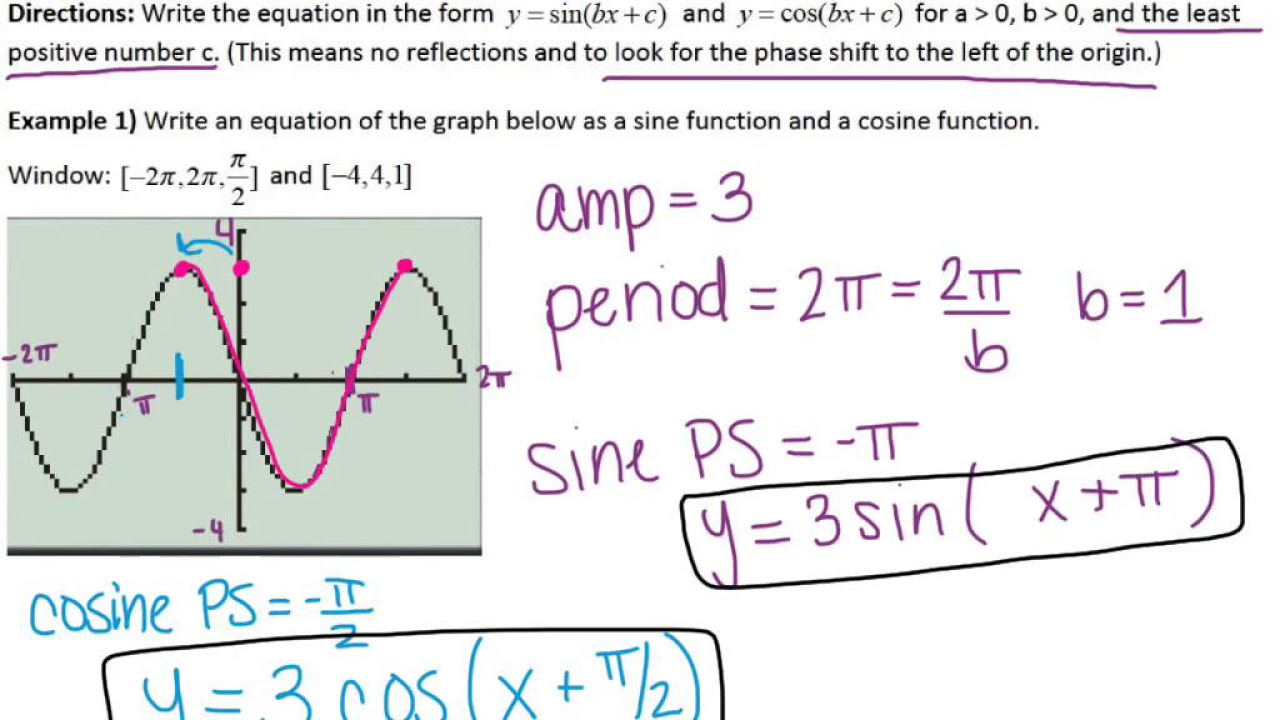
Precalc 5.5 Day 2 Notes

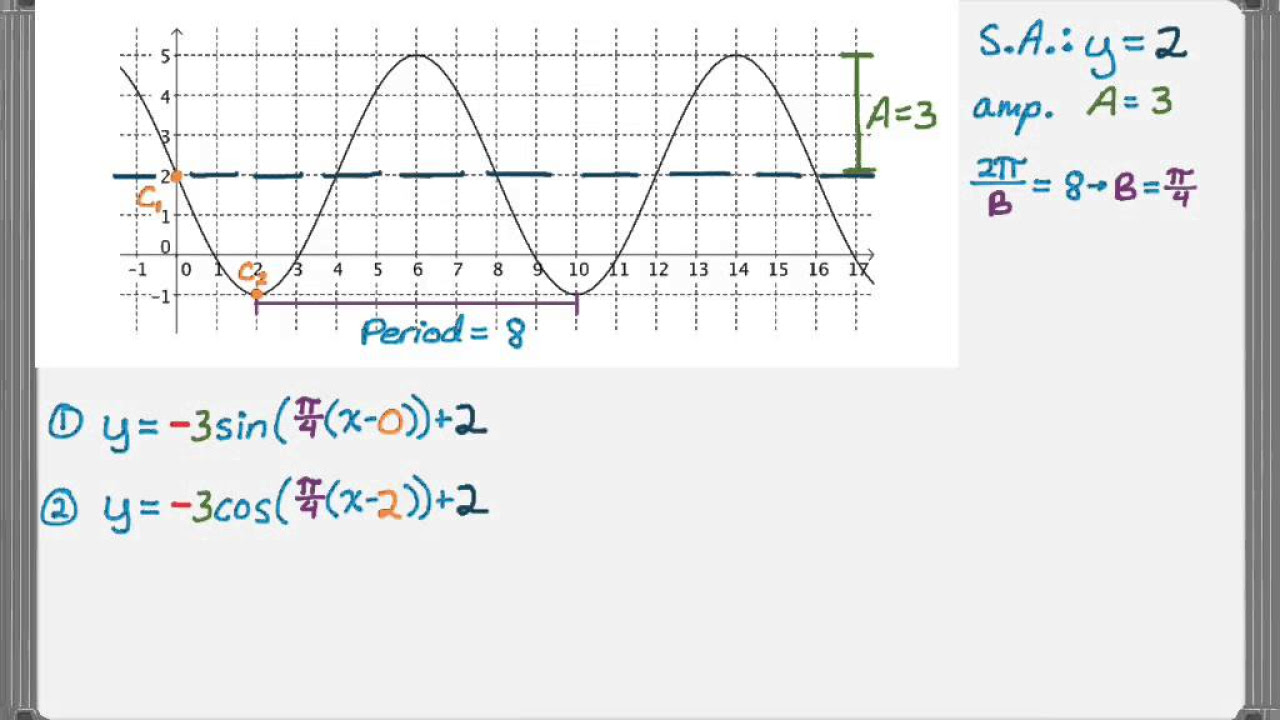
Writing Sine and Cosine Equations from Graphs

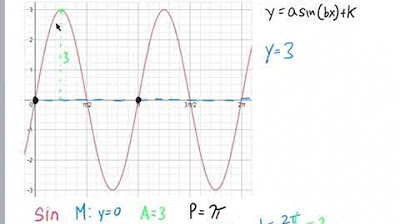
Writing Equations for Sinusoidal Functions

Graphing Sine and Cosine Trig Functions With Transformations, Phase Shifts, Period - Domain & Range

How to Graph with Transformations (Precalculus - College Algebra 15)

How to Graph the Cosine Graph with Multiple Transformations

Takeaways

Q & A

What is the function being graphed in the transcript?

What does the 'a' value represent in the function's transformation?

How is the amplitude determined from the given function?

What is the period of the function?

How is the phase shift determined for the given function?

What is the vertical translation of the graph?

How does the amplitude affect the graph of the function?

What is the x scale of the graph?

How does the phase shift of -2π/3 affect the starting point of the graph?

What is the process for graphing the function with the given transformations?

How many periods are graphed in the example provided in the transcript?