Unit Circle Definition of Trig Functions
TLDRThis trigonometry lesson introduces an extension of sine, cosine, and tangent functions beyond the basic right triangle definitions. Using the unit circle and the mnemonic 'sohcahtoa', the instructor explains how these functions can be defined for angles greater than 90 degrees or less than 0, including negative angles and those measured in radians. The sine function is shown to equal the y-coordinate, cosine as the x-coordinate, and tangent as y/x on the unit circle. Examples are given for angles like pi/2 and pi, demonstrating how these definitions handle special cases where traditional right triangle trigonometry fails.
Takeaways
- 📚 The presentation is part of a trigonometry module series, aiming to review and extend the understanding of sine, cosine, and tangent functions.
- 🔍 The mnemonic 'sohcahtoa' is introduced to help remember the definitions of sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent) in the context of a right triangle.
- 📉 The traditional right triangle definition of trigonometric functions has limitations, as it breaks down for angles approaching 90 degrees or beyond, and does not account for negative angles.
- 📐 An extension of the trigonometric function definitions is introduced using a unit circle, which allows for the functions to be defined for a broader range of angles, including those greater than 90 degrees or less than 0.
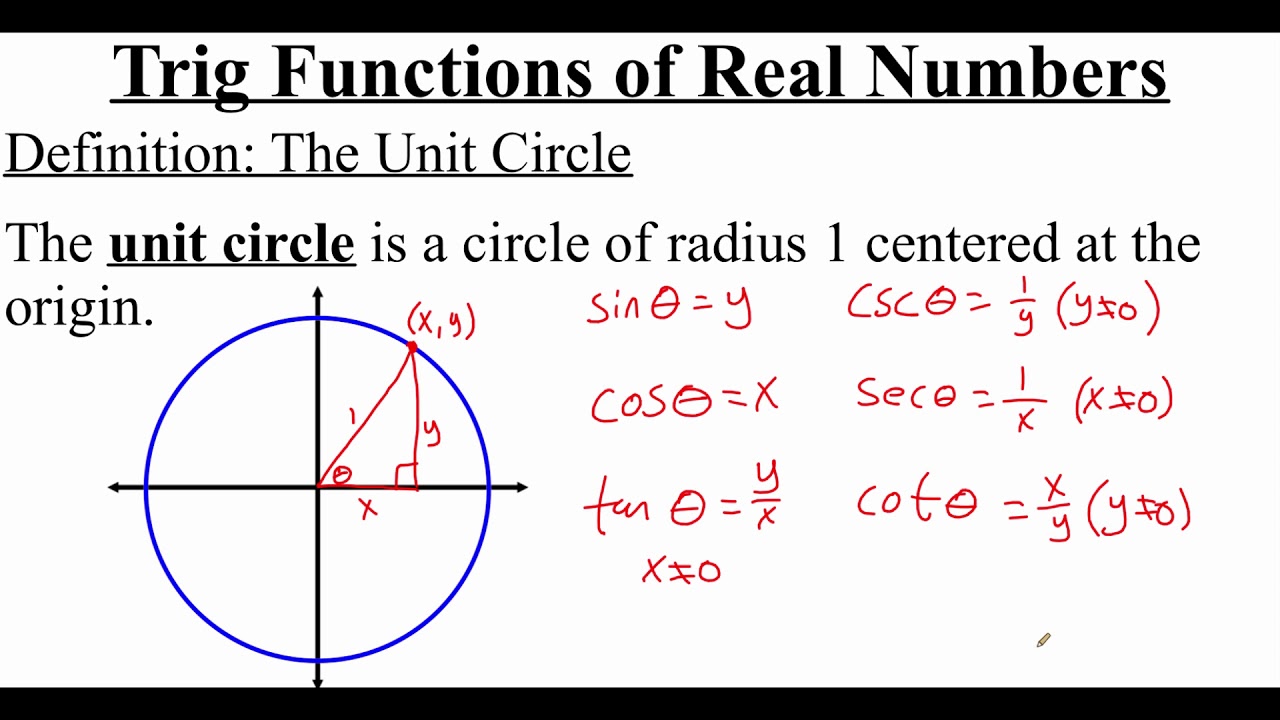
- 📈 The unit circle has a radius of 1, and the sine of an angle (theta) is defined as the y-coordinate where the radius intersects the circle, while the cosine is the x-coordinate.
- 📝 For angles where the traditional definitions do not apply, such as theta equal to 90 degrees or pi/2 radians, sine is defined as the y-coordinate and cosine as the x-coordinate on the unit circle.
- 🤔 The tangent function, defined as sine/cosine or y/x on the unit circle, can still be undefined at certain points, such as when theta equals pi/2 radians, where the x-coordinate is 0.
- 📊 The unit circle approach allows for the exploration of trigonometric functions at angles like pi radians (180 degrees), where sine is 0, cosine is -1, and tangent is 0.
- 📚 The next module will involve graphing these functions to visualize their behavior and understand their usefulness in a broader mathematical context.
- 👋 The presenter concludes by indicating that the upcoming module will further elaborate on the concepts introduced, promising a clearer understanding of the extended definitions of trigonometric functions.
Q & A
What is the purpose of the mnemonic 'sohcahtoa'?
-The mnemonic 'sohcahtoa' is used to help remember the definitions of the sine, cosine, and tangent functions in the context of a right triangle. 'Soh' stands for sine equals opposite over hypotenuse, 'cah' stands for cosine equals adjacent over hypotenuse, and 'toa' stands for tangent equals opposite over adjacent.
What limitations does the right triangle definition of trigonometric functions have?
-The right triangle definition of trigonometric functions breaks down at certain angles, such as when the angle approaches 90 degrees, or when the angle is negative, greater than 90 degrees, or even in radians like 800 degrees or 8 pi radians, because these cannot be represented within a standard right triangle.
What is a unit circle and how does it relate to the trigonometric functions?
-A unit circle is a circle with a radius of 1. It is used to extend the definition of sine, cosine, and tangent functions beyond the limitations of the right triangle. The coordinates of the point where a radius intersects the circle at a given angle can be used to define the trigonometric functions for that angle.
How is the sine of an angle defined using the unit circle?
-The sine of an angle (theta) using the unit circle is defined as the y-coordinate of the point where the radius drawn at that angle intersects the circle.
How is the cosine of an angle defined using the unit circle?
-The cosine of an angle (theta) using the unit circle is defined as the x-coordinate of the point where the radius drawn at that angle intersects the circle.
What is the significance of the angle pi over 2 radians in the context of the unit circle?
-The angle pi over 2 radians (or 90 degrees) is significant because it is the point where the sine function reaches its maximum value of 1, and the cosine function becomes 0, as the radius intersects the top of the unit circle.
What happens to the tangent function when the angle is pi over 2 radians?
-At the angle pi over 2 radians, the tangent function, which is defined as sine over cosine (or y/x), becomes undefined because the cosine (x-coordinate) is 0, and division by zero is not defined.
What happens to the sine, cosine, and tangent functions when the angle is pi radians?
-At the angle pi radians (or 180 degrees), the sine function is 0, the cosine function is -1, and the tangent function is 0, as the radius intersects the left side of the unit circle.
Why is the tangent function not defined at certain points?
-The tangent function is not defined at certain points, such as pi over 2 radians, because these points correspond to angles where the cosine (the denominator in the definition y/x) is 0, resulting in a division by zero, which is undefined.
What will be covered in the next module regarding the trigonometric functions?
-In the next module, the presenter plans to graph the trigonometric functions, showing how they behave and extend beyond the limitations of the right triangle definition, and how they can be defined for a full range of angles.
Outlines
📚 Introduction to Trigonometric Functions
This paragraph introduces the trigonometry module and reviews the definitions of sine, cosine, and tangent based on a right triangle, using the mnemonic 'sohcahtoa'. It explains that these definitions break down at certain angles, such as approaching 90 degrees or when dealing with negative or excessively large angles. To address this, the presenter introduces an extension of these definitions using a unit circle, which allows for the trigonometric functions to be defined for a broader range of angles, including those greater than 90 degrees or less than 0.
📐 Unit Circle Definition of Trigonometric Functions
The paragraph delves into the unit circle concept to extend the definitions of sine, cosine, and tangent functions. It describes how to use the unit circle, with a radius of 1, to define these functions for any angle theta. The sine of theta is defined as the y-coordinate of the point where the radius intersects the circle, while the cosine of theta is the x-coordinate. The tangent is defined as the ratio of sine to cosine (y/x). The paragraph also provides examples of how these definitions work for specific angles, such as pi/2 radians (90 degrees) and pi radians (180 degrees), demonstrating how the sine and cosine values change and how the tangent becomes undefined or zero at these points.
👋 Conclusion and Upcoming Module Preview
In the concluding paragraph, the presenter briefly mentions that the next module will involve graphing the sine, cosine, and tangent functions based on the unit circle definitions. This sets the expectation for further exploration of these trigonometric functions and their graphical representations, which will help to visualize and understand their behavior across different angles.
Mindmap
Keywords
💡Trigonometry
💡Sine
💡Cosine
💡Tangent
💡Unit Circle
💡Right Triangle
💡Mnemonic
💡Hypotenuse
💡Adjacent Side
💡Opposite Side
💡Radians
Highlights
Introduction to trigonometry modules and review of sine, cosine, and tangent definitions.
Explanation of the mnemonic 'sohcahtoa' for sine, cosine, and tangent.
Limitations of the right triangle definition for trigonometric functions as angles approach 90 degrees or become negative.
Introduction of an extension to the trigonometric function definitions using a unit circle.
Description of the unit circle and its relation to the trigonometric functions.
Derivation of sine as the y-coordinate on the unit circle for a given angle.
Derivation of cosine as the x-coordinate on the unit circle for a given angle.
Explanation of how the unit circle allows for the definition of trigonometric functions for angles greater than 90 degrees or less than 0.
Demonstration of sine and cosine values for angles approaching 90 degrees using the unit circle.
Introduction of tangent as y/x on the unit circle and its relation to sine and cosine.
Example of calculating sine, cosine, and tangent for an angle of pi/2 radians.
Discussion on the undefined tangent value at pi/2 radians and its behavior as it approaches infinity.
Calculation of sine, cosine, and tangent for an angle of pi radians (180 degrees).
Explanation of the tangent value being zero at pi radians due to the y-coordinate being zero.
Promise of graphing the trigonometric functions in the next module to show their behavior and utility.
Conclusion and sign-off for the presentation.
Transcripts
Browse More Related Video

Trigonometric Functions of Any Angle - Unit Circle, Radians, Degrees, Coterminal & Reference Angles

Trig 0.2 - Trig Functions Defined on the Unit Circle
4.3.4 Trigonometric Functions of Real Numbers
Yr 10 Trigonometry 10 - The four quadrants

30-60-90 Triangles - Special Right Triangle Trigonometry

Trigonometric Functions and the Unit Circle (Precalculus - Trigonometry 6)
5.0 / 5 (0 votes)
Thanks for rating: