4.3.4 Trigonometric Functions of Real Numbers

Justin Backeberg
3 Feb 202006:55
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, Mr. Backer introduces the concept of trigonometric functions using the unit circle, a circle with a radius of 1 centered at the origin. He explains how the unit circle relates to right triangle trigonometry, demonstrating that the sine of an angle is the y-value and the cosine is the x-value of a point on the circle. The video also covers tangent and its reciprocal functions, emphasizing the importance of avoiding division by zero. Furthermore, it explores the properties of the unit circle, including the range of sine and cosine values and the symmetry in their behavior for positive and negative angles. The Pythagorean identity, relating the sine and cosine of an angle, is introduced as a fundamental trigonometric identity.

Takeaways
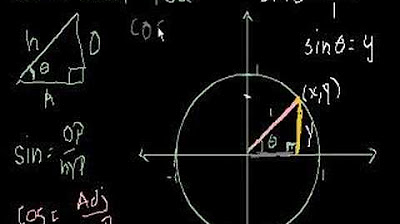
  • πŸ“ The unit circle is a circle with a radius of 1, centered at the origin, which helps connect right triangle trigonometry with trigonometric functions.
  • πŸ“ For any point on the unit circle, the horizontal distance (x) and vertical distance (y) form a right triangle with the hypotenuse being the radius (1).
  • πŸ“‰ The sine of an angle (ΞΈ) on the unit circle is equal to the y-value of the corresponding point on the circle.
  • πŸ“ˆ The cosine of an angle (ΞΈ) on the unit circle is equal to the x-value of the corresponding point on the circle.
  • 🚫 The tangent of an angle (ΞΈ) is the ratio of the opposite side (y) to the adjacent side (x), and x cannot be zero to avoid division by zero.
  • πŸ”„ The reciprocal trigonometric functions, such as cosecant (1/y), secant (1/x), and cotangent (x/y), are also defined in terms of the unit circle coordinates.
  • πŸ”’ The maximum and minimum values for cosine and sine on the unit circle are between -1 and 1, reflecting their respective x and y values.
  • πŸ” The cosine of an angle is equal to the cosine of its negative, as the x-values for both angles are the same on the unit circle.
  • πŸ”„ The sine of a negative angle is the negative of the sine of the original angle, due to the opposite y-values.
  • 🧩 The Pythagorean identity for trigonometric functions, (sin^2(ΞΈ) + cos^2(ΞΈ) = 1), is derived from the unit circle properties.
Q & A

  • What is the unit circle?

    -The unit circle is a circle with a radius of 1 that is centered at the origin. It is used to connect right triangle trigonometry with trigonometric functions.

  • How does the unit circle help in understanding trigonometric functions?

    -The unit circle allows us to relate the coordinates of a point on its circumference to the trigonometric functions of the angle formed with the positive x-axis, simplifying the relationship between the sides of a right triangle and the trigonometric ratios.

  • What is the relationship between the sine of an angle and the coordinates of a point on the unit circle?

    -The sine of an angle theta is equal to the y-coordinate of the point on the unit circle corresponding to that angle.

  • How is the cosine of an angle related to the coordinates of a point on the unit circle?

    -The cosine of an angle theta is equal to the x-coordinate of the point on the unit circle corresponding to that angle.

  • Why is it important to consider the x-coordinate when dealing with the tangent function?

    -The tangent of an angle is the ratio of the opposite side (y-coordinate) to the adjacent side (x-coordinate). It is crucial to ensure that the x-coordinate is not zero to avoid division by zero.

  • What are the reciprocal trigonometric functions and how are they related to the basic trigonometric functions?

    -The reciprocal trigonometric functions are cosecant (csc), secant (sec), and cotangent (cot). Cosecant is the reciprocal of sine, secant is the reciprocal of cosine, and cotangent is the reciprocal of tangent.

  • What is the significance of the point (1, 0) on the unit circle?

    -The point (1, 0) on the unit circle represents the maximum x-value, which corresponds to the cosine of an angle being 1. It is located on the positive x-axis.

  • How do the points (-1, 0) and (0, 1) on the unit circle relate to the trigonometric functions?

    -The point (-1, 0) represents the minimum x-value, corresponding to the cosine of an angle being -1, and the point (0, 1) represents the maximum y-value, corresponding to the sine of an angle being 1.

  • What is the trigonometric identity derived from the Pythagorean theorem in the context of the unit circle?

    -The trigonometric identity derived from the Pythagorean theorem on the unit circle is \(\sin^2(\theta) + \cos^2(\theta) = 1\), which relates the sine and cosine of an angle to the unit circle's radius.

  • How does the cosine function behave when the angle is negative?

    -The cosine function is an even function, meaning that \(\cos(\theta) = \cos(-\theta)\). This is because the x-coordinate of a point on the unit circle does not change when the angle is negated.

  • What happens to the sine function when the angle is negative?

    -The sine function is an odd function, which means that \(\sin(-\theta) = -\sin(\theta)\). This is due to the y-coordinate changing sign when the angle is negated.

Outlines
00:00
πŸ“š Introduction to Trigonometric Functions on the Unit Circle

This paragraph introduces the concept of trigonometric functions in relation to the unit circle, a circle with a radius of 1 centered at the origin. The unit circle is used to connect right triangle trigonometry with trigonometric functions. The sine of an angle is defined as the y-coordinate of a point on the circle, while the cosine is the x-coordinate. The tangent, as well as the reciprocal trigonometric functions like cosecant, secant, and cotangent, are also discussed in the context of the unit circle. The importance of avoiding division by zero when dealing with tangent, cotangent, secant, and cosecant is highlighted, ensuring the x and y values are not zero. The paragraph sets the stage for exploring the properties of the unit circle and trigonometric functions.

05:02
πŸ” Exploring Unit Circle Properties and Trigonometric Identities

The second paragraph delves into the properties of the unit circle, emphasizing its radius of 1 and how it affects the x and y coordinates of points on the circle, which correspond to the cosine and sine values, respectively. The discussion includes the points on the x-axis (1, 0) and (-1, 0), and their implications for the range of cosine values. Similarly, the points on the y-axis (0, 1) and (0, -1) define the range of sine values. The concept of angles in standard position and their trigonometric values, both positive and negative, is explored, leading to the understanding that cosine is an even function (cosine of theta equals cosine of negative theta) while sine is an odd function (sine of negative theta equals the negative of sine of theta). The paragraph concludes with the Pythagorean identity relating the sine and cosine of an angle, stating that the square of sine plus the square of cosine equals 1, which is a fundamental trigonometric identity.

Mindmap
Keywords
πŸ’‘Unit Circle
The unit circle is a circle with a radius of 1, centered at the origin of a coordinate system. It is fundamental to the video's theme as it provides a geometric context for understanding trigonometric functions. In the script, the unit circle is used to define sine and cosine in terms of the coordinates of points on its circumference, with sine being the y-coordinate and cosine the x-coordinate of a point at a given angle theta.
πŸ’‘Trigonometric Functions
Trigonometric functions are mathematical functions relating the angles of a triangle to the lengths of its sides. In the video, these functions are explored in the context of the unit circle, specifically sine, cosine, and tangent, which are defined in relation to the coordinates of points on the circle and the angle theta.
πŸ’‘Right Triangle Trig
Right triangle trigonometry is the study of the relationships between the angles and sides of right-angled triangles. The video connects this concept with the unit circle by forming a right triangle with the origin, the point on the circle at angle theta, and the x-axis, allowing for the definition of sine and cosine in terms of the triangle's sides.
πŸ’‘Sine
Sine is a trigonometric function that, in the context of the unit circle, is defined as the y-coordinate of a point on the circle corresponding to a given angle theta. It is used to describe the ratio of the opposite side to the hypotenuse in a right triangle. In the script, sine is illustrated as the vertical distance from the point on the unit circle to the x-axis.
πŸ’‘Cosine
Cosine is another trigonometric function, which for the unit circle, is the x-coordinate of a point on the circle at a given angle theta. It represents the ratio of the adjacent side to the hypotenuse in a right triangle. The video script explains that cosine remains unchanged when considering the unit circle because the hypotenuse is 1.
πŸ’‘Tangent
Tangent is a trigonometric function defined as the ratio of the opposite side to the adjacent side in a right triangle. In the video, tangent is discussed in relation to the unit circle as the ratio of the y-coordinate (sine) to the x-coordinate (cosine) of a point, with the important note that the x-coordinate (and thus the cosine) must not be zero to avoid division by zero.
πŸ’‘Reciprocal Functions
Reciprocal trigonometric functions are the inverses of the standard trigonometric functions. The video mentions cosecant (the reciprocal of sine), secant (the reciprocal of cosine), and cotangent (the reciprocal of tangent). These functions are defined in terms of the hypotenuse and the sides of a right triangle, with the video script emphasizing that the denominators (Y for cosecant and X for secant) must not be zero.
πŸ’‘Cosecant
Cosecant, or the reciprocal of sine, is a trigonometric function that relates the hypotenuse of a right triangle to its opposite side. In the script, it is defined as 1 divided by the y-coordinate of a point on the unit circle, provided that the y-coordinate is not zero.
πŸ’‘Secant
Secant is the reciprocal of cosine and is used to relate the hypotenuse of a right triangle to its adjacent side. The video script defines secant as 1 divided by the x-coordinate of a point on the unit circle, with the condition that the x-coordinate must not be zero.
πŸ’‘Cotangent
Cotangent is the reciprocal of tangent and is a trigonometric function that relates the adjacent side of a right triangle to its opposite side. The video script explains cotangent as the x-coordinate divided by the y-coordinate of a point on the unit circle, noting that the y-coordinate must not be zero to avoid division by zero.
πŸ’‘Pythagorean Theorem
The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. In the video, this theorem is applied to the unit circle to establish the identity cos(theta) squared plus sin(theta) squared equals 1, which is a fundamental trigonometric identity.
Highlights

Introduction to trigonometric functions of real numbers using the unit circle.

Explanation of the unit circle as a circle with a radius of 1 centered at the origin.

Connection between right triangle trigonometry and trigonometric functions using the unit circle.

Formation of a right triangle within the unit circle using a general X&Y point.

Definition of sine as the Y value of an ordered pair on the unit circle.

Definition of cosine as the X value of an ordered pair on the unit circle.

Tangent of theta is defined as Y over X, with the condition that X cannot be zero.

Introduction to reciprocal trigonometric functions: cosecant, secant, and cotangent.

Cosecant is the hypotenuse over the opposite side, or 1 over Y, provided Y isn't zero.

Secant is the reciprocal of cosine, or the hypotenuse over the adjacent side, or 1 over X.

Cotangent is the adjacent side over the opposite side, or X over Y, with Y not being zero.

General properties of the unit circle, including its radius length of 1.

Cosine values range between -1 and 1, corresponding to the maximum and minimum X values on the unit circle.

Sine values also range between -1 and 1, corresponding to the maximum and minimum Y values on the unit circle.

Cosine of theta equals cosine of negative theta due to the symmetry in X values.

Sine of negative theta equals the negative of sine of theta due to the opposite Y values.

Formation of a right triangle using an arbitrary angle theta on the unit circle and its properties.

Pythagorean theorem applied to the unit circle to derive the identity cos^2(theta) + sin^2(theta) = 1.

Conclusion of the video with a summary of the discussed trigonometric identities and concepts.

Transcripts

Browse More Related Video

Trig 0.2 - Trig Functions Defined on the Unit Circle

Trigonometric Functions and the Unit Circle (Precalculus - Trigonometry 6)

Trigonometry: Unit Circle

Unit Circle Definition of Trig Functions

30-60-90 Triangles - Special Right Triangle Trigonometry

Basic Trigonometric Identities: Pythagorean Identities and Cofunction Identities

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryUnit CircleRight TriangleSine FunctionCosine FunctionTangent FunctionReciprocal FunctionsPythagorean TheoremTrig IdentityEducational Content