Trigonometric Functions and the Unit Circle (Precalculus - Trigonometry 6)

Professor Leonard

9 Mar 202139:59

EducationalLearning

32 Likes 10 Comments

TLDRThis video script offers an in-depth exploration into the world of trigonometric functions, commonly referred to as 'trig functions.' The presenter aims to connect the concept of trig functions to their origins in both the unit circle and right triangle trigonometry. The script begins by explaining that trig functions relate an angle to two sides of a right triangle, with sine, cosine, and tangent being the primary functions discussed. The presenter then transitions to the unit circle—a circle with a radius of one—where every point on the circle is associated with a unique angle and arc length. The video demonstrates that on a unit circle, the arc length (t) is numerically equivalent to the central angle (in radians), a property that enables defining trig functions in terms of coordinates (x, y) on the circle. The script also covers the reciprocal trig functions: cosecant, secant, and cotangent, which are the reciprocals of sine, cosine, and tangent, respectively. The presenter concludes by emphasizing the predictability and constancy of trig functions for a given angle, regardless of the size of the triangle or circle, and hints at future discussions on quadrant angles and the application of the unit circle in trigonometry.

Takeaways

📐 Trigonometric functions relate an angle to two sides of a right triangle, creating a ratio that remains constant regardless of the triangle's size due to similar triangles.
📉 Sine, cosine, and tangent are fundamental trigonometric functions that can be visualized on a unit circle, where the radius is always one.
🔄 The unit circle allows us to define trigonometric functions based on arc length (t) and central angle (θ), which are numerically equal in radians on the unit circle.
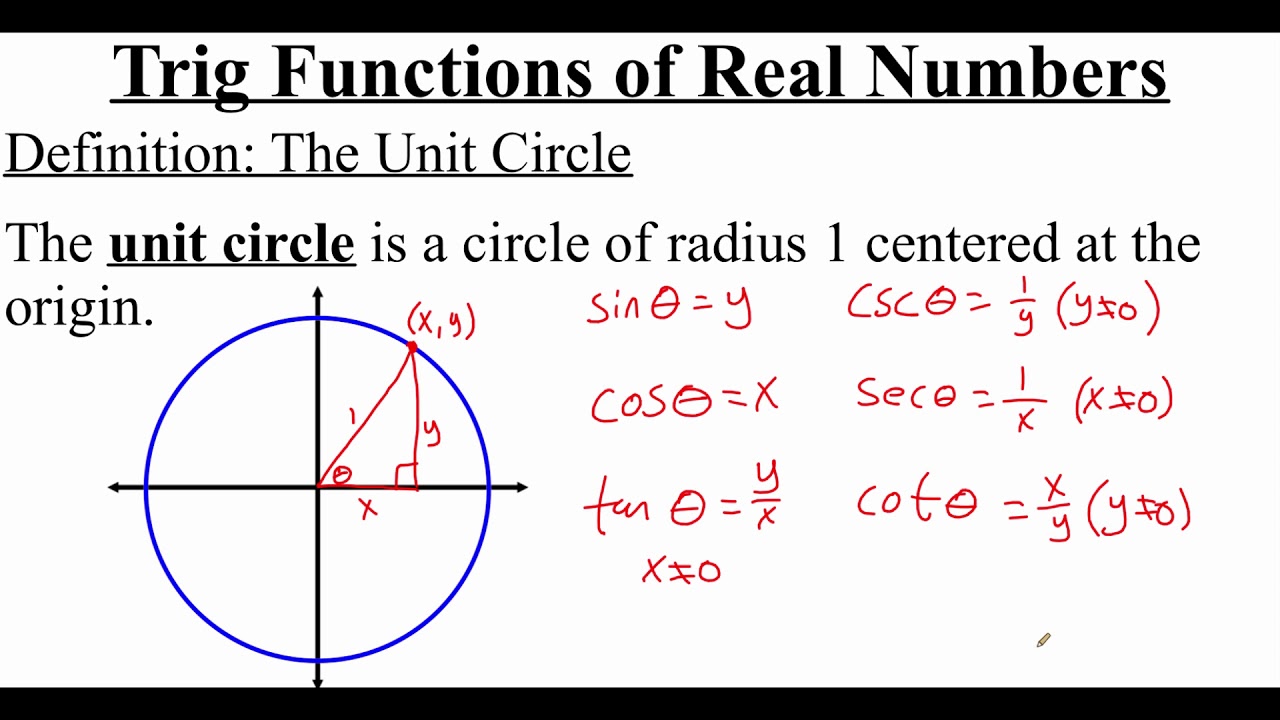
📈 Sine is defined as the y-coordinate on the unit circle, cosine as the x-coordinate, and tangent as the ratio of sine to cosine.
🔢 The range of the sine function is from -1 to 1, which corresponds to the y-coordinate on the unit circle.
🚫 Cosecant, secant, and cotangent can be undefined for certain angles because they are reciprocals of sine, cosine, and tangent, respectively.
🔁 Trigonometric functions are periodic, repeating their values in regular intervals known as their period, which is 2π for sine and cosine, and π for tangent.
🤔 The signs of the trigonometric functions depend on the quadrant of the angle being considered, which can be determined from the unit circle's x and y coordinates.
🔽 Tangent is particularly sensitive to the quadrant of the angle, as it can be undefined (approaching infinity or negative infinity) at certain points.
🔄 Reciprocal trigonometric functions like cosecant, secant, and cotangent are derived from the fundamental functions and maintain the same sign within their respective quadrants.
🧮 The Pythagorean theorem can be used to verify that a point lies on the unit circle by ensuring that the sum of the squares of its coordinates equals one.

Q & A

What are trigonometric functions commonly referred to as?
-Trigonometric functions are often called trig functions for short, due to the length of the term 'trigonometric.'
Why does the size of a right triangle not affect the trigonometric function values?
-The size of a right triangle does not affect the trigonometric function values because these values are based on the ratio of the sides, which remains constant in similar triangles.
What is the definition of a unit circle?
-A unit circle is a circle with a radius of one, where the circle intersects the x-axis at the point (1,0).
How is the arc length 't' on a unit circle related to the central angle?
-On a unit circle, the arc length 't' is numerically equal to the central angle when measured in radians, as the radius is constant at one.
What is the relationship between sine, cosine, and tangent in a right triangle?
-In a right triangle, sine relates the opposite side to the hypotenuse, cosine relates the adjacent side to the hypotenuse, and tangent is the ratio of the opposite side to the adjacent side.
Why are sine and cosine defined everywhere on the unit circle, but tangent is not?
-Sine and cosine are defined everywhere because they correspond to the y-coordinate and x-coordinate respectively, which exist for all points on the unit circle. Tangent, however, is undefined where cosine is zero, as it involves division by the x-coordinate.
What is the significance of the unit circle in defining trigonometric functions?
-The unit circle allows for a consistent definition of trigonometric functions regardless of the size of the triangle. It defines sine, cosine, and tangent directly in terms of the coordinates of a point on the circle for a given angle.
What are the reciprocal trigonometric functions?
-The reciprocal trigonometric functions are cosecant (reciprocal of sine), secant (reciprocal of cosine), and cotangent (reciprocal of tangent).
How do the signs of sine, cosine, and tangent change in different quadrants of the unit circle?
-In the first quadrant, both sine and cosine are positive, and tangent is also positive. In the second quadrant, sine is positive, but cosine is negative, making tangent negative. In the third quadrant, both sine and cosine are negative, so tangent is positive. In the fourth quadrant, sine is negative and cosine is positive, making tangent negative.
Why are trigonometric functions periodic?
-Trigonometric functions are periodic because they repeat their values in regular intervals, known as the period. For sine and cosine, the period is 2π (360 degrees), and for tangent, it is π (180 degrees), due to the nature of the unit circle and the way angles repeat after a full rotation.
How can one determine the trigonometric function values for an angle given a point on the unit circle?
-Given a point on the unit circle, one can determine the trigonometric function values by using the coordinates of the point. The sine of the angle is the y-coordinate of the point, the cosine is the x-coordinate, and the tangent is the ratio of the y-coordinate to the x-coordinate.

Outlines

00:00

📐 Introduction to Trigonometric Functions

The video introduces the topic of trigonometric functions, commonly abbreviated as 'trig functions'. The presenter aims to explore where these functions come from, showing the connection between the unit circle and right triangle trigonometry. The explanation begins with the fundamental concept that trig functions relate an angle to two sides of a right triangle. The video promises to delve into how these functions operate and represent the same angle based on side relationships, using sine, cosine, and tangent as primary examples.

05:01

🔶 Understanding Sine, Cosine, and Tangent Through Similar Triangles

The presenter discusses the concept of similar triangles to demonstrate that the ratios defined by trig functions remain constant regardless of the triangle's size. This consistency is highlighted by showing that the sine of an angle relates the opposite side to the hypotenuse, cosine relates the adjacent side to the hypotenuse, and tangent is the ratio of the opposite to the adjacent side. The video emphasizes the importance of these ratios being predictable and repeatable, and introduces the idea of using a unit circle (a circle with a radius of one) to simplify these relationships.

10:02

🌀 The Unit Circle and Central Angles

The unit circle is defined as a circle with a radius of one, and it is used to define trig functions in a different way than the right triangle approach. The video explains that for a given arc length 't', which can be positive (counterclockwise) or negative (clockwise), there is a unique point on the circle and a unique central angle. The arc length, in the case of a unit circle, is numerically equal to the central angle when measured in radians. This relationship allows for the definition of trig functions based on the arc length or central angle, leading to a clear connection between these functions and points on the unit circle.

15:04

🔄 Trigonometric Functions and Their Reciprocal Relationships

The video outlines how trigonometric functions can be defined using the unit circle and how they relate to right triangles. It emphasizes the constancy of trig function values for a given angle, regardless of the triangle's size. The presenter introduces the abbreviations for the trig functions and explains the reciprocal relationships between them: sine and cosecant, cosine and secant, tangent and cotangent. The video also discusses how these functions can be defined by the coordinates of a point on the unit circle, with sine corresponding to the y-coordinate, cosine to the x-coordinate, and tangent to the ratio of y over x.

20:05

📈 Trigonometric Functions and Their Periodicity

The presenter explores the values of trig functions at quadrant angles (0, 90, 180, 270, 360 degrees) and explains that sine and cosine are defined everywhere, while tangent, cotangent, secant, and cosecant can be undefined at certain angles. The video illustrates the periodic nature of trig functions, noting that they repeat every full rotation (2π or 360 degrees). It also touches on the concept of coterminal angles and how they share the same point on the unit circle, leading to the same trig function values.

25:06

🤔 Applying the Unit Circle to Trigonometric Functions

The video concludes with a practical application of the unit circle to determine the values of trig functions for a given point in quadrant two. It demonstrates how to find sine, cosine, and tangent for a specific angle based on the point's coordinates on the unit circle. The presenter also calculates the reciprocal functions, noting the need to rationalize the denominator when dealing with square roots. The video emphasizes the utility of the unit circle in finding trig function values and sets the stage for a more in-depth exploration in the next video.

Mindmap

Keywords

💡Trigonometric functions

Trigonometric functions, often abbreviated as trig functions, are mathematical functions that relate an angle to the ratios of two sides of a right triangle. In the video, they are used to explore the relationships between angles and the sides of triangles, as well as their representation on the unit circle. The script discusses how these functions are fundamental to understanding the geometry of triangles and the coordinate relationships on a unit circle.

💡Unit circle

A unit circle is a circle with a radius of one and is centered at the origin of a coordinate system. It plays a crucial role in the video as it provides a geometric interpretation of trigonometric functions. The script explains how angles can be measured by the arc length they create on the unit circle, and how this relates to the x and y coordinates of the points on the circle, which correspond to the values of cosine and sine, respectively.

💡Right triangle

A right triangle is a triangle that has one angle measuring 90 degrees. The video uses the concept of right triangles to introduce trigonometric functions, explaining how the sine, cosine, and tangent of an angle in a right triangle relate to the ratios of the triangle's sides. The script emphasizes that the size of the triangle does not affect the trigonometric function values due to the concept of similar triangles.

💡Sine, Cosine, and Tangent

Sine (sin), cosine (cos), and tangent (tan) are the three primary trigonometric functions. The video defines these as the ratios of the sides in a right triangle, with sine being the ratio of the opposite side to the hypotenuse, cosine the ratio of the adjacent side to the hypotenuse, and tangent the ratio of the opposite side to the adjacent side. These functions are also related to the coordinates of points on the unit circle, as explained in the script.

💡Arc length

Arc length is the distance along the path of a segment of a curve. In the context of the unit circle, the arc length is used to define the position of points on the circle and is directly related to the central angle, which is the angle formed at the center of the circle by two radii that connect the center to the endpoints of an arc. The script explains that on a unit circle, the arc length is numerically equal to the central angle when measured in radians.

💡Central angle

A central angle is an angle whose vertex is at the center of a circle and whose sides are radii of the circle that connect to the endpoints of an arc. The video uses the central angle to establish a relationship with the arc length on the unit circle. The script demonstrates that each unique arc length on the unit circle corresponds to a unique central angle, which in turn corresponds to a specific point on the circle.

💡Reciprocal functions

Reciprocal functions in trigonometry are the inverses of the primary trigonometric functions. The cosecant (csc), secant (sec), and cotangent (cot) are the reciprocals of sine, cosine, and tangent, respectively. The video explains that these functions are defined based on the primary trig functions and are used to find the angles when the side lengths of a right triangle are known. The script illustrates how these reciprocals are derived and their relationship to the unit circle.

💡Similar triangles

Similar triangles are triangles that have the same shape but different sizes. The video uses the concept of similar triangles to explain the invariance of trigonometric function values regardless of the size of the triangle. The script points out that the ratios of the sides, and thus the trigonometric functions, remain constant for triangles that are similar, which is why the trigonometric functions can be used predictably across different sizes of triangles.

💡Quadrant angles

Quadrant angles refer to the angles that are aligned with the axes in a coordinate system, typically 0, 90, 180, 270, and 360 degrees. The video discusses how these angles are used to find the coordinates of points on the unit circle and to determine the values of trigonometric functions at these specific angles. The script uses quadrant angles to demonstrate the periodic nature of trigonometric functions and their values in different quadrants.

💡Periodicity

Periodicity in trigonometric functions refers to the repeating pattern of these functions at regular intervals. The video highlights that sine and cosine functions repeat every full rotation (360 degrees or 2π radians), while the tangent function repeats every 180 degrees (π radians). The script explains this concept by showing how the values of the trigonometric functions repeat for angles that are coterminal, which are angles that differ by a full rotation.

💡Pythagorean theorem

The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This theorem is used in the video to verify that a point lies on the unit circle by showing that the sum of the squares of its coordinates equals one. The script demonstrates its application in the context of finding trigonometric function values for points on the unit circle.

Highlights

Introduction to trigonometric functions, often abbreviated as trig functions, and their importance in mathematics.

Explaining the two different approaches to understanding trig functions: through the unit circle and in relation to a right triangle.

The concept that trigonometric functions relate an angle to two sides of a right triangle, creating a ratio that remains constant regardless of the triangle's size.

Defining sine, cosine, and tangent in terms of the sides of a right triangle, with sine as opposite over hypotenuse, cosine as adjacent over hypotenuse, and tangent as opposite over adjacent.

The realization that tangent can be expressed as sine divided by cosine, showcasing the interconnectedness of these functions.

The introduction of the unit circle, a circle with a radius of one, as a means to define trig functions in a different but related way to right triangles.

Understanding that arc length (t) on a unit circle corresponds to a unique point and a unique central angle, which is key to defining trig functions.

The equivalence of arc length and central angle measured in radians on a unit circle, simplifying the definitions of trigonometric functions.

Defining sine and cosine in terms of the coordinates of a point on the unit circle, with sine being equal to the y-coordinate and cosine equal to the x-coordinate.

Tangent is defined as the ratio of the y-coordinate to the x-coordinate on the unit circle, relating back to the right triangle definition.

Exploring reciprocal trigonometric functions such as cosecant, secant, and cotangent, which are the reciprocals of sine, cosine, and tangent respectively.

The significance of the unit circle in defining trigonometric functions for all angles, not just those in a right triangle.

The periodic nature of trig functions, repeating every full rotation (2π or 360 degrees), which is a fundamental concept in trigonometry.

The use of the unit circle to find the values of sine, cosine, and tangent for specific quadrant angles like 0, π/2, π, 3π/2, and 2π.

The behavior of trig functions in different quadrants, with sine and cosine being positive in the first and fourth quadrants, and tangent being negative in the second and third quadrants.

The concept of coterminal angles and how they share the same point on the unit circle, leading to the same trig function values.

The practical application of the unit circle in determining the values of trig functions for any given angle, simplifying complex trigonometric calculations.

The Pythagorean theorem's role in verifying that a point lies on the unit circle, by ensuring the sum of the squares of its coordinates equals one.

The importance of understanding the signs of trig function values in different quadrants, which is crucial for solving problems involving quadrant-specific angles.

Transcripts

Browse More Related Video

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

4.3.4 Trigonometric Functions of Real Numbers

Trig 0.2 - Trig Functions Defined on the Unit Circle

Trigonometric Functions of Any Angle - Unit Circle, Radians, Degrees, Coterminal & Reference Angles

How to Use the Unit Circle in Trigonometry (Precalculus - Trigonometry 7)

Reciprocal Identities in Trigonometry (Precalculus - Trigonometry 9)

Related Tags

Trigonometry Unit Circle Right Triangle Sine Cosine Tangent Cosecant Secant Cotangent Arc Length Central Angle Math Education Geometry Trig Functions Sine Cosine Tangent Similar Triangles