How To Use The Quadratic Formula To Solve Equations
TLDRThis educational video script teaches the use of the quadratic formula to solve quadratic equations in the form of y = ax^2 + bx + c. It walks through various examples, demonstrating how to identify coefficients, calculate discriminants, and find real or complex solutions. The script also addresses equations with fractional or decimal coefficients, showing how to simplify them before applying the quadratic formula. The goal is to provide a clear understanding of solving quadratic equations with different types of coefficients.
Takeaways
- 📚 The video explains the quadratic formula, which is used to solve quadratic equations of the form \( y = ax^2 + bx + c \).
- 🔍 The coefficients in the quadratic equation are identified as \( a \) (in front of \( x^2 \)), \( b \) (in front of \( x \)), and \( c \) (the constant term).
- 📐 The quadratic formula is given by \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \), where the discriminant \( b^2 - 4ac \) determines the nature of the solutions.
- 📉 If the discriminant is negative, the quadratic equation has no real solutions and instead has two complex solutions.
- 📈 If the discriminant is zero, there is exactly one real solution (the roots are the same).
- 📊 If the discriminant is positive, there are two distinct real solutions.
- 📝 The script demonstrates the process of solving quadratic equations using the quadratic formula with several examples.
- 🔢 The video provides a step-by-step guide on how to identify the values of \( a \), \( b \), and \( c \) from a given quadratic equation.
- 🌐 The script covers examples with both integer and fractional coefficients, showing how to clear fractions by multiplying through by the least common multiple.
- 🔄 It also addresses equations with decimal coefficients, suggesting multiplying by a factor to convert decimals to whole numbers for easier calculation.
- 🤔 The video encourages viewers to pause and attempt solving the equations themselves before revealing the answers.
- 🎓 The final takeaway is a reminder to check for the possibility of simplifying square roots in the solutions obtained from the quadratic formula.
Q & A
What is the standard form of a quadratic equation?
-The standard form of a quadratic equation is y = ax^2 + bx + c, where a, b, and c are constants, with 'a' not equal to zero.
What is the quadratic formula used for?
-The quadratic formula is used to find the solutions for x in a quadratic equation of the form ax^2 + bx + c = 0.
What are the values of 'a', 'b', and 'c' in the quadratic formula?
-In the quadratic formula, x = (-b ± √(b^2 - 4ac)) / (2a), 'a' is the coefficient of x^2, 'b' is the coefficient of x, and 'c' is the constant term.
How do you determine the discriminant in the quadratic formula?
-The discriminant in the quadratic formula is the expression under the square root, b^2 - 4ac, which determines the nature of the roots of the quadratic equation.
What does a negative discriminant indicate about the solutions of a quadratic equation?
-A negative discriminant indicates that the quadratic equation has no real solutions, but rather two complex or imaginary solutions.
How can you solve a quadratic equation that is not in standard form?
-To solve a quadratic equation not in standard form, you should first rearrange it into the standard form ax^2 + bx + c = 0, and then apply the quadratic formula.
What is the significance of the term 'real solutions' in the context of quadratic equations?
-Real solutions refer to the x-values that can be expressed as real numbers. If the discriminant is positive, there are two real solutions; if it's zero, there is one real solution (a repeated root).
How do you handle a quadratic equation with fractional coefficients?
-To handle a quadratic equation with fractional coefficients, you can multiply both sides of the equation by the least common multiple of the denominators to clear the fractions before applying the quadratic formula.
What should you do if the quadratic formula results in a radical that cannot be simplified?
-If the radical in the quadratic formula cannot be simplified, you should leave the answer in its current form, possibly converting it to a decimal if necessary, for practical use.
Can you provide an example of how to multiply a quadratic equation by a constant to clear decimals?
-Yes, for a quadratic equation with decimal coefficients, you can multiply each term by a power of 10 that corresponds to the number of decimal places. For example, multiplying each term by 100 for coefficients with two decimal places will eliminate the decimals.
What is the purpose of the imaginary unit 'i' in solving quadratic equations with a negative discriminant?
-The imaginary unit 'i' is used to represent the square root of negative one. It is used in the solutions of quadratic equations when the discriminant is negative, indicating that the solutions are complex numbers in the form of a + bi.
Outlines
📚 Introduction to Quadratic Formula
This paragraph introduces the quadratic formula, a fundamental tool in algebra for solving quadratic equations of the form y = ax^2 + bx + c. It explains the standard form of a quadratic equation and demonstrates the formula's application using the example x^2 + 6x + 8 = 0. The process involves identifying coefficients a, b, and c, and then substituting them into the formula to find the values of x. The explanation also includes an alternative example, x^2 - 5x - 7 = 0, encouraging viewers to solve it on their own.
🔍 Solving Quadratics with the Quadratic Formula
This section delves deeper into the application of the quadratic formula, showcasing how to handle different forms of quadratic equations. It begins with solving 8x - x^2 - 15 = 0, which is not in standard form, by rearranging it and multiplying through by -1 to make the x^2 term positive. The paragraph also discusses the concept of the discriminant (b^2 - 4ac), explaining its implications for the nature of the solutions: real, complex, or a single solution. An example with a negative discriminant, x^2 + 5x + 8, is used to illustrate how to find complex solutions.
🔢 Handling Quadratics with Fractional and Decimal Coefficients
The paragraph addresses the challenge of solving quadratic equations with fractional or decimal coefficients. It suggests clearing fractions by finding the least common multiple, in this case, 12, and multiplying through to eliminate them. The example 2/3x^2 - 5/2x + 1/4 = 0 is used to demonstrate this process. For equations with decimal coefficients, such as .1x^2 - .15x - .24, the strategy involves multiplying by 100 to convert the decimals to whole numbers, simplifying the application of the quadratic formula. Each method is illustrated with step-by-step calculations.
📉 Understanding the Discriminant's Role in Solution Types
This part of the script focuses on the discriminant's role in determining the number and type of solutions a quadratic equation will have. It explains that a negative discriminant results in no real solutions, a zero discriminant indicates one real solution, and a positive discriminant means two real solutions. The explanation is supported by examples, including one with a positive discriminant, 3x^2 - 5x + 7, which leads to complex solutions due to the large positive discriminant.
🎓 Conclusion and Final Examples
The final paragraph wraps up the video with a summary of the key points covered and presents additional examples to reinforce learning. It includes solving a quadratic equation with a large discriminant, 5x^2 + 7x - 9, resulting in an irrational solution. The video concludes with a reminder to check for possible simplifications of the square root in the solutions and thanks viewers for watching, wishing them a great day.
Mindmap
Keywords
💡Quadratic Formula
💡Quadratic Equation
💡Discriminant
💡Imaginary Numbers
💡Standard Form
💡Coefficients
💡Square Root
💡Complex Solutions
💡Least Common Multiple (LCM)
💡Decimal Coefficients
💡Simplifying Radicals
Highlights
Introduction to the quadratic formula and its application in solving quadratic equations.
Explanation of the standard form of a quadratic equation: y = ax^2 + bx + c.
Step-by-step demonstration of using the quadratic formula to solve an example equation x^2 + 6x + 8 = 0.
Calculation of the discriminant (b^2 - 4ac) to determine the nature of the solutions.
Finding square roots and solving for x, resulting in two real solutions for the first example.
Second example with the equation x^2 - 5x - 7 = 0, leading to two real solutions.
Handling non-standard form equations by rearranging and multiplying to fit the quadratic formula.
Solving the rearranged equation 8x - x^2 - 15 = 0, resulting in two real solutions.
Dealing with complex solutions when the discriminant is negative, as shown in the equation x^2 + 5x + 8 = 0.
Explanation of the discriminant's role in determining the number of real solutions (0, 1, or 2).
Example with the equation 3x^2 - 5x + 7, leading to complex solutions.
Demonstration of solving a quadratic equation with fractional coefficients by clearing fractions.
Solving a quadratic equation with decimal coefficients by multiplying to eliminate decimals.
Final example with the equation 5x^2 + 7x - 9, resulting in two real solutions.
Advice on simplifying radicals and checking for divisibility to simplify solutions.
Conclusion summarizing the process and thanking viewers for watching.
Transcripts
Browse More Related Video

How to program the quadratic formula into a TI-84 or TI-84 Plus CE

How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course
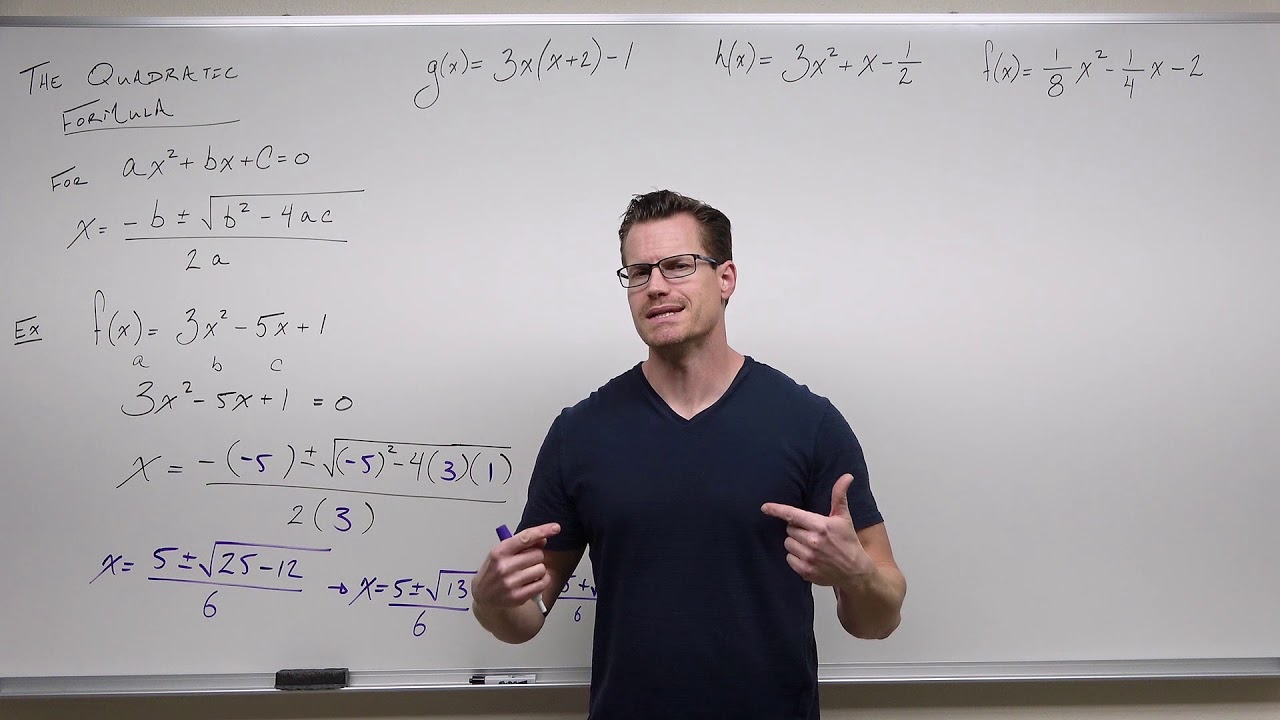
Using the Quadratic Formula (Precalculus - College Algebra 21)
How to Factor any Quadratic Equation Easily - Trick for factorising
Completing The Square Method and Solving Quadratic Equations - Algebra 2
Solving Polynomial Equations Using Goal Seek In Excel
5.0 / 5 (0 votes)
Thanks for rating: