Powell’s Pi Paradox: the genius 14th century Indian solution
TLDRThe Mathologer explores Powell's Pi Paradox, a surprising phenomenon where the series expansion of π converges incredibly slowly yet shares coincidental digit matches with π. The video delves into ancient Indian mathematics, revealing how Madhava's advanced calculus insights led to correction terms that significantly improved π approximations. It explains how these correction terms can be translated into new series for π and discusses the significance of these findings in the broader context of mathematical history.
Takeaways
- 🔍 Powell's Pi Paradox is a mathematical curiosity where an infinite series of odd denominators converges to Pi, yet the first few million terms yield only a few correct digits of Pi.
- 📚 The script introduces ancient Indian mathematics, revealing that Madhava of Sangamagrama discovered the series for Pi centuries before Leibniz and Gregory, highlighting a historical oversight.
- 📉 The convergence of the series to calculate Pi is extremely slow, which is surprising given the simplicity of the formula and the ubiquity of Pi in mathematics.
- 🤔 The paradox deepens with the observation that certain digits of Pi match the series sum for an unexpectedly long sequence, challenging intuition about random convergence.
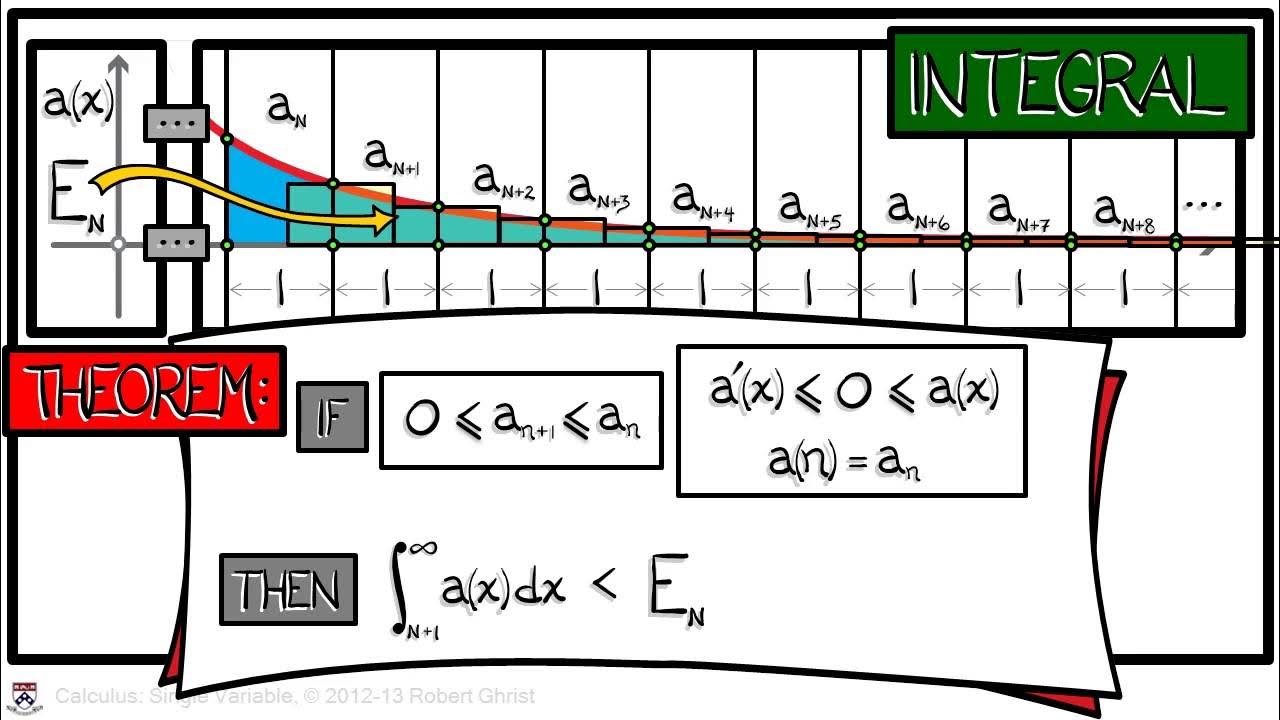
- 📝 The script explains that the series can be manipulated to improve the approximation of Pi by adding or subtracting half of the final term, a technique used by Madhava.
- 🧩 Madhava discovered patterns in the differences between the series' partial sums and the value of Pi, which led to a method of refining the approximation of Pi.
- 📈 The script describes a correction term that, when applied, significantly improves the approximation of Pi derived from the series, increasing the number of correct digits.
- 🔢 Madhava's correction terms are based on patterns observed in the fractions resulting from the difference between the series' partial sums and the approximation 355/113 of Pi.
- 📜 The ancient Indian mathematicians expressed their formulas in verse, which is a unique way of recording mathematical knowledge compared to modern mathematical notation.
- 🌐 The script connects the historical and cultural context of Indian mathematics to the broader narrative of mathematical discovery and the development of calculus.
- 🔑 The explanation of Powell's Pi Paradox relies on understanding the patterns and correction terms discovered by Madhava, which provide insight into the nature of the series' convergence.
Q & A
What is Powell's Pi Paradox?
-Powell's Pi Paradox refers to the surprising and paradoxical behavior observed when comparing the digits of the sum of the series derived from odd numbers to the actual value of Pi. Despite the series converging very slowly, there are stretches where the digits of the series and Pi match perfectly for a while before diverging again.
Who discovered the series for Pi that is central to Powell's Pi Paradox?
-The series for Pi, which is central to the paradox, was originally discovered by the Indian astronomer and mathematician Madhava of Sangamagrama, predating Leibniz and Gregory by at least 200 years.
How did Madhava and his disciples derive the series for Pi?
-Madhava and his disciples derived the series for Pi using advanced mathematical techniques that are similar to calculus, including derivatives and integrals, which they discovered centuries before Newton and Leibniz are credited with inventing calculus.
What is the significance of the correction terms in the context of the series for Pi?
-The correction terms are significant as they allow for much better approximations of Pi by adjusting the partial sums of the series in a smart way. These correction terms were discovered by Madhava and his disciples and were used to speed up the slow convergence of the series.
What is the pattern observed in the differences between the partial sums of the series and the value of Pi?
-The pattern observed in the differences is that the bottom numbers (denominators) are approximately equal to the top numbers (numerators) plus a bit, and this 'bit' increases progressively, forming a sequence of fractions where the denominator is a multiple of the numerator plus a small constant.
How did Madhava's correction terms lead to new formulas for Pi?
-Madhava's correction terms, when applied to the series, resulted in new sequences of numbers. The series corresponding to these new sequences were found to be new formulas for Pi, featuring very quickly converging series, which were expressed in a concise and beautiful form.
What is the role of the fraction 355/113 in the explanation of Powell's Pi Paradox?
-The fraction 355/113 is an approximation of Pi that was known to the Indian mathematicians. It was used to compare the partial sums of the series to identify patterns in the differences, which helped in discovering the correction terms that improved the approximation of Pi.
Why was the discovery of the series for Pi and its properties not recognized in the Western world until recently?
-The original records of Madhava's work were lost over time, and it wasn't until later commentaries by members of his school that his mathematical discoveries were recognized. The Western world's acknowledgment of these achievements came even later, reflecting a historical oversight.
How did the ancient Indian mathematicians express their mathematical formulas?
-In the ancient Indian palm leaf manuscripts, the mathematical formulas, including those for Pi, were expressed in verse, indicating a unique cultural approach to recording mathematical knowledge.
What are some of the insights that can be gained from the video script about the historical development of mathematics?
-The script highlights the advanced mathematical knowledge of ancient Indian mathematicians, their use of calculus before it was formally recognized in the Western world, and the cultural significance of expressing mathematical formulas in verse. It also underscores the importance of historical records and the challenges of recognizing and acknowledging contributions from different cultures.
Outlines
🔍 Powell's Pi Paradox Introduction
This paragraph introduces the topic of Powell's Pi Paradox, a mathematical curiosity involving the approximation of Pi using an infinite series of odd numbers. The presenter mentions the use of ancient Indian mathematical techniques to unravel this paradox. The script also highlights the Leibniz formula for Pi, which is an infinite series, and the presenter's intention to explore its convergence properties by summing the first million terms, revealing an unexpected alignment with the actual digits of Pi, despite the slow convergence rate.
📚 Ancient Indian Mathematics and Pi Approximations
This section delves into the history of the Pi formula, revealing that it was first discovered by the Indian mathematician Madhava, predating Leibniz and Gregory. The paragraph discusses the advanced mathematical techniques used by Madhava, which are akin to calculus, to derive the formula for Pi. It also mentions the power series expansion of the inverse tangent function and how Madhava's methods were ahead of his time, including his knowledge of series for sine and cosine. The presenter then explores the slow convergence of the series and Madhava's strategies to improve the approximation of Pi, introducing the concept of adjusting the last term added to the series for better accuracy.
🔢 Pattern Recognition in Pi Approximations
The focus of this paragraph is on identifying patterns in the differences between the partial sums of the series and the value of Pi. The presenter suggests using known approximations of Pi, such as 355/113, to detect these patterns. The script describes a methodical approach to finding a pattern in the fractions resulting from these differences, revealing a consistent relationship between the numerators and denominators. This leads to the discovery of a pattern where the denominator is approximately a multiple of the numerator, which is then used to refine the approximation of Pi, significantly improving the accuracy of the series.
🌐 Explaining Powell's Pi Paradox with Ancient Insights
This paragraph aims to explain Powell's Pi Paradox using the ancient Indian mathematical patterns discovered by Madhava. The presenter discusses the first correction term and how it accounts for the initial discrepancy between the partial sum and Pi. The explanation extends to the structure of the correction terms, which have a '0, 9' pattern that corresponds to regions of coincidence between the series sum and Pi. The presenter also touches upon the limitations of Madhava's third correction term and hints at the existence of a fourth term that could explain the remaining coincidences not accounted for by the third term.
📜 Legacy and Manuscripts of Madhava
The final paragraph pays tribute to the medieval Indian mathematicians, particularly Madhava, for their significant contributions to calculus and mathematical analysis. It discusses the loss of original records and the reliance on later commentaries for understanding Madhava's work. The presenter expresses admiration for the proofs provided by Madhava and his school, which were considered complete even by modern standards. The paragraph concludes with a mention of Madhava's additional Pi formulas derived from his correction terms, which were expressed in verse in the old Indian manuscripts, highlighting the beauty and ingenuity of these ancient mathematical expressions.
Mindmap
Keywords
💡Powell's Pi Paradox
💡Medieval Mathematics
💡Alternating Series
💡Convergence
💡Madhava of Sangamagrama
💡Leibniz Formula
💡Calculus
💡Correction Terms
💡Infinite Series
💡Approximation
💡Pi (π)
Highlights
Introduction to Powell’s Pi Paradox, a mathematical curiosity involving the digits of Pi.
Use of medieval Indian mathematics to resolve the paradox, highlighting the contributions of Indian mathematicians.
Pi formula derived from odd numbers, showcasing a series that converges slowly but intriguingly.
Demonstration of the slow convergence of the series by summing the first million terms.
Unexpected coincidence of digits between Pi and the series sum, sparking the paradox.
Discovery of the Pi paradox by Martin Powell in 1983, despite extensive prior knowledge of Pi.
Recognition of the ancient Indian mathematician Madhava as the precursor to Leibniz and Gregory in discovering the Pi formula.
Madhava's advanced knowledge of calculus, predating Leibniz and Newton by centuries.
Madhava's discovery of hidden patterns in the Pi series that improved its convergence rate.
Explanation of the alternating series pattern in the Pi formula and its implications.
Madhava's innovative method of adjusting the series sum for better approximations of Pi.
Identification of a pattern in the differences between partial sums and the value of Pi.
Use of the approximation 355/113 to uncover patterns in the series differences.
Madhava's correction terms that significantly improved the accuracy of Pi approximations.
Explanation of how to translate correction terms into new series formulas for Pi.
Madhava's missed opportunity to discover further correction terms due to using an approximation of Pi.
The historical significance and recognition of Madhava's mathematical achievements.
Madhava's unique presentation of mathematical formulas in verse within palm leaf manuscripts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: