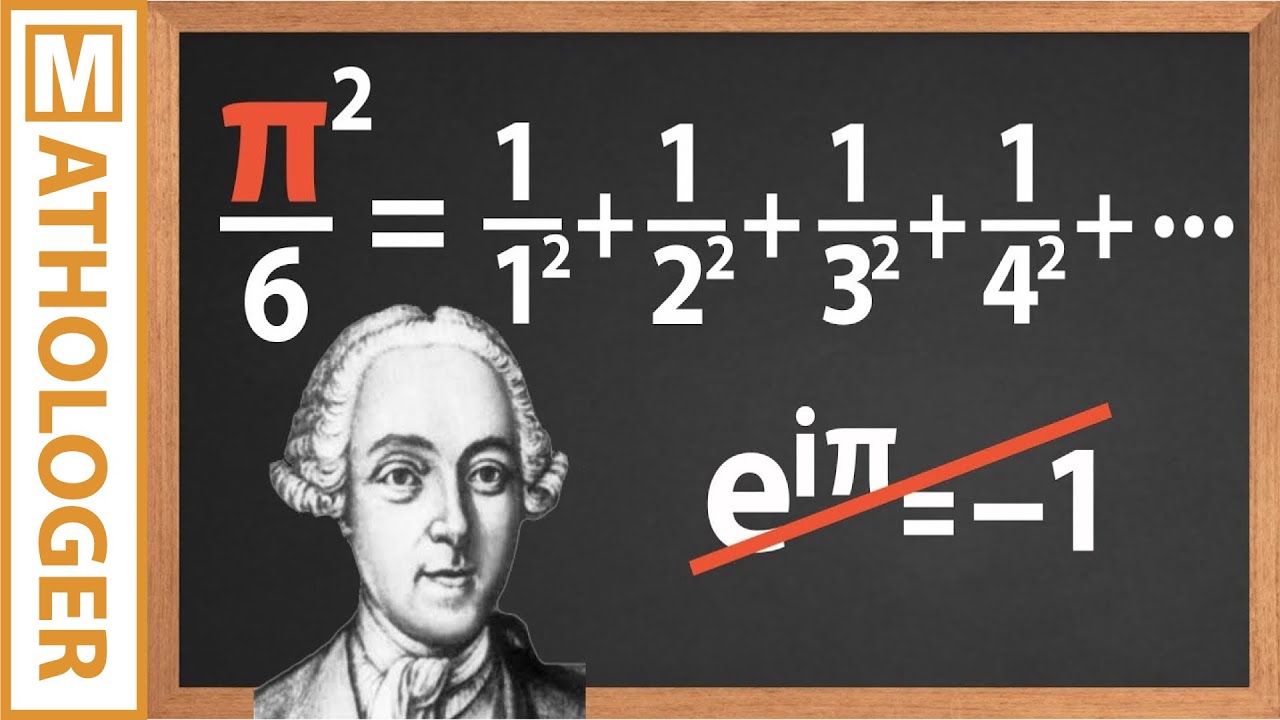The Wallis product for pi, proved geometrically
TLDRThis script explores the Wallace product, an intriguing mathematical relationship between an infinite series of fractions and the geometry of circles, specifically pi. It introduces a novel proof of this connection, discovered by 3Blue1Brown's new member, Sweeter. The proof uses geometric concepts and complex numbers to demonstrate that the product of fractions converges to pi/2. The script also generalizes the concept to express sine as an infinite product, revealing deep connections between mathematical formulas and concepts.
Takeaways
- 📚 The video introduces a novel proof of the Wallace product, an infinite product for pi, which is a lesser-known but significant mathematical result.
- 🌐 The Wallace product connects a series of fractions with the geometry of circles, specifically the concept of pi, through a multiplication process rather than addition.
- 🔍 The proof involves a unique approach that diverges from traditional methods, offering a fresh perspective on a well-established mathematical concept.
- 🎨 The video's creation process was different from usual, with the new 3Blue1Brown member, Sweeter, contributing to the development of the proof.
- 🔢 The series starts with a simple product of fractions, alternating between even numerators and odd denominators, which converges to pi/2.
- 🏖 The explanation takes a detour into geometric tools, using a circle with evenly spaced points and a special point to visualize the mathematical concepts.
- 💡 Two key lemmas are central to the proof: one about the distance product when the observer is midway between two points, and another when the observer replaces one of the points.
- 📈 The use of complex numbers and roots of unity simplifies the computation of the distance product, leveraging the symmetry of the unit circle in the complex plane.
- 🔄 The proof relies on the interchange of limits in infinitary arithmetic, which is justified by the dominated convergence theorem, ensuring the rigor of the argument.
- 🚀 The final result is a surprising connection: the infinite product of the series equals pi/2, a fact named after 17th-century mathematician John Wallace.
- ✨ The proof not only confirms the Wallace product but also generalizes to provide a formula for the sine function as an infinite product, showing deep connections between various mathematical formulas.
Q & A
What is the main topic of the video script?
-The main topic of the video script is the Wallace product, an infinite product for pi, and its surprising connection to the geometry of circles.
What makes the Wallace product unique compared to other mathematical results?
-The Wallace product is unique because it involves multiplying fractions rather than adding them up, which is a different approach to revealing connections between mathematical sequences and geometric shapes like circles.
Why is the Wallace product video special for 3Blue1Brown?
-The Wallace product video is special for 3Blue1Brown because it presents, to their knowledge, a more original proof of the Wallace product, which is a well-known mathematical result.
Who is credited with the original discovery of the Wallace product?
-17th-century mathematician John Wallace is credited with the original discovery of the Wallace product.
What geometric setup is used to explain the connection between the Wallace product and pi?
-The geometric setup involves a circle with many evenly spaced points around it and one additional special point, which is used to explore the distance product for an observer in relation to these points.
What are the two key facts or lemmas used in the proof of the Wallace product?
-The two key facts are: 1) If the observer is positioned halfway between two lighthouses on the circle, the distance product is exactly 2. 2) If one lighthouse is removed and the observer takes its place, the distance product equals the number of remaining lighthouses.
How does the video script connect the geometric properties of points on a circle to algebraic properties?
-The script connects geometric properties to algebraic properties by considering the points on the unit circle in the complex plane, using the roots of unity and their algebraic representations to simplify the calculation of the distance product.
What is the significance of the chord of f in the script?
-The chord of f is significant as it represents the length of a cord corresponding to a fraction f of a unit circle, which is used to simplify the calculation of the distance product for an observer at different positions on the circle.
How does the video script generalize the discussion to include a product formula for sine?
-The script generalizes the discussion by considering the distance product for an observer at any fraction f of the way between two lighthouses, leading to an infinite product that expresses sine of x in terms of pi and the product of terms involving f and k.
What mathematical concept is used to justify the interchange of limits in the argument presented in the script?
-The mathematical concept used to justify the interchange of limits is the dominated convergence theorem, which ensures that the argument holds under certain conditions.
What is the importance of the one-for-one combination of terms in the infinite product for pi?
-The one-for-one combination of terms is crucial because it ensures the convergence of the product to pi divided by 2. Intermixing the terms differently could yield different results.
How can the sine of x be expressed as an infinite product according to the script?
-According to the script, the sine of x can be expressed as an infinite product involving the product of (1 - f/k) over all non-zero integers k, where f is the fraction of the way between lighthouses, and this product equals f times pi divided by the sine of f times pi.
Outlines
🔍 Introduction to the Wallace Product and Circle Geometry
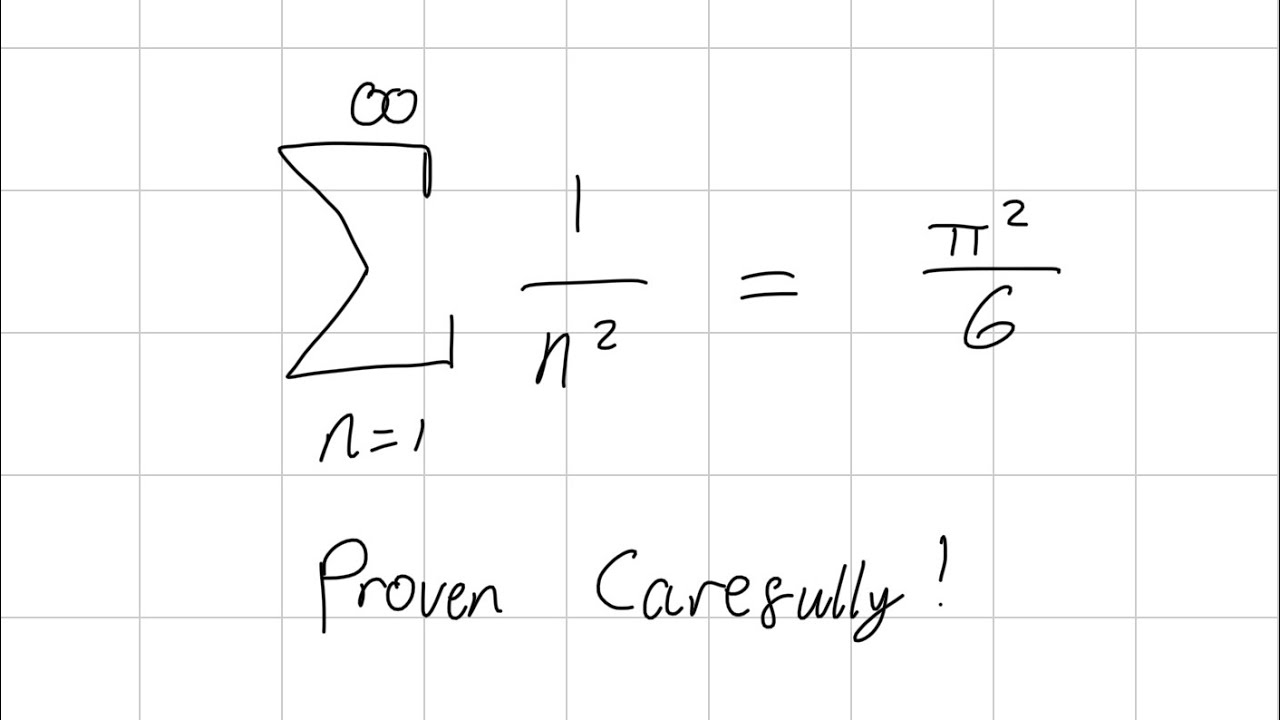
The script introduces a fascinating mathematical exploration that uncovers an unexpected link between a sequence of fractions and the geometry of circles. This video from 3Blue1Brown is unique as it presents an original proof of the Wallace product, a well-known mathematical formula for pi. The proof involves a novel approach to multiplying fractions in a series, which intriguingly converges to pi divided by 2. The video promises to delve into geometric tools and concepts to establish this connection, starting with the setup of a circle with evenly spaced points and a special observer point, reminiscent of the Basel problem discussed in a previous video.
📚 Geometric Tools and the Distance Product
This paragraph delves into the geometric tools necessary for understanding the proof of the Wallace product. It introduces the concept of a distance product, which is a multiplication of distances between a special point (observer) and multiple points (lighthouses) evenly distributed around a circle. Two key lemmas are highlighted: first, that the distance product for an observer halfway between two lighthouses is exactly 2; and second, that removing one lighthouse and placing the observer there results in a distance product equal to the total number of lighthouses. The paragraph also introduces the algebraic properties of these points when considered as complex numbers on the unit circle, known as roots of unity, and how they relate to the geometric setup.
🧩 Complex Numbers and the Simplification of Distance Product
The script explains how the geometric arrangement of points on a circle translates into an algebraic simplification when viewed through the lens of complex numbers. By considering the points as roots of unity on the complex plane, the multiplication of distances (the distance product) can be simplified using the properties of complex numbers. The roots of unity are shown to be related to polynomial equations, which simplifies the computation of the distance product. The concept of 'cord of f' is introduced as a function to represent the length of a chord corresponding to a fraction of the circle's circumference, which simplifies the expression of the distance product for various observer positions.
🌐 The Wallace Product and Its Relation to Pi
The script presents the Wallace product, an infinite product that converges to pi divided by 2, and connects it to the geometric setup involving lighthouses and an observer. It describes a scenario with two observers, a 'keeper' on a lighthouse and a 'sailor' halfway between lighthouses, and explores the ratio of their respective distance products. The paragraph explains how, as the number of lighthouses increases, the contributions from each lighthouse can be approximated, leading to the convergence of the product to pi divided by 2. The proof involves considering the angles and distances between the observers and the lighthouses, and how these relationships change as the number of lighthouses becomes very large.
🔄 The Commuting of Limits and Generalization to Sine
The final paragraph discusses the mathematical subtleties of commuting limits in the context of infinite products and sums. It points out that the product of limits does not always equal the limit of products, especially with an infinite number of terms. However, the dominated convergence theorem assures the validity of the argument presented in the video. The script also generalizes the discussion to express the sine function as an infinite product, connecting the proof of the Wallace product to Euler's original solution to the Basel problem. This broader perspective reveals deeper connections between formulas for pi and the sine function, showcasing the beauty and interconnectedness of mathematical concepts.
Mindmap
Keywords
💡3Blue1Brown
💡Wallace Product
💡Infinite Product
💡Geometry of Circles
💡Roots of Unity
💡Complex Numbers
💡Sine Function
💡Dominated Convergence
💡Chord
💡Sine Product Formula
Highlights
Introduction of a new, original proof of the Wallace product, an infinite product for pi.
The Wallace product involves multiplying fractions in a specific pattern, unlike traditional addition-based series.
The video's unique production process, stemming from independent discovery and proof by a 3Blue1Brown member.
Exploration of the mathematical value of presentation through the combination of underlying math and communication choices.
The surprising connection between the Wallace product and the geometry of circles.
The product's initial form, involving even numerators and odd denominators, and its divergence to infinity.
A contrasting series with fractions less than one, converging towards zero.
The innovative mixing of the two series to create a new product that converges to a finite value.
The revelation that the mixed product converges to pi divided by 2.
Introduction of geometric tools and the setup involving a circle with evenly spaced points and a special point.
The use of complex numbers and roots of unity to simplify the calculation of the distance product.
Two key lemmas about the distance product when the observer is positioned at specific points on the circle.
The algebraic property of evenly spaced points on a circle corresponding to the roots of unity in the complex plane.
The simplification of the distance product calculation using complex polynomials.
The definition of a special function 'cord of f' to represent the length of a cord on a unit circle.
The application of the key facts to understand the relationship between the product and pi.
The generalization of the proof to express sine of x as an infinite product.
The connection between the Wallace product and Euler's original solution to the Basel problem.
The importance of the dominated convergence theorem in justifying the commuting of limits in the proof.
The technical consideration of the product's convergence and the conditions under which it equals pi divided by 2.
A supplementary blog post for further details and a deeper understanding of the proof.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: