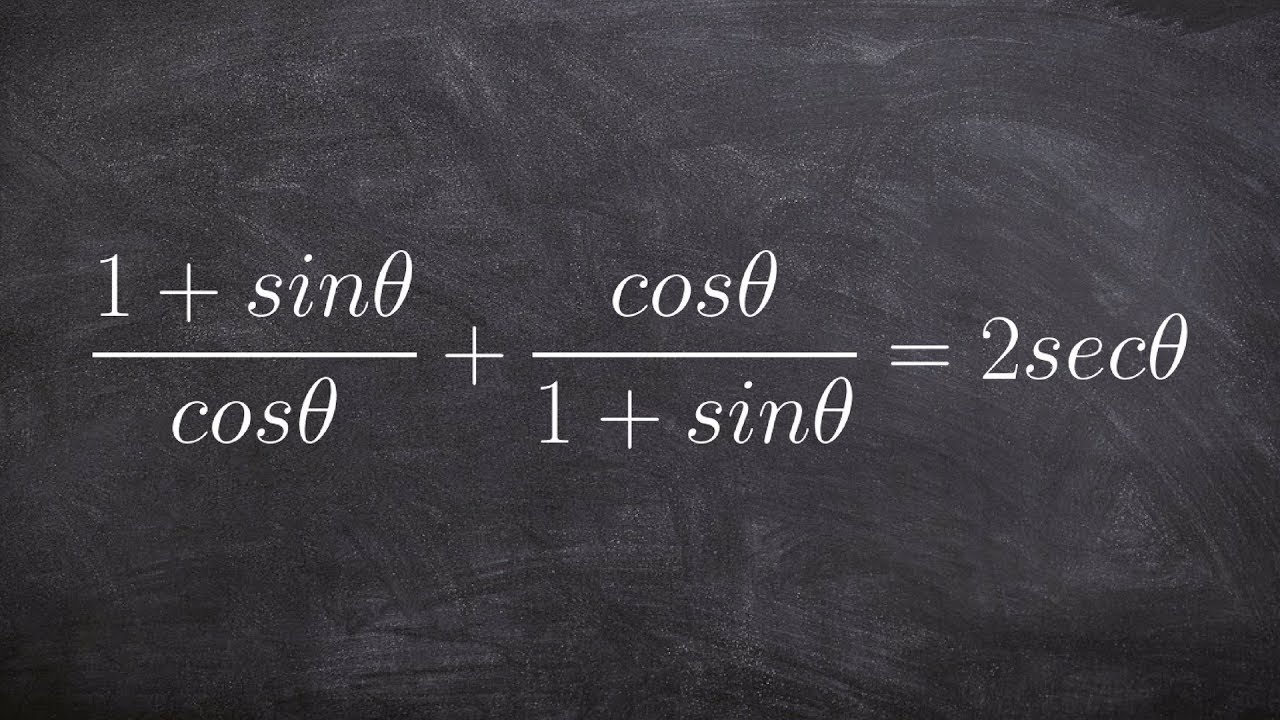Pythagoras twisted squares: Why did they not teach you any of this in school?

Mathologer

15 Oct 202238:32

EducationalLearning

32 Likes 10 Comments

TLDRThis Mathologer video delves into the Pythagorean theorem's lesser-known aspects, showcasing creative visual proofs and intriguing mathematical secrets. It revisits the classic A^2 + B^2 = C^2, explores ancient Chinese manuscripts, and introduces the concept of Pythagorean triples. The video also presents Fermat's four square theorem, Trithagorean theorems for 60-degree and 120-degree triangles, and a variety of geometric identities. Additionally, it covers the application of twisted square diagrams to derive inequalities and trigonometric identities, as well as the fascinating 'bug chasing' problem, offering a rich exploration of mathematical history and geometry.

Takeaways

📚 The video discusses the iconic twisted square diagram associated with Pythagoras' theorem, revealing lesser-known secrets and proofs.
🔍 It provides a visual proof of Pythagoras' theorem using four copies of a right-angled triangle to form a large square, demonstrating that the area of the large square equals the sum of the areas of the four smaller squares.
🎯 The script introduces an alternative algebraic proof involving the area of the large square, the small square, and the four right-angled triangles, leading to the same fundamental theorem.
🌐 The video mentions the historical aspect of the twisted square diagram, which has been part of mathematical proofs for thousands of years and is featured in ancient Chinese manuscripts.
📉 It explores the concept of Pythagorean triples and their relation to the squares within the twisted square diagram, highlighting the integer solutions to the theorem.
🧩 The script delves into Fermat's four square theorem, which posits that there cannot be four squares in an arithmetic progression, a discovery attributed to Pierre de Fermat.
📐 The video presents a Trithagorean theorem for 60-degree triangles, which is a variant of Pythagoras' theorem adapted for non-right-angled triangles.
🤔 It asks viewers to consider the implications of the Trithagorean theorem and whether there are integer-sided triangles that satisfy the theorem, introducing the concept of Eisenstein triples.
🔄 The script describes a 'bug chasing vortex' problem, where bugs on the corners of a square move towards each other, leading to a discussion on the paths and equations governing their movement.
📉 The video touches on various mathematical inequalities and identities, such as the geometric mean-arithmetic mean inequality and the Cauchy-Schwarz inequality, using the twisted square diagram as a visual aid.
🎨 The final segment of the script offers a puzzle related to the twisted square diagram with overlapping triangles, inviting viewers to calculate the area of a central square given certain values of A and B.

Q & A

What is the fundamental principle illustrated by the iconic twisted square diagram?
-The twisted square diagram illustrates the Pythagorean theorem, which states that in a right-angled triangle with sides A and B and hypotenuse C, the area of the square on the hypotenuse (C squared) is equal to the combined area of the squares on the two shorter sides (A squared plus B squared).
How does the visual proof of the Pythagorean theorem using four copies of a right-angled triangle work?
-The visual proof involves arranging four copies of the right-angled triangle to form a large square. The area not covered by the triangles is C squared. By rearranging the triangles within the square without overlap, it's shown that this area can also be expressed as A squared plus B squared, thus proving the Pythagorean theorem.
What is the significance of the 3-4-5 right-angled triangle in the context of Pythagorean triples?
-The 3-4-5 triangle is a prototype Pythagorean triple, meaning it is a set of three positive integers that satisfy the equation A squared plus B squared equals C squared. It is one of the most well-known and fundamental examples of such triples.
What is Fermat's Last Theorem, and how does it relate to Pythagorean triples?
-Fermat's Last Theorem states that there are no three positive integers A, B, and C that satisfy the equation A^n + B^n = C^n for any integer value of n greater than 2. This highlights the rarity of Pythagorean triples, which are integer solutions to the equation for n=2.
What is the Trithagorean theorem for 60-degree triangles, and how does it differ from the Pythagorean theorem?
-The Trithagorean theorem for 60-degree triangles states that the sum of the areas of two equilateral triangles with sides A and B is equal to the area of an equilateral triangle with side C, plus a correction term which is the area of the original triangle with sides A and B. This differs from the Pythagorean theorem by including a correction term that accounts for the geometry of 60-degree triangles.
What is the connection between Pythagorean triples and arithmetic progressions of squares?
-Pythagorean triples correspond to three squares that are in an arithmetic progression of length 3. For example, the triple 3, 4, 5 corresponds to the squares 1, 9, and 25, which are in arithmetic progression with a common difference of 8.
What is Fermat's four square theorem, and what does it state?
-Fermat's four square theorem is a result that states any integer can be represented as the sum of four squares. It is related to the observation that certain Pythagorean triples can be associated with three squares in an arithmetic progression, and it extends this idea to four squares.
How do the twisted square diagrams relate to the geometric mean and arithmetic mean inequality?
-The twisted square diagrams can be used to demonstrate that the geometric mean of two positive numbers is always less than or equal to their arithmetic mean. This is shown by comparing the areas of shapes formed by the sides of the square and rectangles within the diagram.
What is the Hexagorean theorem, and how is it derived from the twisted square diagrams?
-The Hexagorean theorem is a humorous term used in the script to describe a property of regular hexagons related to 120-degree triangles. It is derived by dividing the twisted square diagrams for 120-degree triangles by 6, showing that the area of a regular hexagon can be expressed in terms of the areas of 120-degree triangles.
What is the significance of the bugs chasing each other in a square, and what does it reveal about their paths?
-The bugs chasing each other in a square is a thought experiment that leads to surprising conclusions about their paths. It reveals that the bugs will circle the center infinitely often, but their paths will always be of finite length, specifically related to the side length of the square.
How does the twisted square diagram relate to the addition formula for sine, and how is it demonstrated?
-The twisted square diagram can be modified to represent a situation involving angles and sines. By adjusting the diagram so that all sides of a parallelogram are equal to 1 and considering the areas of the blue regions in terms of these angles, the addition formula for sine emerges as a result of the arrangement of the triangles and parallelogram.

Outlines

00:00

📐 Introduction to the Pythagorean Theorem

The script begins with an introduction to the Pythagorean theorem, a fundamental principle in mathematics relating the sides of a right-angled triangle. The presenter uses a visual diagram, which is also part of the Mathologer logo, to explain the theorem. They provide a classic visual proof involving four copies of a right-angled triangle arranged to form a larger square, demonstrating that the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the other two sides. The script also mentions that there are more secrets to this diagram that even many professional mathematicians may not be aware of, setting the stage for a deeper exploration of the theorem and its implications.

05:01

🔍 Deep Dive into Pythagorean Triples and Chinese Proofs

This paragraph delves into the history and variations of the Pythagorean theorem, including the Chinese manuscript that features an early proof. It discusses the concept of Pythagorean triples, sets of three positive integers that fit the theorem, with 3-4-5 being a well-known example. The script also touches on Fermat's last theorem, which states that there are no integer solutions for the equation A^n + B^n = C^n for n>2, contrasting with the existence of Pythagorean triples. The Chinese drawing with a grid is used to illustrate the generality of the theorem and the special case of the 3-4-5 triple. The paragraph concludes with an exploration of the arithmetic progressions within squares, known to Fermat, and the impossibility of longer sequences of squares in arithmetic progression, a result that Fermat is believed to have proven but without a known record of the proof.

10:05

🦗 Exploring the TRIthagorean Theorem and Equilateral Triangles

The script presents a novel theorem, the TRIthagorean theorem, which is an extension of the Pythagorean theorem to equilateral triangles with a 60-degree angle. It describes a visual proof involving the arrangement of triangles to form larger equilateral triangles and the subsequent shuffling of these triangles to reveal a relationship between their areas. The presenter also discusses the Trithagorean theorem for 60-degree triangles, which includes a correction term, and its counterpart for 120-degree triangles. The paragraph concludes with the discovery of integer-sided triangles that fit these theorems, known as Eisenstein triples, and the potential for using these in a new Mathologer logo.

15:09

🔄 The Hexagorean Theorem and Twisted Squares

This paragraph introduces the concept of the Hexagorean theorem, which is related to the arrangement of 12 equilateral triangles to form a larger shape. The presenter uses a modified twisted square diagram to explore this theorem and its connection to the Trithagorean theorem for 120-degree triangles. The script also discusses the visual appeal of these mathematical proofs and the surprising insights they provide into the properties of triangles and squares. The paragraph concludes with a puzzle involving a third type of twisted square diagram and a challenge for the audience to calculate the area of a central square given specific side lengths.

20:13

🐛 The Bug Chasing Vortex and Unexpected Mathematical Explorations

The script presents a thought experiment involving bugs running towards each other on the sides of a square, a problem popularized by Martin Gardner. It explores the paths the bugs would take, the equations describing their motion, and the surprising outcomes of their journey. The presenter uses twisted square diagrams to provide insight into the problem and to demonstrate that the paths of the bugs would be of finite length, despite appearing to wind around the center infinitely. The paragraph concludes with a detailed explanation of the geometric series involved in calculating the total length of a bug's path and a discussion of the implications of changing the fraction of the side length covered by the bugs.

25:15

📚 Concluding Thoughts and Additional Mathematical Insights

In the final paragraph, the presenter reflects on the various mathematical concepts and proofs discussed in the script, from the Pythagorean theorem to the bug chasing vortex. They invite the audience to explore further details through provided links and pose a final puzzle involving a third type of twisted square diagram. The script concludes with an animated proof of the Cauchy-Schwarz inequality and an invitation for the audience to share their thoughts and solutions in the comments section.

Mindmap

Keywords

💡Pythagorean Theorem

The Pythagorean Theorem is a fundamental principle in geometry that states in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This theorem is central to the video's theme, as it is the basis for the various proofs and mathematical explorations presented. For example, the script discusses the theorem's application in different visual proofs involving squares and triangles.

💡Right-Angled Triangle

A right-angled triangle is a type of triangle that has one angle that is exactly 90 degrees. This concept is integral to the video's content as it is the foundation for understanding the Pythagorean Theorem. The script uses right-angled triangles to demonstrate the theorem and its various proofs, such as the one involving the rearrangement of four copies of a right-angled triangle into a larger square.

💡Algebraic Proof

An algebraic proof is a method of proving a mathematical statement using algebraic manipulation and logical reasoning. In the context of the video, the script refers to an algebraic proof of the Pythagorean Theorem, where areas of shapes are expressed algebraically, and the theorem is derived through algebraic simplification. This type of proof is contrasted with a visual or geometric proof.

💡Visual Proof

A visual proof is a method of demonstrating a mathematical theorem using geometric figures and their properties, often involving the manipulation of shapes to show the equality of areas or lengths. The video script provides several examples of visual proofs for the Pythagorean Theorem, such as rearranging triangles to form squares and using these configurations to demonstrate the theorem's validity.

💡Fermat's Four Square Theorem

Fermat's Four Square Theorem is a result in number theory that states four squares can be expressed as the sum of two squares in exactly the same way that two squares can be expressed as the sum of two squares, as in the Pythagorean Theorem. The script mentions this theorem as part of the broader exploration of the properties of squares and their relationships to other mathematical concepts.

💡Arithmetic Progression

An arithmetic progression is a sequence of numbers in which the difference between consecutive terms is constant. In the video, the concept is used to describe sequences of squares that have a common difference, which is a key element in Fermat's exploration of squares and is related to the Pythagorean triples discussed in the script.

💡Pythagorean Triple

A Pythagorean triple consists of three positive integers a, b, and c, such that a² + b² = c², which are the lengths of the sides of a right-angled triangle. The script discusses the significance of Pythagorean triples in the context of the theorem and how they can be visualized and proven using the twisted square diagrams.

💡Eisenstein Triples

Eisenstein triples are a set of three integers that satisfy a particular equation related to equilateral triangles, analogous to Pythagorean triples but for 60-degree triangles. The script introduces this concept as part of the exploration of generalizations of the Pythagorean Theorem to other types of triangles.

💡Trithagorean Theorem

The Trithagorean theorem is a generalization of the Pythagorean Theorem for 60-degree and 120-degree triangles, introduced in the script as a way to extend the classical theorem to other geometric configurations. The theorem is used to derive relationships between the sides of these triangles and their corresponding areas.

💡Inequality

In mathematics, an inequality is a relation that holds between two expressions when one is greater than, less than, or not equal to the other. The script discusses inequalities such as the geometric mean being less than or equal to the arithmetic mean, and the Cauchy-Schwarz inequality, using geometric configurations to illustrate these relationships.

💡Geometric Mean

The geometric mean of a set of numbers is a measure of central tendency that indicates the central or typical value in a set of numbers whose product is known. In the script, the geometric mean is used in the context of inequalities and is shown to be always less than or equal to the arithmetic mean through a visual geometric proof.

💡Cauchy-Schwarz Inequality

The Cauchy-Schwarz inequality is a statement in mathematics that establishes a maximum possible value for the dot product of two vectors, given their lengths. The script mentions this inequality as an example of a mathematical concept that can be visually demonstrated using geometric configurations similar to those used in the proofs of the Pythagorean Theorem.

💡Bug Chasing Vortex

The bug chasing vortex is a thought experiment or mathematical puzzle involving bugs moving towards each other on the sides of a square or other shapes. The script uses this concept to explore interesting mathematical properties related to motion, distance, and angles, and to illustrate unexpected outcomes in geometric configurations.

Highlights

Introduction to the iconic twisted square diagram and its association with Pythagoras' theorem.

Visual proof of Pythagoras' theorem using four copies of a right-angled triangle.

Demonstration of the area of a large square being equal to the sum of the areas of four triangles and a smaller square.

Exploration of the algebraic proof of Pythagoras' theorem involving the area of triangles and squares.

Historical context of the twisted square diagram in ancient Chinese manuscripts.

Introduction of Fermat's four square theorem and its relation to Pythagorean triples.

Explanation of the existence of Pythagorean triples and their significance in mathematics.

Discovery of arithmetic progressions within square numbers related to Pythagorean triples.

Fermat's last theorem and its implications for integer solutions in equations.

Introduction of the Trithagorean theorem for 60-degree triangles and its proof.

Generalization of Pythagoras' theorem to equilateral triangles and other shapes.

Presentation of the Hexagorean theorem and its relation to the Trithagorean theorem.

Discussion of the geometric mean and arithmetic mean inequality using twisted square diagrams.

Derivation of the Cauchy-Schwarz inequality through geometric illustrations.

Application of twisted square diagrams to the addition formula for sine in trigonometry.

Engagement with the 'bug chasing vortex' problem popularized by Martin Gardner.

Analysis of the infinite series and geometric progression in the context of the bug chasing problem.

Final puzzle involving a third type of twisted square diagram with overlapping triangles.

Transcripts

Browse More Related Video

Special Patterns of the Pythagorean Theorem For Right Triangles

03 - Pythagorean Trig Identities, Part 1

Proving the Pythagorean Theorem

Fibonacci = Pythagoras: Help save a beautiful discovery from oblivion

Verifying a trigonometric Identities

Lec 28 | MIT 18.01 Single Variable Calculus, Fall 2007

Related Tags

Pythagoras Theorem Mathematical Proofs Twisted Squares Trithagorean Identity Fermat's Theorem Eisenstein Triples Mathologer Geometry Puzzles Educational Content Mathematical Exploration