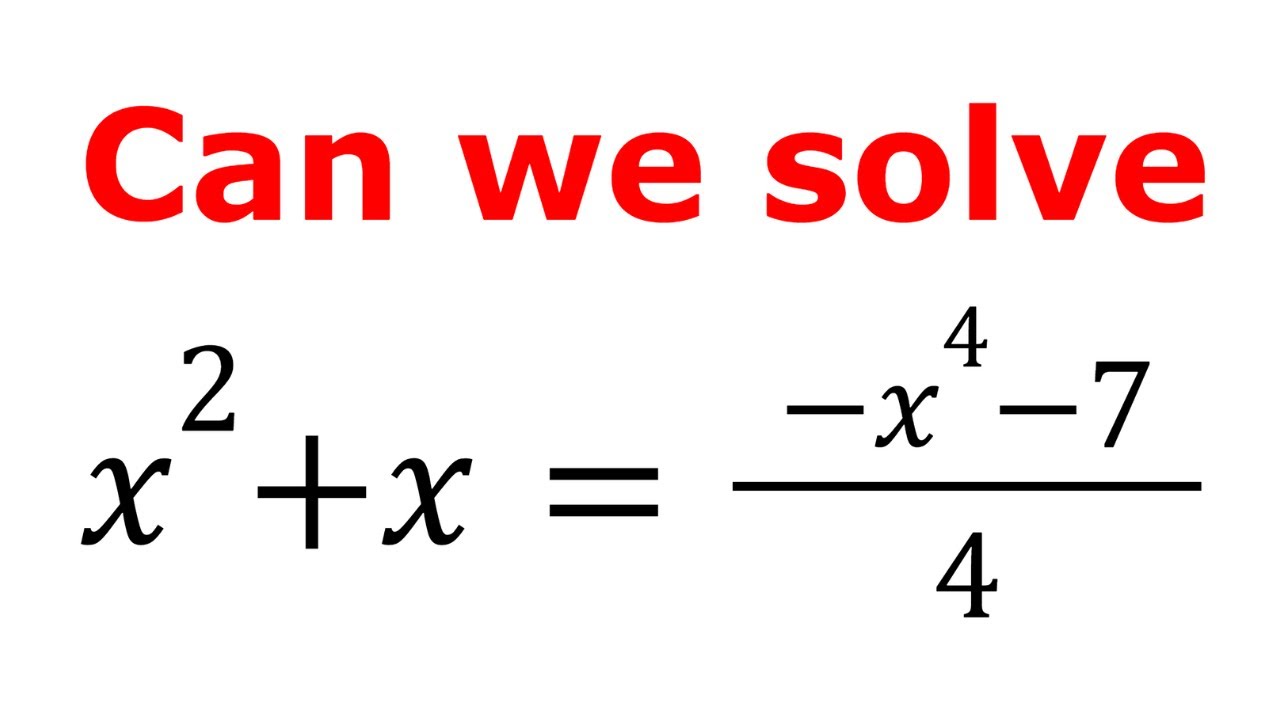A Cool Radical Equation | Math Olympiads

SyberMath
29 Jun 202309:49
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the presenter tackles a radical equation involving a square root and polynomial expressions. Initially, they introduce a brute force method by squaring both sides of the equation, which leads to a quartic equation. They caution about the potential for extraneous solutions when dealing with even powers. The presenter then opts for a more elegant approach, leveraging the vertex form of a parabola and properties of a semi-circle to deduce that the equation has no real solutions. The video concludes with a graphical analysis that confirms the absence of real solutions, providing a clear and visual explanation. The presenter encourages viewers to engage with the content and look forward to future videos.

Takeaways
  • 📚 The video is about solving a radical equation involving a polynomial and a square root on the right-hand side.
  • 🔍 Two methods are introduced to solve the equation: a brute force approach and a more insightful geometric method.
  • 🔢 The brute force method involves squaring both sides of the equation to eliminate the square root, which can introduce extraneous solutions.
  • 📐 The geometric method leverages the properties of parabolas and semi-circles to find potential solutions by analyzing their intersections.
  • 📉 Squaring both sides can lead to a quartic equation, which is complex and may not have real solutions due to the nature of even powers.
  • ❗ The importance of avoiding extraneous solutions when solving equations by squaring is highlighted.
  • 📈 The vertex form of a parabola is used to simplify the problem and find the vertex, which is crucial for understanding the graph's behavior.
  • 🔍 The video emphasizes the significance of understanding the properties of functions and their graphs in solving equations.
  • 🚫 The script reveals that the potential solution x = -1 does not satisfy the original equation, indicating the need for careful verification.
  • 📊 The graph of the functions shows that they do not intersect, suggesting there are no real solutions to the equation.
  • 👋 The video concludes with a reminder to engage with the content through comments, likes, and subscriptions, and a teaser for the next video on a functional equation.
Q & A

  • What is the main equation being solved in the video?

    -The main equation being solved is x^2 + 2x + 3 = √(4 - x^2).

  • What is the first method introduced to solve the equation?

    -The first method introduced is to square both sides of the equation to eliminate the square root.

  • Why is there a risk when squaring both sides of an equation?

    -Squaring both sides can introduce extraneous solutions, which are solutions that do not satisfy the original equation but appear due to the squaring process.

  • What is the issue with the cubic term in the equation after squaring both sides?

    -The issue is that squaring both sides leads to a quartic (fourth-degree) equation, which is more complex to solve and may not have real solutions.

  • What is the second method presented in the video?

    -The second method involves rewriting the equation in vertex form to take advantage of the properties of parabolas and semi-circles.

  • How does the vertex form help in solving the equation?

    -The vertex form provides the vertex of the parabola, which can help in understanding the maximum or minimum value of the function and the behavior of the parabola.

  • What is the conclusion about the real solutions of the given equation?

    -The conclusion is that there are no real solutions to the equation because the functions do not intersect at the same x-coordinate for the y-value of 2.

  • Why are odd-powered equations like cubics guaranteed to have at least one real solution?

    -Odd-powered equations have at least one real solution because they must have a linear factor, which corresponds to a real root.

  • What is the significance of the coefficient of x^3 being divided by the degree?

    -Dividing the coefficient of x^3 by the degree (which is 4 in this case) helps to eliminate the cubic term from the equation, simplifying it.

  • How does the video use the properties of a semi-circle in the second method?

    -The video uses the fact that the square root of (4 - x^2) is always less than or equal to 2, which helps to establish the conditions for the equality in the equation.

  • What is the final advice given to viewers regarding solving such equations?

    -The final advice is to not just use brute force in a real test situation, but to look for alternative methods that can simplify the process and make it easier to find the solution.

  • Why is the graph of the situation considered interesting in the video?

    -The graph is interesting because it shows that the functions attain the y-value of 2 at different x-coordinates, which is why they do not intersect and why there are no real solutions.

Outlines
00:00
🧮 Solving Radical Equations: Initial Approach

In this video, we tackle solving a radical equation involving the square root of 4 minus x squared on the right-hand side, while the left-hand side is a polynomial. The goal is to find the x values that satisfy this equation. We explore two methods, starting with squaring both sides of the equation, but caution against introducing extraneous solutions. The first method involves expanding the equation and simplifying it to a quartic equation, highlighting the complexity and potential pitfalls of this approach.

05:00
🔍 Alternative and Efficient Method

The second method focuses on a more elegant approach by rewriting the equation in vertex form to identify the behavior of the parabola and the semicircle. This method highlights the importance of the vertex form in understanding the maximum or minimum values of the function. By comparing the values, it is determined that the equation has no real solutions, which is further illustrated with a graph to explain why the functions do not intersect at any point. This method showcases a more conceptual understanding rather than brute force algebra.

Mindmap
Keywords
💡Radical Equation
A radical equation is a mathematical equation that includes at least one radical expression, such as a square root. In the video, the equation x^2 + 2x + 3 = √(4 - x^2) is an example of a radical equation. The theme revolves around solving this type of equation, which is central to the video's educational content.
💡Polynomial
A polynomial is an algebraic expression made up of variables and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. In the script, the terms x^2 and 2x are parts of a polynomial on the left side of the equation.
💡Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. In the context of the video, the square root symbol (√) is used to denote the radical part of the equation, specifically √(4 - x^2), which is a key component in the equation to be solved.
💡Extraneous Solutions
Extraneous solutions are values that may appear to be solutions after certain algebraic manipulations, such as squaring both sides of an equation, but do not actually satisfy the original equation. The script warns about the potential for extraneous solutions when dealing with radical equations, emphasizing the importance of verifying solutions.
💡Squaring Both Sides
Squaring both sides of an equation is a common algebraic technique used to eliminate square roots or other radicals. In the video, the presenter initially squares both sides of the radical equation to simplify it, which is a pivotal step in the first method of solving the equation presented.
💡Quartic Equation
A quartic equation is a polynomial equation of degree four. After squaring both sides of the original radical equation, the presenter ends up with a quartic equation, which is more complex to solve than lower-degree polynomials. The script discusses the complexity of solving quartic equations and their potential lack of real solutions.
💡Vertex Form
Vertex form is a way of writing a quadratic equation that makes it easy to identify the vertex of the parabola represented by the equation. In the video, the presenter rewrites part of the equation in vertex form to leverage its properties in solving the equation, which is a key step in the second method.
💡Parabola
A parabola is the set of all points that are equidistant from a fixed point (the focus) and a line (the directrix). The video script discusses the properties of a parabola in the context of the equation x^2 + 2x + 3, which represents a parabola opening upwards.
💡Semi-Circle
A semi-circle refers to half of a circle. In the script, the presenter uses the term to describe the graph of √(4 - x^2), which represents a semi-circle because the equation is equivalent to the square root of the difference between a constant and a squared term.
💡Graph
A graph is a visual representation of data, typically used to plot the points of a function. The video script mentions the importance of graphing the equation to understand the relationship between the parabola and the semi-circle, and to illustrate why there are no real solutions to the equation.
💡Real Solutions
Real solutions are values that, when substituted into the original equation, satisfy the equation and make the equation true. The video concludes by discussing the absence of real solutions for the given radical equation, which is a significant outcome of the problem-solving process.
Highlights

Introduction to solving a radical equation involving square roots and polynomials.

Two methods will be discussed to find the X values of the equation.

The first method involves brute forcing the equation by squaring both sides.

Risk of introducing extraneous solutions when squaring both sides.

Explanation of extraneous solutions and their implications.

Using the formula for squaring a binomial to simplify the equation.

Transformation of the equation into a quartic equation.

Discussion on the complexity of solving quartic equations.

Mention of the QWERTY formula and its impracticality for large screens.

The importance of understanding the behavior of odd and even powered equations.

Introduction of the second method as an alternative to brute force.

Observation that the equation resembles a semi-circle and a parabola.

Use of the vertex form to simplify the equation and find the vertex.

Analysis of the equation's behavior and the significance of the value 2.

Realization that the equation has no real solutions due to different X coordinates.

Visualization of the problem through a graph to understand the lack of intersection.

Conclusion that there are no real solutions to the given radical equation.

Invitation for viewers to comment, like, and subscribe for more content.

Transcripts

Browse More Related Video

Solving A Quartic | Two Methods

Evaluating A Radical Expression | Two Methods

You wouldn’t expect this "quadratic" equation to have 6 solutions!

The Algebra Step that EVERYONE Gets WRONG!

Solving Quadratic Equations With Exponents

Can We Solve A Nice Factorial Equation

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Radical EquationsAlgebra TechniquesGraph AnalysisMath EducationEquation SolvingPolynomial FunctionsSquare RootVertex FormNo Real SolutionsMath Olympiad