How to find the component form of a vector

Brian McLogan
7 Mar 201305:03
EducationalLearning
32 Likes 10 Comments

TLDRThe video script provides an insightful look into the concept of vectors on a plane, particularly within the Cartesian coordinate system. It starts by introducing a vector without any specific context and then places it within the Cartesian system to discuss its coordinates, denoted as points P and Q with respective x and y values. The script emphasizes the importance of standard forms in equations for solving various problems, drawing parallels to how vectors can be represented in a standardized way. The core concept discussed is finding the component form of a vector, which is illustrated through the subtraction of coordinates of the initial point (P1, P2) from the terminal point (Q1, Q2). A practical example is given to demonstrate how to calculate this component form, resulting in a simplified representation that starts at the origin (0,0) and extends to the terminal point. The video concludes by highlighting the utility of component form in analyzing vectors for their slope and magnitude, thus enabling a more systematic approach to vector analysis.

Takeaways
  • 📐 The concept of a vector is introduced as a directional segment on a plane that can be represented on a Cartesian coordinate system.
  • 📍 Vectors have two points: an initial point and a terminal point, which can be plotted on the Cartesian coordinate system as coordinates (x, y).
  • 🔍 When plotting a vector on the Cartesian coordinate system, the focus is on the x and y coordinates of the points P and Q.
  • 📌 Points P1 and P2 are used to represent the initial point, while Q1 and Q2 represent the terminal point of the vector.
  • 🧮 The component form of a vector is found by subtracting the coordinates of the initial point from the terminal point, resulting in the form (Q1 - P1, Q2 - P2).
  • 🌟 The component form simplifies the vector to two coordinates, which is helpful for standardization and comparison of vectors.
  • ➡️ The initial point in the component form is always at the origin (0, 0), which makes it easier to identify the terminal point by moving in the direction of the vector.
  • 📈 The component form allows for the analysis of the vector's slope and magnitude, even though it may not represent the exact vector visually.
  • 🔄 Re-representing a vector in its component form helps in understanding its direction and magnitude without the need for the actual initial and terminal points.
  • 🔢 The process of finding the component form involves simple arithmetic operations, making it a straightforward method to standardize vectors.
  • 🚀 The component form is particularly useful for mathematical operations and problem-solving involving vectors, as it provides a consistent format for all vectors.
Q & A

  • What is a vector?

    -A vector is a mathematical entity that has both magnitude and direction. It can be represented graphically as an arrow with a specific length and direction, and can be located anywhere on a plane.

  • What is the Cartesian coordinate system?

    -The Cartesian coordinate system is a two-dimensional coordinate system that specifies each point uniquely in a plane using an ordered pair of numbers (x, y), which represent the point's distances from the two coordinate axes.

  • How are the coordinates of a vector on a plane represented?

    -The coordinates of a vector on a plane are represented as an ordered pair (x, y), where 'x' is the horizontal component and 'y' is the vertical component of the vector.

  • What are the points P1 and P2 in the context of the script?

    -In the script, P1 and P2 are points on a plane that represent the initial and terminal points of a vector, respectively. They are used to define the vector's position in the Cartesian coordinate system.

  • What is the component form of a vector?

    -The component form of a vector is a representation that consists of the difference between the coordinates of the terminal point (Q1, Q2) and the initial point (P1, P2), expressed as (Q1 - P1, Q2 - P2).

  • Why is the component form of a vector useful?

    -The component form of a vector is useful because it simplifies the vector to its essential components, which are the differences in the x and y coordinates from the initial to the terminal point. This form allows for easier manipulation and analysis of vectors.

  • What does the initial point of a vector in component form represent?

    -In component form, the initial point of a vector is typically represented as the origin (0, 0), which simplifies the representation and allows for a standardized way of working with vectors.

  • How can you find the terminal point of a vector given its component form?

    -To find the terminal point of a vector given its component form, you add the components to the initial point coordinates (0, 0). For example, if the component form is (6, 7), the terminal point is (0+6, 0+7) or (6, 7).

  • What is the relationship between the slope and the component form of a vector?

    -The component form of a vector does not directly provide the slope, but it does give the change in the y-coordinate over the change in the x-coordinate, which is the definition of slope. By comparing the components, one can infer the slope of the vector.

  • Why might the script mention different forms of equations in the context of vectors?

    -The script mentions different forms of equations to draw an analogy between how vectors can be standardized in their representation (like component form) and how equations can be standardized in forms like standard form, slope-intercept form, or vertex form for easier problem-solving.

  • What is the magnitude of a vector in the context of the script?

    -The magnitude of a vector, while not explicitly defined in the script, is the length of the vector from its initial point to its terminal point. It is an important property of a vector that can be inferred from its component form.

  • Can you use the component form of a vector to determine its direction?

    -Yes, the component form of a vector can be used to determine its direction. The direction is indicated by the sign and magnitude of the components, which show how the vector is inclined relative to the coordinate axes.

Outlines
00:00
📐 Introduction to Vectors on a Plane

The video begins by introducing the concept of a vector on a plane, which can be located anywhere without the need for a specific coordinate system. The speaker then transitions to discussing vectors within the Cartesian coordinate system, emphasizing the importance of understanding the x and y coordinates of a vector's points, labeled as P1, P2 for the initial point and Q1, Q2 for the terminal point. The video sets the stage for further exploration into vector representation and calculations.

Mindmap
Keywords
💡Vector
A vector is a mathematical concept that has both magnitude and direction. In the context of the video, it is a directed line segment on a plane with an initial point and a terminal point. The video discusses vectors in relation to the Cartesian coordinate system, emphasizing their importance in various mathematical problems and their representation in component form.
💡Cartesian Coordinate System
The Cartesian coordinate system is a two-dimensional coordinate system that specifies each point uniquely in a plane using an ordered pair of numbers. These numbers, known as coordinates, are the x (horizontal) and y (vertical) values. The video uses this system to plot vectors and to find their component form.
💡Component Form
The component form of a vector is a representation that consists of its x and y components. It is denoted as V = <Q1 - P1, Q2 - P2>, where P1 and P2 are the coordinates of the initial point and Q1 and Q2 are the coordinates of the terminal point. The video explains that finding the component form simplifies the representation of a vector, making it easier to work with.
💡Initial Point
The initial point of a vector is the starting point from which the vector originates. In the video, the initial point is referred to as point P1 with coordinates (x, y). The concept is integral to understanding how vectors are defined and plotted on a coordinate system.
💡Terminal Point
The terminal point of a vector is the ending point where the vector terminates. In the video, the terminal point is referred to as point Q1 with coordinates (x, y). Together with the initial point, it defines the direction and magnitude of the vector.
💡Magnitude
The magnitude of a vector represents its length or size, which can be calculated using the distance formula from the initial point to the terminal point. In the video, the concept of magnitude is implied when discussing the representation of vectors and their properties.
💡Slope
The slope of a line, which can be inferred from a vector's direction, is a measure of its steepness or incline. It is a key concept when dealing with linear equations and is mentioned in the video as something that can be determined once a vector is represented in a certain form, such as standard form or slope-intercept form.
💡Intercepts
Intercepts refer to the points where a line or vector crosses the axes on a coordinate system. The video mentions that knowing the intercepts can be useful for solving various mathematical problems, particularly when dealing with linear equations.
💡Standard Form
Standard form is a way of writing a linear equation, typically in the form Ax + By = C, where A, B, and C are constants. The video discusses the importance of standard form in organizing and solving mathematical problems, and it draws a parallel to the component form of a vector.
💡Slope-Intercept Form
Slope-intercept form is a way of writing a linear equation in the form y = mx + b, where m is the slope and b is the y-intercept. The video uses this form as an example of how different forms can help in solving mathematical problems and understanding the properties of vectors.
💡Vertex Form
Vertex form is another way to represent a quadratic equation, typically written as y = a(x - h)² + k, where (h, k) is the vertex of the parabola. The video briefly mentions vertex form as one of the various forms used in mathematical problem-solving, suggesting its relevance to understanding vectors and their properties.
Highlights

Introduction to the concept of a vector on a plane without axes.

Placement of a vector on the Cartesian coordinate system for analysis.

Focus on the x and y coordinates of a vector, referred to as P and Q.

Differentiation between the points P1, P2 and Q1, Q2 on a vector.

Importance of standard forms in equations for problem-solving.

Linking the concept of vector representation to standard form equations.

Explanation of the vector's initial and terminal points.

Derivation of the component form of a vector, V, as Q1 - P1, Q2 - P2.

Example calculation of the component form using points (4, 2) and (10, 9).

Result of the example showing the component form as 6, 7.

Purpose of component form: simplifying vector representation with the initial point at origin (0, 0).

Visual demonstration of how component form affects the appearance of a vector's slope and magnitude.

Advantage of using component form for standardized vector operations.

Assurance that understanding component form is fundamental and not overly complex.

Reiteration of the process for finding the component form of a vector.

Anticipation of increasing complexity in vector analysis.

Confirmation that despite potential complexity, the foundational concepts remain manageable.

Transcripts

Browse More Related Video

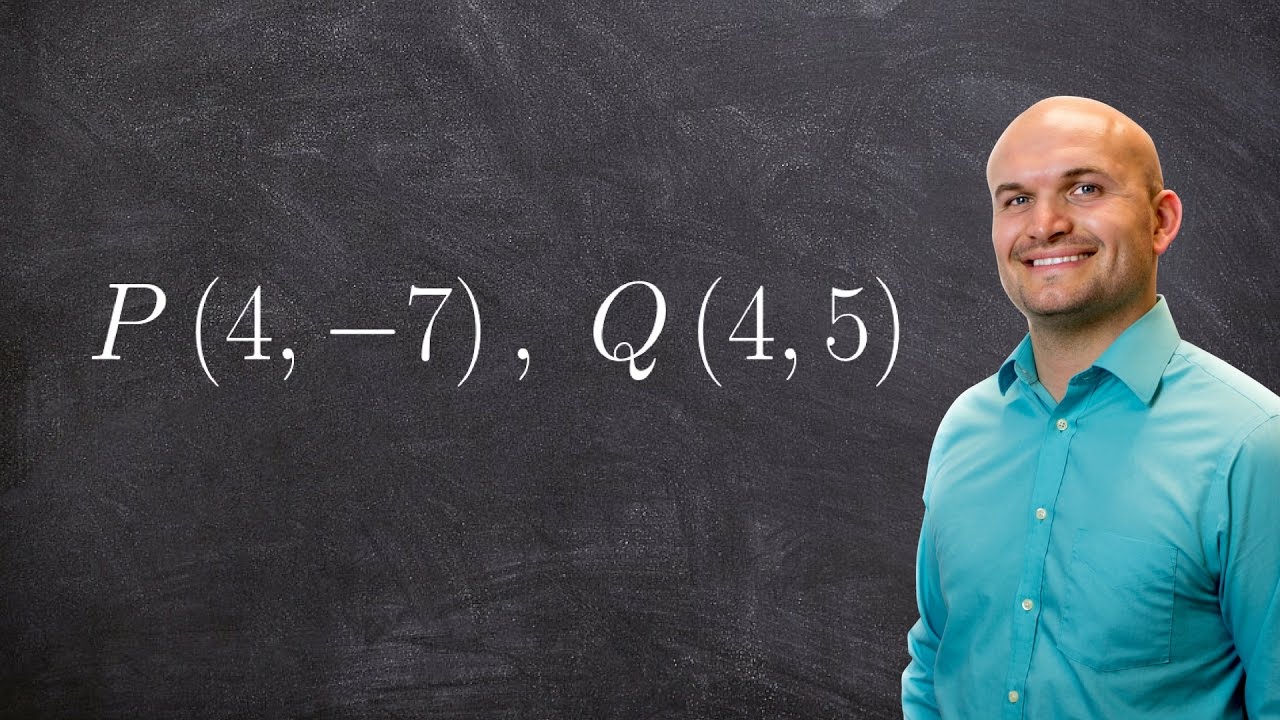
How to find the component form and magnitude of a vector

Unit Vectors | Physics with Professor Matt Anderson | M3-06

Engineering Mechanics: Statics Lecture 4 | Cartesian Vectors in 3D

Force Vectors Along a Line | Mechanics Statics | (Learn to solve any question)

Ch. 9.1 Vectors in Two Dimensions

The Vector Equation of Lines | Multivariable Calculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Vector AnalysisComponent FormCartesian SystemMathematicsEducational ContentSlope CalculationMagnitudeVector RepresentationStandard FormMath TutorialGeometry