Force Vectors Along a Line | Mechanics Statics | (Learn to solve any question)
TLDRThis script offers a step-by-step guide to expressing forces directed along a line in Cartesian form. It begins with identifying position vectors and their magnitudes, then moves on to calculating unit vectors and multiplying them by the force to achieve the Cartesian representation. The process is illustrated with examples, including finding resultant forces and coordinate direction angles using trigonometric functions. The script concludes with a problem-solving approach for locating points given forces in Cartesian form, aiming to assist students in understanding vector addition and force calculations.
Takeaways
- 📚 To express a force in Cartesian form, one must follow a series of steps involving position vectors and unit vectors.
- 📍 A position vector, denoted by 'r', is a vector from one point to another and can be found by subtracting the coordinates of the starting point from the ending point.
- 🔍 The magnitude of a position vector is calculated by squaring each component, summing them, and then taking the square root.
- 🧭 Unit vectors are derived by dividing each component of the position vector by its magnitude.
- 🔄 To find the resultant force, express each individual force in Cartesian form and then add the corresponding components together.
- 📈 The process involves writing down the locations of all points of interest, calculating position vectors, finding their magnitudes, and determining unit vectors.
- 📝 When given a force along a line, the position vector is the difference between the coordinates of the points where the force starts and ends.
- 🔢 The magnitude of the position vector represents the distance between two points, which is also the length of the rope in the given examples.
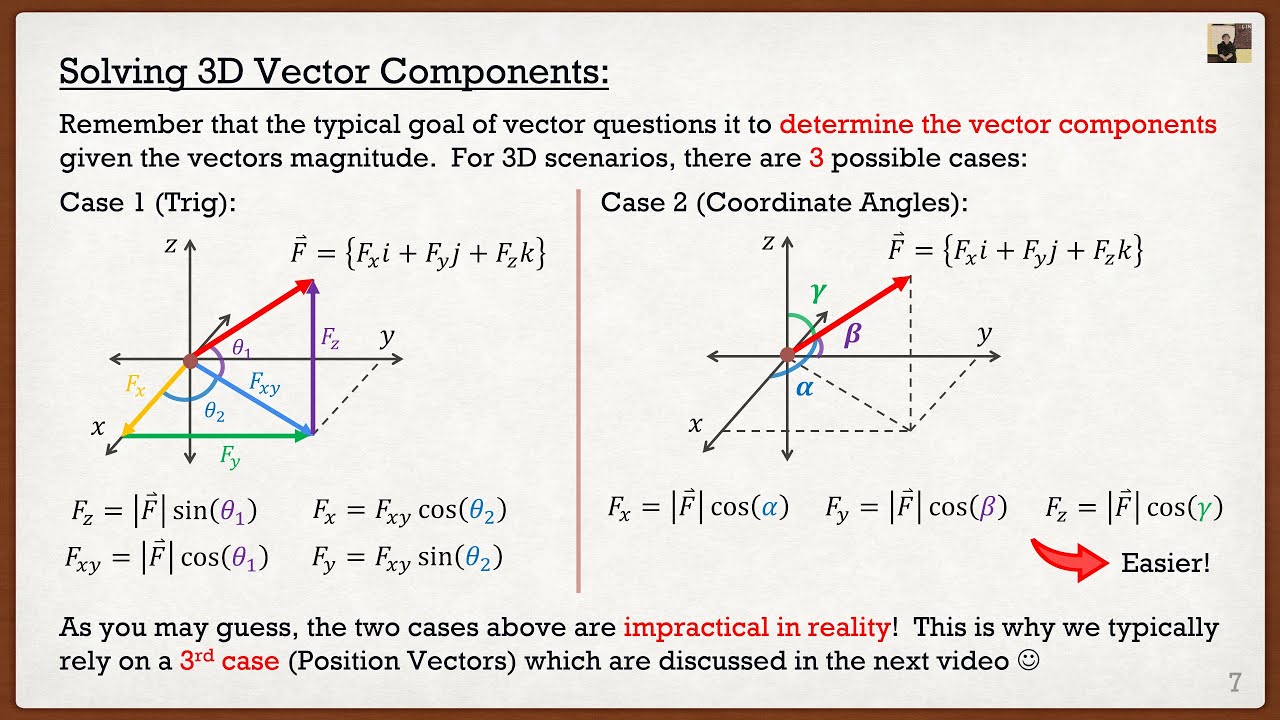
- 📐 Coordinate direction angles can be found using inverse cosine functions applied to the Cartesian components of the force.
- 🔗 When forces are given in Cartesian form, the location of a point can be determined by equating the components of the given force to the unit vector multiplied by an unknown magnitude.
- 🤝 The script encourages sharing the information with friends and classmates who might also find it useful for their studies.
Q & A
What is a position vector and how is it represented?
-A position vector is a vector directed from one point to another, represented by the letter 'r'.
How do you find the magnitude of a position vector?
-To find the magnitude of a position vector, take each component, square it, sum these squares, and then take the square root of the total.
What is a unit vector and how is it calculated?
-A unit vector is a vector that has a magnitude of 1. It is calculated by dividing each component of the position vector by its magnitude.
How do you express a force in Cartesian form?
-To express a force in Cartesian form, multiply the force magnitude by the unit vector. This involves multiplying each component of the unit vector by the magnitude of the force.
What is the first step in finding a force in Cartesian form?
-The first step is to write down the locations of all the points of interest.
How do you find the position vector for a force between two points?
-Subtract the position of the starting point from the position of the ending point. This is done by subtracting each component of the starting point from the corresponding component of the ending point.
What is the process to find the resultant force from multiple forces in Cartesian form?
-Add the corresponding components of each force vector together: i components to i components, j components to j components, and k components to k components.
How do you calculate the magnitude of a resultant force?
-Calculate the magnitude of the resultant force by squaring each component, summing these squares, and taking the square root of the total.
How can you find the coordinate direction angles of a force vector?
-The coordinate direction angles can be found using the inverse cosine of the components of the unit vector.
What should you do if you are given a force in Cartesian form and need to find the location of a point?
-Write down the positions using variables for the unknowns, create a position vector, and use the given magnitude and direction to solve for the unknown coordinates by equating the components.
Outlines
🔗 Transforming Forces into Cartesian Form
This paragraph introduces the concept of expressing forces in Cartesian form, particularly when given forces from one point to another, such as a force along a rope. It outlines the necessary steps to achieve this transformation, emphasizing the importance of understanding position vectors. A position vector, denoted by 'r', represents the direction from one point to another. To convert this into Cartesian form, one needs to calculate the magnitude of the position vector by squaring its components and taking the square root. By dividing each component by the magnitude, a unit vector is obtained. The paragraph also sets the stage for practical examples, illustrating the process with points A, B, and C, and demonstrating how to write position vectors, calculate their magnitudes, and ultimately express forces in Cartesian form.
🧮 Applying Cartesian Force Calculations
This paragraph continues with practical examples of converting forces into Cartesian form. It walks through a problem where forces are directed along lines, specifically from point A to points B and C. The steps involve identifying the locations of points A, B, and C, writing down the position vectors, and calculating their magnitudes. The magnitudes represent the distances between the points, or the lengths of the ropes. By finding the unit vectors and multiplying by the respective forces, the forces in Cartesian form are obtained. The paragraph concludes by showing how to add these forces together to get the resultant force and calculate its magnitude, followed by determining the coordinate direction angles using inverse cosine.
📐 Finding Point Locations from Cartesian Forces
This paragraph addresses a scenario where a force is already given in Cartesian form, and the task is to find the location of point B. It begins by writing down the locations of points A and B, using x, y, and z to represent unknown values. A position vector from A to B is written and simplified. Given the length of the rope (magnitude), the unit vector is found by dividing each term in the position vector by the magnitude. With the Cartesian form of the force provided, the magnitude of this force is calculated. The solution involves equating the components of the Cartesian force with the unit vector components, solving for the unknowns. The paragraph concludes by summarizing the types of problems related to forces directed along a line and encouraging viewers to share the video if they found it helpful.
Mindmap
Keywords
💡Force
💡Cartesian Form
💡Position Vector
💡Magnitude
💡Unit Vector
💡Resultant Force
💡Coordinate Direction Angles
💡Inversion of Cosine
💡Location
💡Normalization
Highlights
Expressing force in Cartesian form requires a set of steps involving position vectors and unit vectors.
A position vector, represented by 'r', is a vector from one point to another and its magnitude is found by squaring and rooting the components.
Unit vectors are derived by dividing each component of the position vector by its magnitude.
Cartesian form of force is found by multiplying the unit vector by the force magnitude.
Example given to demonstrate expressing force in Cartesian form using points A, B, and C with respective positions.
Position vectors are calculated by subtracting the starting point's coordinates from the ending point's.
The magnitude of the position vector represents the distance between two points, such as the length of a rope.
Coordinate direction angles can be found using inverse cosine functions applied to the Cartesian components of force.
A detailed explanation of the addition of Cartesian vectors is available in a previous video.
Forces in ropes can be expressed in Cartesian form by calculating position vectors for each rope segment.
The process of finding the resultant force involves adding the Cartesian components of individual forces.
When a force is given in Cartesian form, the location of a point can be found by equating and solving the components.
The magnitude of a given force in Cartesian form can be used to find the unit vector and subsequently the point's location.
The video provides a comprehensive guide to handling forces directed along a line in a Cartesian coordinate system.
The video encourages sharing the knowledge with friends and classmates for mutual benefit.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: