How To Use The Parallelogram Method To Find The Resultant Vector

The Organic Chemistry Tutor
21 Aug 202205:11
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script introduces the parallelogram method for calculating the magnitude of the resultant vector from two given force vectors, f1 and f2. It explains the process of constructing a parallelogram with vectors f1 and f2, and then using the law of cosines to find the magnitude of the resultant vector (fr). The example provided uses specific values for f1 and f2, and demonstrates the calculation step by step, leading to a final magnitude of approximately 147.3 Newtons for the resultant force vector.

Takeaways
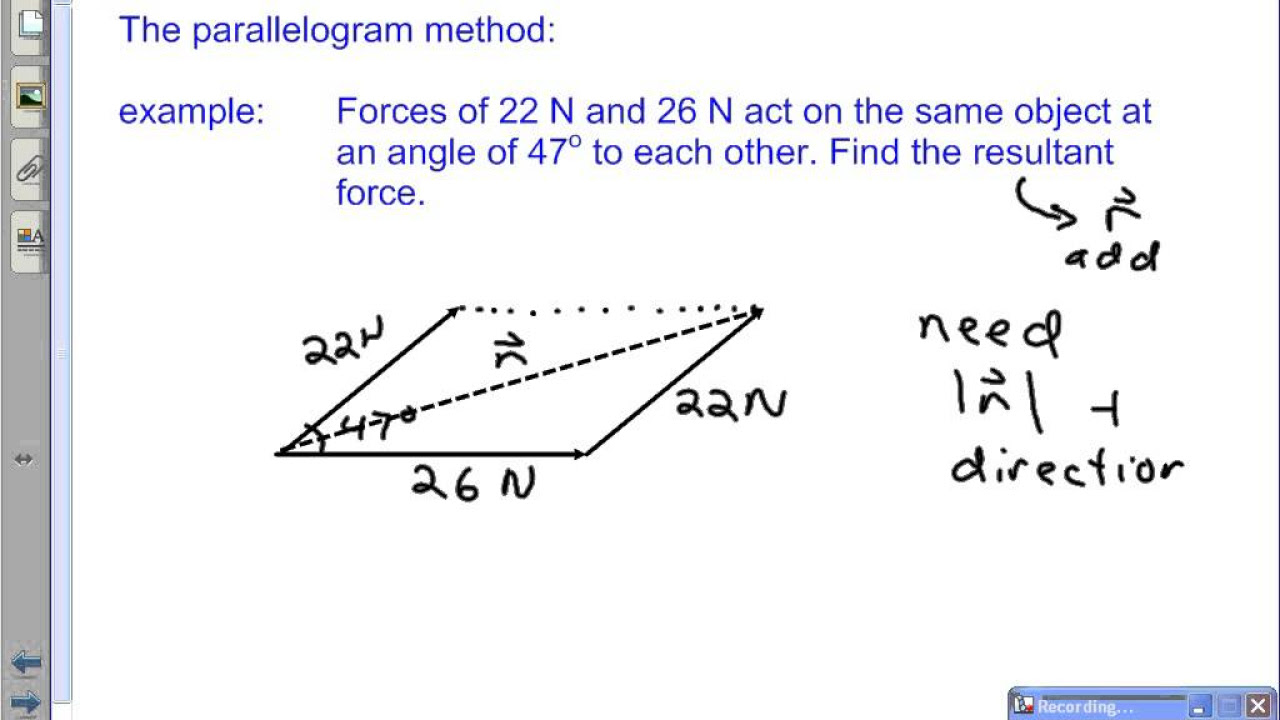
  • ๐Ÿ“ The lesson discusses the use of the parallelogram method to find the magnitude of the resultant vector.
  • ๐Ÿ” The resultant vector (FR) lies somewhere in the middle of two given vectors (F1 and F2).
  • ๐ŸŽจ To apply the method, draw parallel vectors for F1 and F2, forming a parallelogram.
  • ๐Ÿ”„ The intersection of the first two vectors is connected to the intersection of the last two vectors, yielding the resultant vector.
  • ๐Ÿ”ข Adjacent angles in the parallelogram are supplementary, meaning they add up to 180 degrees.
  • ๐Ÿ“ The law of cosines is used to calculate the magnitude of the resultant vector: cยฒ = aยฒ + bยฒ - 2ab*cos(c), where a and b are the magnitudes of F1 and F2, and c is the angle between them.
  • ๐Ÿ“Š Given values in the example are F1 = 80, F2 = 90, and angle between them (c) = 120 degrees.
  • ๐Ÿงฎ The calculation involves squaring the magnitudes of F1 and F2, finding the product of F1 and F2, and then applying the cosine of the angle.
  • ๐Ÿ”ข The resultant vector squared (FRยฒ) is calculated as 20,700, and the square root gives the magnitude of the resultant vector.
  • ๐Ÿ“ˆ The magnitude of the resultant force vector (FR) is approximately 147.3 Newtons.
  • ๐Ÿ“š The lesson provides a practical approach to understanding vector addition and the calculation of resultant forces in physics.
Q & A

  • What is the main topic of the lesson?

    -The main topic of the lesson is how to use the parallelogram method to find the magnitude of the resultant vector of two given vectors.

  • What are the two vectors being discussed in the lesson?

    -The two vectors being discussed are force vectors f1 and f2.

  • How is the resultant vector, fr, determined using the parallelogram method?

    -The resultant vector fr is determined by drawing parallel vectors to f1 and f2, forming a parallelogram, and then drawing an arrow from the intersection of the first two vectors to the intersection of the last two vectors.

  • What is the significance of the angle between the adjacent sides of the parallelogram?

    -The angle between the adjacent sides of the parallelogram is significant because it is supplementary to 180 degrees, which is necessary for applying the law of cosines to find the magnitude of the resultant vector.

  • What is the law of cosines?

    -The law of cosines states that in a triangle, the square of one side length (c) is equal to the sum of the squares of the other two side lengths (a and b) minus twice the product of those two side lengths multiplied by the cosine of the included angle (C).

  • How are the side lengths of the parallelogram related to the magnitudes of vectors f1 and f2?

    -In the parallelogram, the side lengths correspond to the magnitudes of vectors f1 and f2, with f1 being 80 and f2 being 90.

  • What is the value of angle c in the context of the lesson?

    -In the context of the lesson, angle c is the angle between the resultant vector fr and one of the sides of the parallelogram, which is 120 degrees.

  • How is the law of sines mentioned in the lesson?

    -The law of sines is mentioned as a potential tool to find other angles in the triangle formed by the vectors and the resultant vector, although the focus of the lesson is on finding the magnitude of the resultant vector.

  • What is the final calculated magnitude of the resultant vector fr?

    -The final calculated magnitude of the resultant vector fr is approximately 147.3 Newtons.

  • How does the parallelogram method help in vector analysis?

    -The parallelogram method provides a geometric approach to vector addition, allowing for the visualization and calculation of the resultant vector's magnitude by forming a parallelogram with the given vectors and applying the law of cosines.

  • What is the mathematical process to find the magnitude of the resultant vector using the parallelogram method?

    -The mathematical process involves applying the law of cosines, where the square of the resultant vector (c) is calculated as the sum of the squares of the magnitudes of vectors f1 (a) and f2 (b) minus twice the product of those magnitudes multiplied by the cosine of the angle between them (cosine of 120 degrees).

Outlines
00:00
๐Ÿ“ Understanding the Parallelogram Method for Vector Magnitude

This paragraph introduces the concept of using the parallelogram method to calculate the magnitude of the resultant vector from two given vectors, f1 and f2. It explains the process of constructing a parallelogram with the vectors and how to find the resultant vector by drawing an arrow from the intersection of the first two vectors to the intersection of the last two vectors. The paragraph also delves into the geometric principle that adjacent angles in a parallelogram are supplementary, adding up to 180 degrees. It further discusses the application of the law of cosines in a triangle to find the magnitude of the resultant vector, providing a step-by-step calculation using the given vector lengths and the included angle. The final result is the magnitude of the resultant vector, approximately 147.3 Newtons.

05:03
๐Ÿš€ Applying the Parallelogram Method in Force Analysis

The second paragraph serves as a brief conclusion to the explanation, summarizing the process of finding the magnitude of a force vector using the parallelogram method. It reinforces the idea that this method is an effective way to analyze and calculate the resultant of two vectors in a force context.

Mindmap
Keywords
๐Ÿ’กParallelogram Method
The Parallelogram Method is a vector addition technique used to find the resultant vector when two vectors are given. In the context of the video, it is the primary tool to calculate the magnitude of the resultant force vector, denoted as fr, by constructing a parallelogram with vectors f1 and f2 as adjacent sides. This method is visually demonstrated by drawing parallel vectors to form the parallelogram, and the resultant vector is found by drawing an arrow from the tail of the first vector to the head of the last vector.
๐Ÿ’กResultant Vector
A resultant vector is the single vector that represents the combined effect of two or more vectors. In the video, the resultant vector, fr, is the sum of the two force vectors, f1 and f2. The magnitude of the resultant vector is the focus of the lesson, as it provides the overall effect of the two individual forces acting together.
๐Ÿ’กForce Vectors
Force vectors, denoted as f1 and f2 in the script, are vectors that represent physical forces with both magnitude and direction. They are the inputs to the parallelogram method for finding the resultant vector. These vectors are used to illustrate the concept of vector addition and how their combined effect can be represented by a single resultant vector.
๐Ÿ’กLaw of Cosines
The Law of Cosines is a mathematical formula used in trigonometry to find a side length of a triangle when the lengths of the other two sides and the cosine of the included angle are known. In the video, the law of cosines is applied to the parallelogram, which is treated as a triangle with the resultant vector as the third side, to find the magnitude of the resultant vector.
๐Ÿ’กSupplementary Angles
Supplementary angles are two angles whose measures add up to 180 degrees. In the video, the term is used to describe the relationship between adjacent angles in the parallelogram, which are supplementary because they add up to 180 degrees. This property is crucial for applying the law of cosines to find the resultant vector.
๐Ÿ’กVector Magnitude
The magnitude of a vector is its length or size, which can be found by calculating the square root of the sum of the squares of its components. In the video, the magnitude of the resultant vector (fr) is the main objective, representing the overall strength of the combined forces.
๐Ÿ’กTriangle
A triangle in this context is a geometric figure used to illustrate the relationship between the vectors and the resultant vector in the parallelogram method. The sides of the triangle correspond to the magnitudes of the vectors, and the angles correspond to the directions of the vectors.
๐Ÿ’กTrigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It is used in the video to apply the law of cosines to find the magnitude of the resultant vector in the parallelogram method.
๐Ÿ’กCalculation
Calculation refers to the process of performing mathematical operations to find a solution or an answer. In the video, calculations are performed to determine the magnitude of the resultant vector using the parallelogram method and the law of cosines.
๐Ÿ’กNewtons
Newtons are the unit of force in the International System of Units (SI). In the video, the magnitude of the resultant vector is given in Newtons, which indicates the combined force exerted by the two original force vectors.
๐Ÿ’กVector Addition
Vector addition is the process of combining two or more vectors to find a single vector that represents their combined effect. In the video, vector addition is demonstrated through the parallelogram method, where the resultant vector is the sum of the force vectors f1 and f2.
Highlights

Introduction to the parallelogram method for finding the magnitude of the resultant vector.

Explanation of resultant vector positioning within the parallelogram formed by vectors f1 and f2.

Step-by-step illustration of constructing a parallelogram with vectors f1 and f2.

Use of supplementary angles in parallelograms, specifically adjacent angles adding up to 180 degrees.

Application of the law of cosines in vector analysis for calculating the magnitude of the resultant vector.

Detailed breakdown of the law of cosines formula in the context of the given vectors f1 and f2.

Assignment of values to the vectors f1 and f2 for the practical example.

Substitution of values into the resultant vector equation using the law of cosines.

Calculation of the resultant vector squared (f_r^2) using the provided numerical values.

Inclusion of the cosine value for the 120-degree angle in the calculation.

Final computation leading to the magnitude of the resultant vector in newtons.

Explanation of how the magnitude of the resultant vector can be used to find other angles using the law of sines.

Emphasis on focusing solely on the magnitude of the resultant vector (f_r) in this lesson.

Demonstration of the practical application of the parallelogram method in vector analysis.

Conclusion summarizing the process of finding the magnitude of the resultant force vector using the parallelogram method.

Transcripts

Browse More Related Video

Lesson 6 - Finding The Resultant Of Two Forces, Part 2 (Engineering Mechanics Statics)

Calculating the Resultant force Using Parallelogram Law, แˆˆแŠขแ‰ตแ‹ฎแŒตแ‹ซแ‹แ‹ซแŠ•

Lesson 5 - Finding The Resultant Of Two Forces, Part 1 (Engineering Mechanics Statics)

1-2 C Vector Addition - 2 (Parallelogram Method)

AP Physics B Kinematics Presentation General Problems #08

4 Resultant force of two vectors at different angles

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics TutorialVector MagnitudeParallelogram LawForce AnalysisMathematical CalculationEducational ContentPhysics ConceptsVector AnalysisLaw of CosinesVector Mathematics