Torque Example #3: Leaning Ladder Problem
TLDRThe video script presents a detailed explanation of the 'Leaning Ladder' problem, a classic torque example. The ladder, weighing 400 newtons and measuring 5 meters in length, leans against a frictionless wall and has friction on the floor. The objective is to determine the forces exerted by the wall and floor on the ladder. The problem is approached by balancing horizontal and vertical forces, and then applying the principle of zero net torque around the pivot point where the ladder contacts the floor. By calculating the torques created by the ladder's weight and the wall's normal force, the video demonstrates how to find the force exerted by the wall, which is identified as 150 newtons. This force also corresponds to the static frictional force preventing the ladder from slipping. The summary concludes by highlighting the utility of the line of action approach in solving such problems and encourages further practice with this method.
Takeaways
- 📐 The Leaning Ladder problem is a famous torque example used to illustrate the principles of static friction and normal forces.
- 🧮 The ladder has a weight of 400 Newtons and is 5 meters long, creating a 53-degree angle against a frictionless wall.
- 📏 The ladder's length is divided into two components: 4 meters against the wall and 3 meters on the floor.
- 💥 There's no friction at the point where the ladder contacts the wall, but there is friction on the floor.
- 🔄 The goal is to find the force that the wall exerts on the floor, known as the normal force, and the total force exerted by the floor on the ladder.
- ⚖️ Two forces are exerted by the floor on the ladder: the normal force (F_n floor) and the static frictional force that prevents the ladder from slipping.
- ➡️ The wall only exerts a normal force on the ladder since there is no friction.
- ⚙️ The problem-solving approach involves setting up equations for the horizontal forces (ΣFx = 0), vertical forces (ΣFy = 0), and torque (Σtorque = 0).
- 🎛️ The normal force from the floor (F_n floor) is equal to the weight of the ladder, which is 400 Newtons.
- 🔄 The horizontal forces are balanced, meaning the force exerted by the wall equals the static friction force.
- 📐 The torque from the weight of the ladder is calculated using the moment arm, which simplifies the calculation process.
- 🔩 The final solution involves calculating the force of the wall and the total force exerted by the floor on the ladder, using the line of action and moment arm approach.
Q & A
What is the 'Leaning Ladder Problem' that the speaker is referring to?
-The 'Leaning Ladder Problem' is a torque problem involving a ladder leaning against a frictionless wall with friction on the floor. The goal is to determine the force that the wall exerts on the floor, which is the normal force, and the total force exerted by the floor on the ladder.
What are the two forces exerted by the floor on the ladder?
-The two forces exerted by the floor on the ladder are the normal force, which is perpendicular to the surface, and the frictional force, which is parallel to the surface and prevents the ladder from slipping.
What is the length of the ladder in the problem?
-The ladder is 5 meters long.
What is the weight of the ladder in newtons?
-The weight of the ladder is 400 newtons.
What is the approach to solving the problem using the equations of motion?
-The approach involves setting up equations based on the equilibrium of forces (ΣFx = 0 and ΣFy = 0) and the equilibrium of torques (Στ = 0), where the torque is calculated about the pivot point where the ladder contacts the floor.
How is the weight of the ladder related to the normal force from the floor?
-The weight of the ladder is equal to the normal force from the floor, which is 400 newtons, as there is no other vertical force acting on the ladder.
What is the concept of the moment arm and how is it used in this problem?
-The moment arm is the distance from the pivot point to the line of action of a force, perpendicular to the force. In this problem, it is used to calculate the torque caused by the weight of the ladder and the force from the wall, which helps in balancing the torques to solve for the unknown forces.
What is the clockwise torque caused by the weight of the ladder?
-The clockwise torque caused by the weight of the ladder is the product of the weight (400 newtons) and the moment arm (1.5 meters), which equals 600 newton meters.
How is the force of the wall calculated using torque?
-The force of the wall is calculated by balancing the counterclockwise torque it provides with the clockwise torque from the weight of the ladder. The counterclockwise torque is the product of the unknown wall force and the moment arm (4 meters), which equals 600 newton meters, thus the force of the wall is 150 newtons.
What is the total force exerted by the floor on the ladder in the horizontal direction?
-The total force exerted by the floor on the ladder in the horizontal direction is the sum of the static friction force (150 newtons) and the normal force from the wall (400 newtons), assuming the normal force has a horizontal component due to the angle of the ladder.
What is the speaker's preferred method for calculating torques in this problem?
-The speaker's preferred method for calculating torques in this problem is using the moment arm and line of action, which simplifies the calculations and provides a clear visualization of the forces involved.
Why is it important to choose the right axis for torque calculations?
-Choosing the right axis for torque calculations is important because forces that act directly at the axis of rotation provide no torque. This allows for simplification of the problem and makes it easier to calculate the torques exerted by the different forces acting on the ladder.
Outlines
🔍 Introduction to the Leaning Ladder Problem
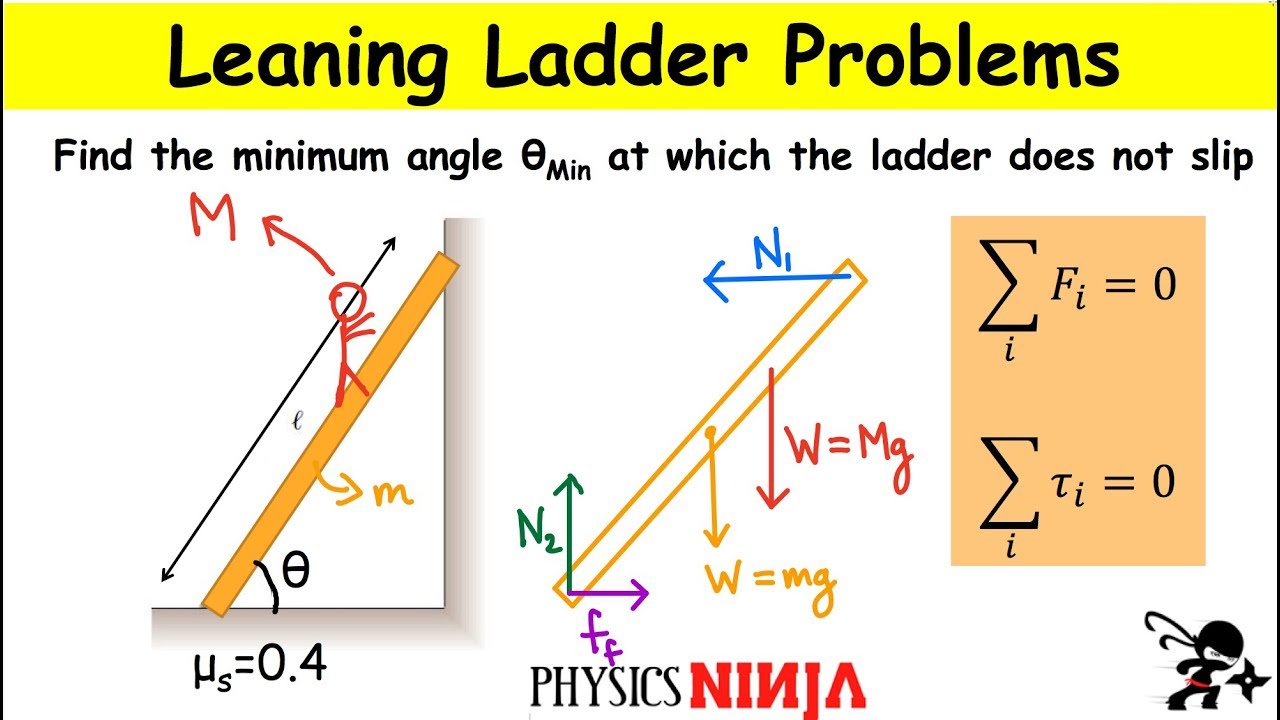
The first paragraph introduces a famous physics problem known as the leaning ladder problem. The problem involves a ladder that is 5 meters long and weighs 400 newtons, leaning against a frictionless wall at a 53-degree angle. The ladder also makes contact with the floor, which has friction. The goal is to determine the force exerted by the wall on the floor (normal force) and the total force exerted by the floor on the ladder. The paragraph outlines the forces involved, including the normal force from the floor (f_n floor), the static frictional force that prevents the ladder from slipping, and the normal force from the wall (f_w). The problem is approached by setting up equations based on force balance (ΣFx = 0, ΣFy = 0) and torque balance (Σtorque = 0), with the weight of the ladder acting at its center of mass and the normal forces from the wall and floor being the primary forces of interest.
📐 Solving the Leaning Ladder Problem Using Torque
The second paragraph delves into solving the leaning ladder problem by focusing on the concept of torque. The torque equation Σtorque = 0 is used to balance the clockwise and counterclockwise torques acting on the ladder. The axis of rotation is chosen at the point where the ladder contacts the floor, which simplifies the calculation by eliminating the forces acting directly at the axis from the torque equation. The weight of the ladder provides a clockwise torque, while the force from the wall provides a counterclockwise torque. Using the moment arm concept, the torque from the weight of the ladder is calculated as the force (400 newtons) times the moment arm (1.5 meters), resulting in a clockwise torque of 600 newton meters. The counterclockwise torque is calculated by considering the force from the wall and its moment arm, which is found to be 4 meters. By setting the clockwise torque equal to the counterclockwise torque, the force of the wall is determined to be 150 newtons. Consequently, the static frictional force is also 150 newtons. The final answer includes the force of the wall (150 newtons), the total force of the floor in the x-direction (static friction of 150 newtons plus the normal force from the wall of 400 newtons), and the direction of these forces.
Mindmap
Keywords
💡Torque
💡Normal Force
💡Frictional Force
💡Static Friction
💡Moment Arm
💡Line of Action
💡Equilibrium
💡Center of Mass
💡Frictionless Wall
💡Newton
💡Degrees of Freedom
Highlights
Introduction to the famous 'leaning ladder' problem, a classic example in torque analysis.
The ladder is 5 meters long and weighs 400 newtons, leaning against a frictionless wall.
Friction is present on the floor, not on the wall, which affects the forces acting on the ladder.
The goal is to determine the normal force exerted by the wall and the total force exerted by the floor on the ladder.
Identification of two forces exerted by the floor: the normal force (F_n floor) and the static frictional force.
Explanation of the difference between normal and frictional forces in contact force scenarios.
Application of the principle of equilibrium: ΣF_x = 0 and ΣF_y = 0, to balance horizontal and vertical forces.
Determination that the normal force from the floor (F_n floor) equals the weight of the ladder, which is 400 newtons.
Use of the torque equation (Σ torque = 0) to solve for the unknown forces, with the pivot point at the floor-ladder contact.
Simplification of the torque equation by placing the axis of rotation at the point of contact between the ladder and the floor.
Calculation of the torque from the weight of the ladder using the moment arm concept.
Moment arm for the weight of the ladder is found to be 1.5 meters, resulting in a clockwise torque of 600 newton meters.
Calculation of the counterclockwise torque from the wall's force, using a moment arm of 4 meters.
Balancing the torques to find that the force of the wall is 150 newtons, which also equals the frictional force.
Final answer includes the force of the wall (150 newtons) and the total force of the floor on the ladder (static friction + normal force from the wall).
Emphasis on the usefulness of the line of action and moment arm approach in simplifying torque calculations.
Recommendation to practice using the line of action approach for better understanding and application in similar problems.
Transcripts
Browse More Related Video

Ladder Example for Static Equilibrium

The Leaning Ladder Problem | Physics with Professor Matt Anderson | M12-22
Physics 15 Torque (21 of 25) More Examples: 3 T=? of Cable of Step Ladder

Physics 15 Torque (3 of 27) Tension=? in the Cable
Leaning Ladder Equilibrium Problem: Find Minimum Angle
Physics 15 Torque (11 of 27) Example 1: Forces=?
5.0 / 5 (0 votes)
Thanks for rating: