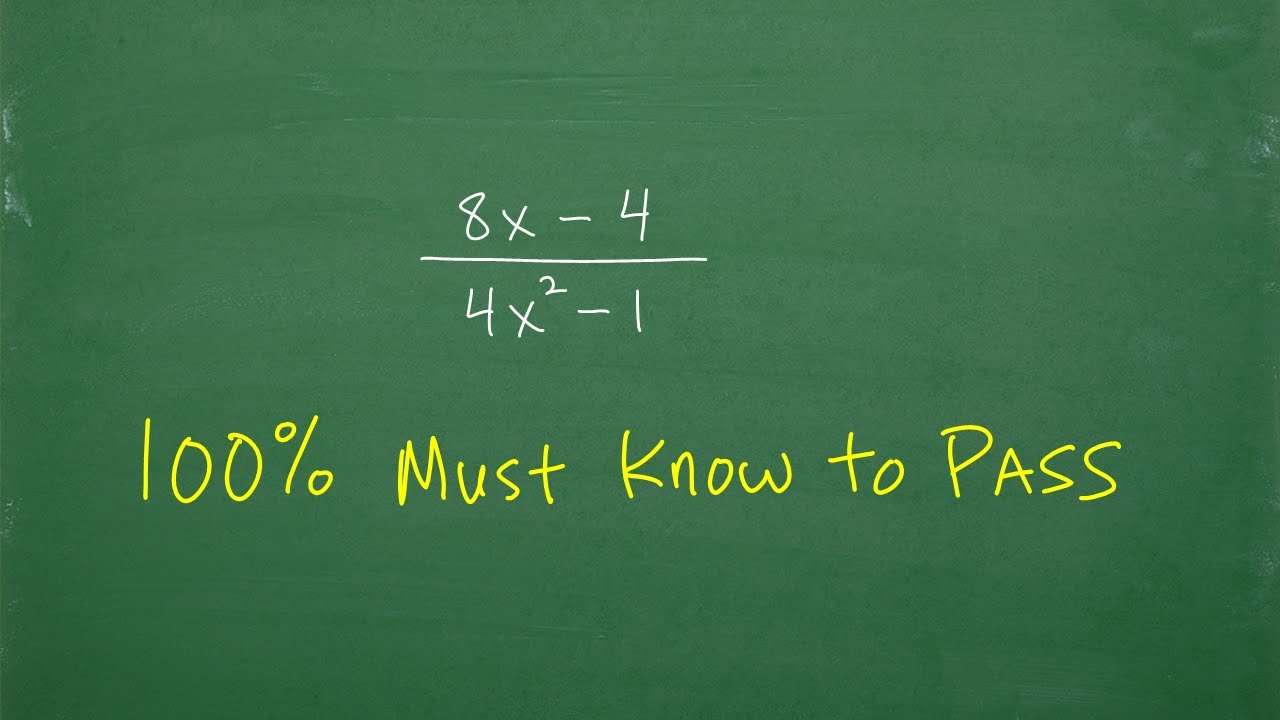What Makes People Engage With Math | Grant Sanderson | TEDxBerkeley
TLDRThe speaker explores what makes people engage with math, using insights from his YouTube channel where he teaches complex mathematical concepts. He emphasizes the importance of visualization and storytelling, noting that while relevance is key, it's not the only factor. He argues that the emotional appeal of math, much like fiction, can captivate an audience. The speaker shares examples from his most engaging videos, such as Fourier transforms and neural networks, and discusses the surprising popularity of seemingly impractical problems. He concludes that the intertwining of usefulness and story is what truly engages people with math, highlighting the unexpected connections and applications that can arise from seemingly abstract mathematical pursuits.
Takeaways
- 📚 **Engagement through Relevance**: Connecting math to real-world applications helps people see its value and relevance, which can increase engagement.
- 🎓 **Visualization and Animation**: Using visual aids and animations can make complex mathematical concepts more accessible and engaging, especially for those without a deep technical background.
- 🤔 **Addressing the 'When Will I Use It?' Question**: Presenting math in a way that answers the common question of practical application can help students feel that learning math is worthwhile.
- 🏋️♂️ **Math as a 'Gym for the Mind'**: Just like going to the gym, doing math can be seen as an effort that yields a sense of accomplishment, power, and even pride.
- 🧩 **The Power of Storytelling**: Incorporating elements of story, emotion, and character into math can make it more engaging, similar to how fiction captivates audiences.
- 🎭 **Appealing to Emotions**: Math can be engaging when it appeals to emotions, curiosity, and the desire to solve a mystery or see a resolution, much like a good novel.
- 🔍 **Unexpected Connections**: Even seemingly 'useless' math can have unexpected practical applications, as demonstrated by the evolution of theories in physics and cryptography.
- 🌐 **The Internet as a Content Proving Ground**: Online platforms like YouTube provide a unique stress test for content engagement, where viewers have countless alternatives just a click away.
- 📈 **The Role of Challenge and Mystery**: Presenting math problems that are challenging and mysterious, like a detective story, can draw in an audience and encourage them to follow along.
- 🎓 **Humanizing Math**: Channels like Numberphile humanize math by showcasing the personalities and stories of mathematicians, making the subject more relatable.
- 📉 **The Unexpected Utility of Pure Math**: Even math that is initially considered pure and without application can eventually prove to be incredibly useful in unforeseen ways.
Q & A
What is the main challenge in engaging students with math?
-The main challenge is making math relevant and interesting to students, showing them how it can be applied in real-world contexts, and overcoming the intimidation that can come with complex mathematical concepts.
Why is the Fourier transform considered a 'problem-solving superpower'?
-The Fourier transform is a 'problem-solving superpower' because it allows us to break down complex functions into pure frequencies, which is applicable in various fields such as sound engineering, electrical engineering, quantum mechanics, and physics.
What is the role of visualization in teaching math?
-Visualization, including animations, plays a significant role in teaching math by providing a more accessible and intuitive understanding of complex concepts before introducing formal mathematical notations.
How does the speaker use the example of neural networks to engage viewers?
-The speaker uses the example of neural networks to engage viewers by showing the highly visualizable aspects of the subject, such as how training examples are used to recognize patterns, before diving into the formalisms of matrix operations and nonlinearities.
What is the importance of answering the question 'When am I ever going to use this?' in math education?
-Answering the question 'When am I ever going to use this?' is crucial in math education because it helps students see the relevance of what they are learning, making the subject less abstract and more connected to their lives.
Why does the speaker believe that 'story' is an important component in engaging people with math?
-The speaker believes that 'story' is an important component in engaging people with math because it appeals to emotions, creates a sense of wonder, and establishes a narrative that draws people in, similar to how fiction does.
What is the significance of the block collision problem discussed in the script?
-The block collision problem is significant because it presents a seemingly simple scenario with a surprisingly complex outcome that is related to the digits of pi. This unexpected connection makes the problem intriguing and encourages deeper exploration into the mathematics involved.
How does the sphere problem from the Putnam test engage viewers?
-The sphere problem engages viewers by positioning itself as one of the hardest problems on a notoriously difficult test. This creates a sense of challenge and intrigue, making viewers feel as if they are part of an exclusive group capable of understanding complex mathematical concepts.
What is the role of emotion and character in making math more engaging?
-Emotion and character play a role in making math more engaging by humanizing the subject, making it relatable, and providing a narrative that viewers can connect with on a personal level.
Why does the speaker argue that even seemingly 'useless' math can have real-world applications?
-The speaker argues that even seemingly 'useless' math can have real-world applications because mathematical concepts often reveal unexpected connections and can be applied in ways that were not initially apparent, as demonstrated by the examples of number theory and relativity.
How does the speaker suggest we can make math more engaging for students?
-The speaker suggests that we can make math more engaging for students by combining the usefulness of math with a compelling narrative or story, leveraging emotions, and showing the beauty and wonder of mathematical concepts.
What is the role of YouTube in teaching and engaging people with math?
-YouTube plays a role in teaching and engaging people with math by providing a platform for educators to present complex concepts in a visual and accessible way, using storytelling and relatable examples to maintain viewer interest and encourage learning.
Outlines
📚 Engaging with Math through YouTube
The speaker discusses the challenge of engaging students with math, especially in the context of a platform like YouTube where viewers have countless entertainment options at their fingertips. They share their experience of creating math content on YouTube that not only educates but also retains the interest of the audience. The speaker emphasizes the importance of making math relatable and visually appealing, using examples like Fourier transforms and neural networks to demonstrate complex concepts in a more digestible manner.
🧩 The Relevance and Storytelling in Math
The speaker explores what makes people engage with math, arguing that relevance to real-world applications is key. They discuss how connecting math to the world and the audience's interests can make it more appealing. However, the speaker suggests that there's another often-overlooked factor: storytelling. Using examples from their own YouTube content, they show how presenting math as a story, invoking emotions, and creating a sense of mystery can draw people in, even when the math problem at hand may not have immediate practical applications.
🎭 The Emotional Appeal of Mathematics
The speaker delves into the emotional and aesthetic aspects of mathematics, referencing the views of mathematician G. H. Hardy, who saw pure math as something to be appreciated for its beauty rather than its utility. They discuss how the narrative and emotional engagement with math can be as compelling as its practical applications. The speaker uses examples like block collisions on a frictionless surface and the probability of a tetrahedron enclosing the center of a sphere to illustrate how math can be as captivating as a good mystery novel, driving curiosity and engagement.
🌟 The Unexpected Utility of 'Useless' Math
The speaker reflects on the idea that even the most seemingly 'useless' math can have unforeseen practical applications. They recount how mathematicians like Hardy, who considered pure math to be without application, were eventually proven wrong as fields like number theory and relativity became foundational to technologies like cryptography and GPS. The speaker also shares an anecdote about how a problem on block collisions ended up being relevant to quantum computing, highlighting the unpredictable and often surprising ways in which mathematical concepts can intersect with real-world problems.
Mindmap
Keywords
💡Engagement
💡Fourier Transforms
💡Neural Networks
💡Visualization
💡Relevance
💡Storytelling
💡Complex Numbers
💡Pi (π)
💡Quantum Computing
💡Putnam Exam
💡Unexpected Connections
Highlights
The importance of engaging students with math by showing its relevance to understanding science and technology.
The challenge of maintaining engagement in a digital environment like YouTube, where viewers have countless entertainment options.
The use of visualizations and animations to make complex math topics like Fourier transforms more accessible.
The significance of Fourier transforms in various fields such as sound engineering, electrical engineering, and quantum mechanics.
The role of storytelling in mathematics, using the example of block collisions on a frictionless surface to create an engaging narrative.
The surprising connection between the math behind block collisions and quantum computing algorithms.
The concept that even 'useless' math can have unforeseen practical applications, as illustrated by the history of number theory and relativity.
The idea that math can be as engaging as fiction, appealing to emotions, wonder, and the desire to solve a mystery.
The popularity of math problems that appear on challenging exams like the Putnam competition, due to their perceived difficulty and intrigue.
The way successful math communicators use elements of story, character, and emotion to make math more engaging.
The importance of addressing the question 'When am I ever going to use this?' to make math more relatable and less intimidating.
The use of humor and wit in math communication, as demonstrated by channels like Stand-up Math.
The concept that math is not just about utility but also about beauty and the joy of discovery, as expressed by mathematicians like G.H. Hardy.
The unexpected ways in which pure math can become useful, as seen in the applications of number theory in cryptography.
The potential for math to provide a sense of pride, power, and accomplishment, similar to the benefits of physical exercise.
The role of math in revealing unexpected connections and its ability to shine a light on new areas of understanding.
The final takeaway that it's the intertwining of usefulness and story in math that makes it most compelling for engagement.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: